河南省安阳市殷都区2023年九年级中考一模数学试卷

试卷更新日期：2023-05-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一个不透明的袋子中装有2个红球、3个白球，每个球除颜色外都相同．从中任意摸出3个球，下列事件为必然事件的是（）

A、至少有1个球是红球 B、至少有1个球是白球 C、至少有2个球是红球 D、至少有2个球是白球

查看试题解析
3. 如图，在 $△ O A B$ 中，点 $C 、 D$ 分别在边 $O B 、 O A$ 的反向延长线上，且 $C D ∥ A B$ .若 $O C = 2$ ， $O B = 4$ ， $O D = 3$ ，则 $O A$ 的长为（）

A、4 B、6 C、8 D、 $10$

查看试题解析
4. 一元二次方程 $x^{2} - 3 x + 1 = 0$ 的根的情况（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定

查看试题解析
5. 如图是由6个相同的小正方体组成的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
6. 一个扇形的弧长是 $2 π$ ，半径是4，则该扇形的圆心角的度数是（）

A、 $45 °$ B、 $90 °$ C、 $120 °$ D、 $180 °$

查看试题解析
7. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形， $∠ B = 110 °$ ，则 $∠ A O C$ 的度数为（）

A、 $70 °$ B、 $110 °$ C、 $130 °$ D、 $140 °$

查看试题解析
8. 学校连续三年组织学生参加义务植树，第一年共植树 400 棵，第三年共植树 625 棵．设该校植树棵数的年平均增长率为 x，根据题意，下列方程正确的是（）

A、 $625 {(1 - x)}^{2} = 400$ B、 $400 {(1 + x)}^{2} = 625$ C、 $625 x^{2} = 400$ D、 $400 x^{2} = 625$

查看试题解析
9. 如图，在平面直角坐标系中， $△ O A B$ 的边 $O A$ 与x轴重合， $A B ⊥ x$ 轴，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过线段 $A B$ 的中点C.若 $△ O A B$ 的面积为8，则k的值为（）

A、4 B、 $- 4$ C、8 D、 $- 8$

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴的一个交点为 $(- 1 ， 0)$ ，对称轴为直线 $x = 1$ ，下列结论：① $a c > 0$ ；② $2 a + b = 0$ ；③ $a + b + c > 0$ ；④当 $x > 0$ 时，y随x的增大而减小；⑤关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两根分别是-1和3，其中正确的结论有（）

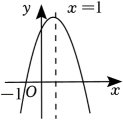A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 式子 $2 c o s 30 ° - t a n 45 °$ 的值是.

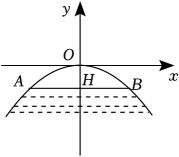
查看试题解析
12. 已知点 $A （ 2 ， m ）$ 与 $B （ - 2 ， 5 ）$ 关于原点对称，则m=.

查看试题解析
13. 如图所示，拱桥的形状是抛物线，其函数关系式为 $y = - \frac{1}{16} x^{2}$ ，当水面离桥顶的高度 $O H$ 为 $4 m$ 时，水面的宽度AB为m.

查看试题解析
14. 如图，将 $△ A O B$ 按如图方式放在平面直角坐标系中，其中 $∠ O A B = 90 °$ ， $∠ B = 30 °$ ，顶点A的坐标为 $(- 1 ， 0)$ ，将 $△ A O B$ 绕原点O顺时针旋转 $60 °$ 得到 $△ O A^{'} B^{'}$ ，则点 $B^{'}$ 的坐标为.

查看试题解析
15. 如图，扇形纸片 $A O B$ 的半径为2，沿 $A B$ 折叠扇形纸片，点O恰好落在 $\overset{⌢}{A B}$ 上的点C处，图中阴影部分的面积为.

查看试题解析

三、解答题

16. 如图，正比例函数 $y = 3 x$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $A (- 2 ， a)$ 、B两点.

(1)、求反比例函数的表达式；

(2)、结合图象直接写出不等式 $\frac{k}{x} \leq 3 x$ 的解集.

查看试题解析
17. 为深入学习贯彻党的二十大精神，某学校决定举办“青春心向党，奋进新征程”主题演讲比赛，该校九年级一班有 $1$ 男 $3$ 女共 $4$ 名学生报名参加演讲比赛.

(1)、若从报名的 $4$ 名学生中随机选 $1$ 名，则所选的这名学生是女生的概率是；

(2)、若从报名的 $4$ 名学生中随机选 $2$ 名，用画树状图或列表的方法，求这 $2$ 名学生都是女生的概率.

查看试题解析
18. 如图，O是直线 $M N$ 上一点， $∠ A O B = 90 °$ ，过点A作 $A C ⊥ M N$ 于点C，过点B作 $B D ⊥ M N$ 于点D.

(1)、求证： $△ A O C ∽ △ O B D$ ；

(2)、若 $O A = 5$ ， $O C = O D = 3$ ，求 $B D$ 的长.

查看试题解析
19. 某校九年级数学项目化学习主题是“测量物体高度”.小明所在小组想测量中国文字博物馆门口字坊 $A B$ 的高度.如图，在C处测得字坊顶端B的仰角为 $37 °$ ，然后沿 $C A$ 方向前进 $6.3 m$ 到达点D处，测得字坊顶端B的仰角为 $45 °$ ，求字坊 $A B$ 的高度.(结果精确到 $0.1 m$ ，参考数据：s $i n 37 ° \approx$ $\frac{3}{5}$ ， $c o s 37 ° \approx$ $\frac{4}{5}$ ， $t a n 37 ° \approx$ $\frac{3}{4}$ ， $\sqrt{2}$ $\approx 1.41$ )

查看试题解析
20. 如图， $△ A B C$ 内接于 $⊙ O$ ， $A B$ 、 $C D$ 是 $⊙ O$ 的直径，E是 $D A$ 长线上一点，且 $∠ C E D = ∠ C A B$ .

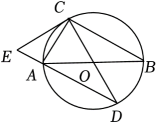(1)、判断 $C E$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $D E = 3 \sqrt{5}$ ， $t a n B = \frac{1}{2}$ ，求线段 $C E$ 的长.

查看试题解析
21. 兔年来临之际，某商店销售一种小兔子毛绒玩具，每件进价为30元，经过试销发现，该玩具每天的销售量y（件）与销售单价x（元）之间满足如下关系： $y = - x + 60$

(1)、求该商店销售这种毛绒玩具每天获得的利润w（元）与x之间的函数关系式；

(2)、若商店销售这种毛绒玩具每天想获得200元的利润，且最大限度让利给顾客，则销售单价应定为多少元？

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点A，B $(1 ， 0)$ ，与y轴交于点C，且 $O A = O C$ .

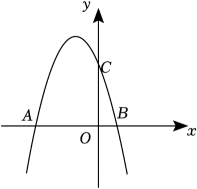(1)、求抛物线的解析式及顶点坐标；

(2)、当 $k \leq x < 0$ ，且 $k < - 1$ 时，y的最大值和最小值分别为m，n，且 $m + n = - 1$ ，求k的值.

查看试题解析
23. 九年级一班同学在数学老师的指导下，以“等腰三角形的旋转”为主题，开展数学探究活动.

(1)、操作探究：如图1， $△ O A B$ 为等腰三角形， $O A = O B ， ∠ A O B = 60 °$ ，将 $△ O A B$ 绕点O旋转 $180 °$ ，得到 $△ O D E$ ，连接 $A E$ ， F是AE的中点，连接 $O F$ ，则 $∠ B A E =$ °， $O F$ 与 $D E$ 的数量关系是；

(2)、迁移探究：如图2，（1）中的其他条件不变，当 $△ O A B$ 绕点O逆时针旋转，点D正好落在 $∠ A O B$ 的角平分线上，得到 $△ O D E$ ，求出此时 $∠ B A E$ 的度数及 $O F$ 与 $D E$ 的数量关系；

(3)、拓展应用：如图3，在等腰三角形 $△ O A B$ 中， $O A = O B = 4$ ， $∠ A O B = 90 °$ .将 $△ O A B$ 绕点O旋转，得到 $△ O D E$ ，连接 $A E$ ， F是 $A E$ 的中点，连接 $O F$ .当 $∠ E A B = 15 °$ 时，请直接写出 $O F$ 的长.

查看试题解析