陕西省铜川市2023届高三理数二模试卷
试卷更新日期:2023-05-04 类型:高考模拟
一、单选题
-
1. 若全集 , , , 则( ).A、{2} B、{3} C、{4} D、2. 已知复数 , 满足 , , 则( )A、 B、 C、 D、63. 执行下面的程序框图,则输出S的值为( )
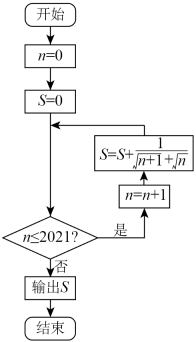 A、 B、 C、 D、4. 如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III.在整个图形中随机取一点,此点取自I,II,III的概率分别记为p1 , p2 , p3 , 则
A、 B、 C、 D、4. 如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III.在整个图形中随机取一点,此点取自I,II,III的概率分别记为p1 , p2 , p3 , 则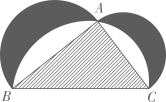 A、p1=p2 B、p1=p3 C、p2=p3 D、p1=p2+p35. 命题:“ , ”的否定是( )A、 , B、 , C、 , D、 ,6. 已知 , 则( )A、 B、 C、 D、7. 现有甲、乙两组数据,每组数据均由六个数组成,其中甲组数据的平均数为 , 方差为 , 乙组数据的平均数为 , 方差为 . 若将这两组数据混合成一组,则新的一组数据的方差为( )A、3.5 B、4 C、4.5 D、58. 等比数列满足 , 设数列的前项和为 , 则=( )A、-11 B、-8 C、5 D、119. 如图,在的边、上分别取点、 , 使 , , 与交于点 , 若 , , 则的值为
A、p1=p2 B、p1=p3 C、p2=p3 D、p1=p2+p35. 命题:“ , ”的否定是( )A、 , B、 , C、 , D、 ,6. 已知 , 则( )A、 B、 C、 D、7. 现有甲、乙两组数据,每组数据均由六个数组成,其中甲组数据的平均数为 , 方差为 , 乙组数据的平均数为 , 方差为 . 若将这两组数据混合成一组,则新的一组数据的方差为( )A、3.5 B、4 C、4.5 D、58. 等比数列满足 , 设数列的前项和为 , 则=( )A、-11 B、-8 C、5 D、119. 如图,在的边、上分别取点、 , 使 , , 与交于点 , 若 , , 则的值为 A、 B、 C、 D、610. 已知 , 分别是双曲线的左、右焦点,直线l经过且与C左支交于P,Q两点,P在以为直径的圆上, , 则C的离心率是( )A、 B、 C、 D、11. 已知函数在一个周期内的函数图象如图所示.若方程在区间有两个不同的实数解 , , 则
A、 B、 C、 D、610. 已知 , 分别是双曲线的左、右焦点,直线l经过且与C左支交于P,Q两点,P在以为直径的圆上, , 则C的离心率是( )A、 B、 C、 D、11. 已知函数在一个周期内的函数图象如图所示.若方程在区间有两个不同的实数解 , , 则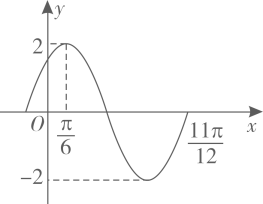 A、 B、 C、 D、或12. 在四棱锥中,底面为菱形, , 平面 , , 为线段的中点,为线段上的动点,则下列结论错误的是( )A、平面平面 B、三棱锥的体积为 C、与平面所成角的最小值为 D、与所成角的余弦值为
A、 B、 C、 D、或12. 在四棱锥中,底面为菱形, , 平面 , , 为线段的中点,为线段上的动点,则下列结论错误的是( )A、平面平面 B、三棱锥的体积为 C、与平面所成角的最小值为 D、与所成角的余弦值为二、填空题
-
13. 将四大名著各分一本给甲、乙、丙、丁四人就读,A、、、四位旁观者预测分配结果,A说:“甲读《西游记》,乙读《红楼梦》”;说:“甲读《水浒传》,丙读《三国演义》”;说:“乙读《水浒传》,丙读《西游记》”;说:“乙读《西游记》,丁读《三国演义》”.若已知四位旁观者每人预测的两句话中,都是有且只有一句是真的,则可推断丁读的名著是.14. 已知函数 , 若 , 则函数的值域为.15. 已知数列的前项和为 , 且点总在直线上,则数列的前项和.16. 已知椭圆的左、右焦点分别为 , , 直线与椭圆交于 , 两点(其中点在点的左侧),记面积为 , 则下列四个结论正确的是.
① ②时,
③的最大值为 ④当时,点的横坐标为
三、解答题
-
17. 在中,角所对的边分别为 , .(1)、证明:;(2)、若 , 当角取得最大值时,求的面积.18. 如图,在斜三棱柱中,底面ABC是边长为2的正三角形, , 侧棱AD与底面ABC所成角为60°.
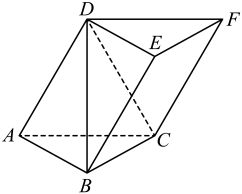 (1)、求证:四边形BCFE为矩形;(2)、求平面DBC与平面BCFE夹角的余弦值.19. 为进一步巩固提升全国文明城市,加速推行垃圾分类制度,铜川市推出了两套方案,并分别在、两个大型居民小区内试行.方案一:进行广泛的宣传活动,向小区居民和社会各界宣传垃圾分类的意义,讲解分类垃圾桶的使用方式,垃圾投放时间等,定期召开垃圾分类会议和知识宣传教育活动;方案二:在小区内设立智能化分类垃圾桶,智能垃圾桶操作简单,居民可以通过手机进行自动登录、称重、积分等一系列操作.并建立激励机制,比如,垃圾分类换积分兑换礼品等,以激发带动居民参与垃圾分类的热情.经过一段时间试行之后,在这两个小区内各随机抽取了100名居民进行问卷调查,记录他们对试行方案的满意度得分(满分100分),将数据分成6组: , , , , , , 并整理得到如图所示的频率分布直方图:
(1)、求证:四边形BCFE为矩形;(2)、求平面DBC与平面BCFE夹角的余弦值.19. 为进一步巩固提升全国文明城市,加速推行垃圾分类制度,铜川市推出了两套方案,并分别在、两个大型居民小区内试行.方案一:进行广泛的宣传活动,向小区居民和社会各界宣传垃圾分类的意义,讲解分类垃圾桶的使用方式,垃圾投放时间等,定期召开垃圾分类会议和知识宣传教育活动;方案二:在小区内设立智能化分类垃圾桶,智能垃圾桶操作简单,居民可以通过手机进行自动登录、称重、积分等一系列操作.并建立激励机制,比如,垃圾分类换积分兑换礼品等,以激发带动居民参与垃圾分类的热情.经过一段时间试行之后,在这两个小区内各随机抽取了100名居民进行问卷调查,记录他们对试行方案的满意度得分(满分100分),将数据分成6组: , , , , , , 并整理得到如图所示的频率分布直方图: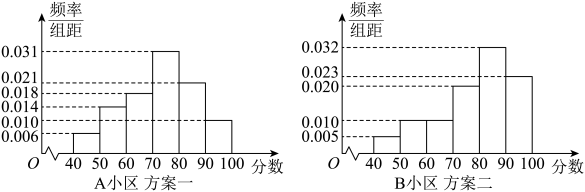 (1)、请通过频率分布直方图分别估计两种方案满意度的平均得分,判断哪种方案的垃圾分类推广措施更受居民欢迎(同一组中的数据用该组中间的中点值作代表);(2)、以样本频率估计概率,若满意度得分不低于70分认为居民赞成推行此方案,低于70分认为居民不赞成推行此方案,规定小区居民赞成率不低于才可在该小区继续推行该方案,判断两小区哪个小区可继续推行方案?(3)、根据(2)中结果,从可继续推行方案的小区内随机抽取5个人,用表示赞成该小区推行方案的人数,求的分布列及数学期望.20. 已知点F为抛物线E:()的焦点,点P(−3,2), , 若过点P作直线与抛物线E顺次交于A,B两点,过点A作斜率为1的直线与抛物线的另一个交点为点C.(1)、求抛物线E的标准方程;(2)、求证:直线BC过定点;(3)、若直线BC所过定点为点Q,△QAB,△PBC的面积分别为S1 , S2 , 求的取值范围
(1)、请通过频率分布直方图分别估计两种方案满意度的平均得分,判断哪种方案的垃圾分类推广措施更受居民欢迎(同一组中的数据用该组中间的中点值作代表);(2)、以样本频率估计概率,若满意度得分不低于70分认为居民赞成推行此方案,低于70分认为居民不赞成推行此方案,规定小区居民赞成率不低于才可在该小区继续推行该方案,判断两小区哪个小区可继续推行方案?(3)、根据(2)中结果,从可继续推行方案的小区内随机抽取5个人,用表示赞成该小区推行方案的人数,求的分布列及数学期望.20. 已知点F为抛物线E:()的焦点,点P(−3,2), , 若过点P作直线与抛物线E顺次交于A,B两点,过点A作斜率为1的直线与抛物线的另一个交点为点C.(1)、求抛物线E的标准方程;(2)、求证:直线BC过定点;(3)、若直线BC所过定点为点Q,△QAB,△PBC的面积分别为S1 , S2 , 求的取值范围