陕西省安康市2023届高三理数三模试卷

试卷更新日期：2023-05-04 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {(x ， y) | y = x^{2}} ， B = {(x ， y) | y = x}$ ，则 $A ∩ B =$ （）

A、 ${0 ， 1}$ B、 ${(0 ， 0)}$ C、 ${(1 ， 1)}$ D、 ${(0 ， 0) ， (1 ， 1)}$

查看试题解析
2. 若复数 $z = a + b i (a ， b \in R)$ 满足 $\frac{z}{2 + i}$ 为纯虚数，则 $\frac{b}{a} =$ （）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
3. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{3} + a_{4} = 4$ ，则 $S_{6} =$ （）

A、6 B、12 C、18 D、24

查看试题解析
4. 已知向量 $\vec{a} = (2 ， 1)$ ， $\vec{b} = (1 ， x)$ ，若 $2 \vec{a} - \vec{b}$ 与 $\vec{b}$ 共线，则 $| \vec{b} | =$ （）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{5}{4}$ C、 $\sqrt{5}$ D、5

查看试题解析
5. 党的二十大报告提出全面推进乡村振兴.为振兴乡村经济，某市一知名电商平台决定为乡村的特色产品开设直播带货专场.该特色产品的热卖黄金时段为2023年3月1至5月31日，为了解直播的效果和关注度，该电商平台统计了已直播的2023年3月1日至3月5日时段的相关数据，这5天的第 $x$ 天到该电商平台专营店购物人数 $y$ （单位：万人）的数据如下表：
日期
3月1日
3月2日
3月3日
3月4日
3月5日
第x天
1
2
3
4
5
人数y（单位：万人）
75
84
93
98
100
依据表中的统计数据，经计算得 $y$ 与 $x$ 的线性回归方程为 $\hat{y} = 6.4 x + a$ .请预测从2023年3月1日起的第58天到该专营店购物的人数（单位：万人）为（）

A、440 B、441 C、442 D、443

查看试题解析
6. 羽毛球运动是一项全民喜爱的体育运动，标准的羽毛球由16根羽毛固定在球托上，测得每根羽毛在球托之外的长为 $6 c m$ ，球托之外由羽毛围成的部分可看成一个圆台的侧面，测得顶端所围成圆的直径是 $6 c m$ ，底部所围成圆的直径是 $2 c m$ ，据此可估算得球托之外羽毛所在曲面的展开图的圆心角为（）

A、 $\frac{π}{3}$ B、 $\frac{π}{2}$ C、 $\frac{2 π}{3}$ D、 $π$

查看试题解析
7. 在 ${(\frac{2}{x} - x)}^{7}$ 的展开式中，下列说法正确的是（）

A、所有项的二项式系数和为1 B、第4项和第5项的二项式系数最大 C、所有项的系数和为128 D、第4项的系数最大

查看试题解析
8. 已知方程 $(x^{2} - m x + 27) (x^{2} - n x + 27) = 0$ 的四个根组成以1为首项的等比数列，则 $| m - n | =$ （）

A、8 B、12 C、16 D、20

查看试题解析
9. 已知正三棱锥 $P - A B C$ 的顶点都在球 $O$ 的球面上，其侧棱与底面所成角为 $\frac{π}{3}$ ，且 $P A = 2 \sqrt{3}$ ，则球 $O$ 的表面积为（）

A、 $8 π$ B、 $12 π$ C、 $16 π$ D、 $18 π$

查看试题解析
10. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左，右焦点分别为 $F_{1}$ ， $F_{2}$ ， $P$ 为椭圆 $C$ 上一点， $∠ F_{1} P F_{2} = 60 °$ ，点 $F_{2}$ 到直线 $P F_{1}$ 的距离为 $\frac{\sqrt{3}}{3} a$ ，则椭圆 $C$ 的离心率为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{6}}{3}$ D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
11. 定义在 $R$ 上的函数 $f (x)$ 满足 $f (2 - x) = f (x)$ ，且 $f (x + 2) - 1$ 为奇函数，则 $\sum_{k = 1}^{2023} f (k)$ （）

A、-2023 B、-2022 C、2022 D、2023

查看试题解析
12. 若 $\sqrt{1 + 2 a} = e^{b} = \frac{1}{1 - c} = 1.01$ ，则（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析

二、填空题

13. 已知 $x ， y$ 满足约束条件 ${\begin{array}{l} x > 0 \\ x - 2 y \leq - 2 \\ x + y \leq 7 \end{array}$ ，则 $z = x - y$ 的最大值是.

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} 4^{x} ， x \leq 0 \\ f (x - 1) ， x > 0 \end{array}$ ，则 $f (l o g_{2} 3) =$ .

查看试题解析
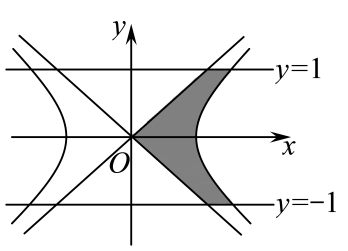
15. 已知函数 $f (x) = c o s ω x (ω > 0)$ 的图象关于点 $(\frac{π}{2} ， 0)$ 对称，且在区间 $[0 ， \frac{π}{8}]$ 单调，则 $ω$ 的一个取值是.

查看试题解析
16. 《九章算术》中记载了我国古代数学家祖暅在计算球的体积时使用的一个原理：“幂势既同，则积不容异”，此即祖暅原理，其含义为：两个同高的几何体，如在等高处的截面的面积恒相等，则它们的体积相等.已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点到渐近线的距离记为 $d$ ，双曲线 $C$ 的两条渐近线与直线 $y = 1$ ， $y = - 1$ 以及双曲线 $C$ 的右支围成的图形（如图中阴影部分所示）绕 $y$ 轴旋转一周所得几何体的体积为 $\frac{\sqrt{6}}{3} d c π$ （其中 $c^{2} = a^{2} + b^{2}$ ），则双曲线 $C$ 的离心率为.

查看试题解析

三、解答题

17. 已知 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，且 $a < c$ ， $s i n (\frac{π}{3} - A) c o s (\frac{π}{6} + A) = \frac{1}{4}$ .

(1)、求 $A$ ；

(2)、若 $b = \sqrt{3}$ ， $a s i n A + c s i n C = 4 \sqrt{3} s i n B$ ，求 $△ A B C$ 的面积.

查看试题解析
18. 某市为了传承发展中华优秀传统文化，组织该市中学生进行了一次文化知识有奖竞赛，竞赛奖励规则如下：得分在 $[70 ， 80)$ 内的学生获三等奖，得分在 $[80 ， 90)$ 内的学生获二等奖，得分在 $[90 ， 100]$ 内的学生获一等奖，其他学生不得奖.为了解学生对相关知识的掌握情况，随机抽取100名学生的竞赛成绩，并以此为样本绘制了如图所示的样本频率分布直方图.
附：若随机变量 $X$ 服从正态分布 $N (μ ， σ^{2})$ ，则 $P (μ - σ \leq X \leq μ + σ) \approx 0.6827$ ， $P (μ - 2 σ \leq X \leq μ + 2 σ) \approx 0.9545$ ， $P (μ - 3 σ \leq X \leq μ + 3 σ) \approx 0.9973$ .

(1)、现从该样本中随机抽取2名学生的竞赛成绩，求这2名学生中恰有1名学生获奖的概率；

(2)、估计这100名学生的竞赛成绩的平均数（同一组中的数据用该组区间的中点值作代表）；

(3)、若该市共有10000名学生参加了竞赛，所有参赛学生的成绩 $X$ 近似服从正态分布 $N (μ ， σ^{2})$ ，其中 $σ \approx 14$ ， $μ$ 为样本平均数的估计值，试估计参赛学生中成绩超过78分的学生人数（结果四舍五入到整数）.

查看试题解析
19. 如图1，四边形 $A B C D$ 是梯形， $A B / / C D$ ， $A D = D C = C B = \frac{1}{2} A B = 4$ ， $M$ 是 $A B$ 的中点，将 $△ A D M$ 沿 $D M$ 折起至 $△ A^{^{'}} D M$ ，如图2，点 $N$ 在线段 $A^{'} C$ 上.

(1)、若 $N$ 是 $A^{'} C$ 的中点，证明：平面 $D M N ⊥$ 平面 $A^{'} B C$ ；

(2)、若 $A^{^{'}} C = 2 \sqrt{6}$ ，二面角 $C - D M - N$ 的余弦值为 $\frac{\sqrt{5}}{5}$ ，求 $\frac{A^{^{'}} N}{N C}$ 的值.

查看试题解析
20. 已知函数 $f (x) = m e^{x} + \frac{l n x - 2}{x} + 1$ .

(1)、若 $m = 0$ ，求函数 $f (x)$ 的极值；

(2)、若 $f (x) < 0$ 恒成立，求 $m$ 的取值范围.

查看试题解析
21. 已知抛物线 $C ： y^{2} = 2 p x$ 的焦点为 $F (1 ， 0)$ .

(1)、求抛物线 $C$ 的方程；

(2)、过点 $F$ 的直线 $l$ 与抛物线 $C$ 交于 $A ， B$ 两点， $M$ 为抛物线 $C$ 上的点，且 $A M ⊥ B M$ ， $M F ⊥ A B$ ，求 $△ A B M$ 的面积.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，已知直线 $l$ 的参数方程为 ${\begin{array}{l} x = 2 (t - 2 \sqrt{2}) \\ y = t \end{array}$ （ $t$ 为参数）.以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ^{2} (1 + 3 s i n^{2} θ) = 4$ .

(1)、求直线 $l$ 的普通方程与曲线 $C$ 的直角坐标方程；

(2)、若射线 $θ = β$ （其中 $β \in (0 ， π)$ ，且 $t a n β = - \frac{1}{2}$ ， $ρ \geq 0$ ）与曲线 $C$ 在 $x$ 轴上方交于点 $M$ ，与直线 $l$ 交于点 $N$ ，求 $| M N |$ .

查看试题解析
23. 已知函数 $f (x) = | 2 x + 2 | + | x - 3 |$ .

(1)、求不等式 $f (x) \leq 5$ 的解集；

(2)、若 $\forall x \in R$ ， $| a^{2} - 3 a | \leq f (x)$ ，求 $a$ 的取值范围.

查看试题解析

日期	3月1日	3月2日	3月3日	3月4日	3月5日
第x天	1	2	3	4	5
人数y（单位：万人）	75	84	93	98	100