黑龙江大庆市2023届高三数学三模试卷

试卷更新日期：2023-05-04 类型：高考模拟

进入出卷网下载

一、单选题

1. 复数 $z = \frac{2 + i}{1 + 3 i}$ 的虚部是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2} i$ D、 $- \frac{1}{2} i$

查看试题解析
2. 若集合 $A = {x | l o g_{2} x < 2}$ ， $B = {x | x \geq 2}$ ，则 $A ∩ B =$ （）

A、 $[2 ， 4]$ B、 $(2 ， 4]$ C、 $\emptyset$ D、 $[2 ， 4)$

查看试题解析
3. 定义 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，已知数列 ${a_{n}}$ 为等比数列，且 $a_{3} = 1$ ， $| \begin{array}{l} a_{6} & 8 \\ 8 & a_{8} \end{array} | = 0$ ，则 $a_{7} =$ （）

A、4 B、±4 C、8 D、±8

查看试题解析
4. 已知向量 $\vec{a} = (s i n α ， 3)$ ， $\vec{b} = (c o s α ， 1)$ ，若 $\vec{a} / / \vec{b}$ ，则 $\frac{s i n 2 α}{c o s^{2} α} =$ （）

A、3 B、6 C、 $- 3$ D、 $- 6$

查看试题解析
5. 已知直线 $l$ 是圆 $C ：$ ${(x - 2)}^{2} + {(y - 1)}^{2} = 1$ 的切线，并且点 $B (3 ， 4)$ 到直线 $l$ 的距离是2，这样的直线 $l$ 有（）

A、1条 B、2条 C、3条 D、4条

查看试题解析
6. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = B C = 4$ ， $A A_{1} = 1$ ， $M$ 为 $A_{1} B_{1}$ 的中点， $P$ 为底面 $A B C D$ 上一点，若直线 $D_{1} P$ 与平面 $B M C_{1}$ 没有交点，则 $△ D_{1} D P$ 面积的最小值为（）

A、 $1$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{4 \sqrt{5}}{5}$

查看试题解析
7. 函数 $f (x) = \frac{e^{x} (2 x - 1)}{x - 1}$ ，则方程 $f (x) = 4 e$ 解的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 已知 $a = e^{- 3}$ ， $b = l n 1.02$ ， $c = s i n 0.04$ ，则（）

A、 $a < b < c$ B、 $b < c < a$ C、 $c < b < a$ D、 $b < a < c$

查看试题解析

二、多选题

9. 已知事件A，B满足 $P (A) = 0.3$ ， $P (B) = 0.6$ ，则（）

A、若 $A ⊆ B$ ，则 $P (A B) = 0.18$ B、若A与B互斥，则 $P (A + B) = 0.9$ C、若 $P (A | B) = 0.1$ ，则A与B相互独立 D、若A与B相互独立，则 $P (A \bar{B}) = 0.12$

查看试题解析
10. 筒车是我国古代发明的一种水利灌溉工具，既经济又环保，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1.假定在水流量稳定的情况下，筒车上的每一个盛水筒都做匀速圆周运动.为研究筒车的运动情况，将筒车抽象为一个以原点为圆心，R为半径的圆，某盛水筒抽象为圆上的点P，如图2.设筒车按逆时针方向每旋转一周用时100秒，当点P位于初始点 $P_{0} (2 ， - 2 \sqrt{3})$ 时记为 $t = 0$ 秒，在筒车旋转t秒的过程中，点 $P (x ， y)$ 的纵坐标满足 $y = f (t) = R s i n (ω t + φ) (t \geq 0 ， ω > 0 ， | φ | < \frac{π}{2})$ ，则下列叙述正确的是（）

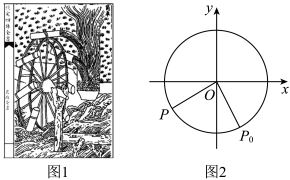A、筒车转动的角速度 $ω = \frac{π}{50}$ B、当 $t = 75$ 秒时，点P的纵坐标为-2 C、当 $t = 75$ 秒时，点P和初始点 $P_{0}$ 的距离为4 D、当 $0 < t \leq 30$ 秒时，点P距离x轴的最大值为4

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别是 $F_{1}$ ， $F_{2}$ ，渐近线方程为 $2 x \pm y = 0$ ， M为双曲线E上任意一点， $M N$ 平分 $∠ F_{1} M F_{2}$ ，且 $\vec{F_{1} N} \cdot \vec{M N} = 0$ ， $| O N | = 2$ ，则（）

A、双曲线的离心率为 $\sqrt{5}$ B、双曲线的标准方程为 $x^{2} - \frac{y^{2}}{4} = 1$ C、点M到两条渐近线的距离之积为 $\frac{16}{5}$ D、若直线 $M F_{1}$ 与双曲线E的另一个交点为P，Q为 $M P$ 的中点，则 $k_{O Q} \times k_{P M} = 4$

查看试题解析
12. 勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体，若用棱长为4的正四面体 $A B C D$ 作勒洛四面体，如图，则下列说法正确的是（）

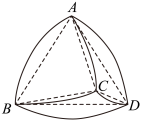A、平面 $A B C$ 截勒洛四面体所得截面的面积为 $8 π - 8 \sqrt{3}$ B、记勒洛四面体上以C，D为球心的两球球面交线为弧 $A B$ ，则其长度为 $\frac{4 π}{3}$ C、该勒洛四面体表面上任意两点间距离的最大值为4 D、该勒洛四面体能够容纳的最大球的半径为 $4 - \sqrt{6}$

查看试题解析

三、填空题

13. 曲线 $f (x) = l n x + \frac{2}{x}$ 在点 $(1 ， 2)$ 处的切线方程为.

查看试题解析
14. 某校学生参与“保护地球”知识问答活动，满分20分，根据学生的作答成绩绘制的频率分布直方图如图所示，请据此估计学生成绩的第60百分位数为．

查看试题解析
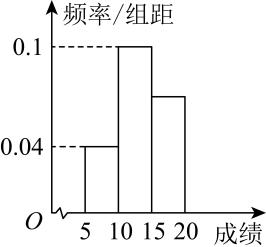15. 已知函数 $f (x) = \frac{3 e^{x}}{1 + e^{x}}$ ，则 $f (x) + f (- x) =$ ；若 $\forall x \in (0 ， + \infty)$ ，不等式 $f (4 - a x) + f (x^{2}) \geq 3$ 恒成立，则实数a的取值范围是．

查看试题解析
16. 古希腊数学家阿波罗尼奥斯与欧几里得、阿基米德齐名，他的著作《圆锥曲线论》是古代数学光辉的科学成果．他发现“平面内到两个定点A，B的距离之比为定值 $λ$ （ $λ > 0$ 且 $λ \neq 1$ ）的点的轨迹是圆”，人们将这样的圆称为阿波罗尼斯圆，简称阿氏圆．在平面直角坐标系中，已知 $A (0 ， 1)$ ， $B (0 ， 2)$ ， $C (- \sqrt{2} ， 2)$ ， Q为抛物线 $y^{2} = 4 \sqrt{2} x$ 上的动点，点Q在直线 $x = - \sqrt{2}$ 上的射影为H，M为圆 ${(x + \sqrt{2})}^{2} + y^{2} = 2$ 上的动点，若点P的轨迹是到A，B两点的距离之比为 $\frac{\sqrt{2}}{2}$ 的阿氏圆，则 $\frac{\sqrt{2}}{2} | M C | + | Q H | + | Q M |$ 的最小值为．

查看试题解析

四、解答题

17. 在 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，已知 $\sqrt{3} b = a (\sqrt{3} c o s C - s i n C)$ .

(1)、求 $A$ ；

(2)、若 $a = 8$ ， $△ A B C$ 的内切圆半径为 $\sqrt{3}$ ，求 $△ A B C$ 的周长.

查看试题解析
18. 已知数列 ${a_{n}}$ 满足 $a_{1} + 3 a_{2} + ⋯ + (2 n - 1) a_{n} = n$ ．

(1)、证明： ${\frac{1}{a_{n}}}$ 是一个等差数列；

(2)、已知 $c_{n} = {\begin{array}{l} \frac{1}{19 a_{n}} ， n 为奇数 \\ a_{n} a_{n + 2} ， n 为偶数 \end{array}$ ，求数列 ${c_{n}}$ 的前 $2 n$ 项和 $S_{2 n}$ ．

查看试题解析
19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = B C = 4$ ， D是 $A C$ 中点， $∠ A A_{1} B_{1} = ∠ B_{1} B C$ ．

(1)、证明： $A A_{1} ⊥ A C$ ；

(2)、若 $B B_{1} ⊥ A B$ ， $∠ A B C = 60 °$ ，且三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的体积为 $12 \sqrt{3}$ ，求二面角 $B - B_{1} D - C_{1}$ 的余弦值．

查看试题解析
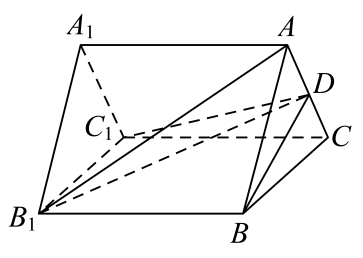20. 天宫空间站是我国建成的国家级太空实验室，由天和核心舱、问天实验舱和梦天实验舱组成，已经开启长期有人驻留模式，结合空间站的相关知识，某职业学校的老师设计了以空间站为主题的编程训练，训练内容由“太空发射”、“自定义漫游”、“全尺寸太阳能”、“空间运输”等10个相互独立的编程题目组成，训练要求每个学生必须选择两个不同的题目进行编程练习，并且学生间的选择互不影响，老师将班级学生分成四组，指定甲、乙、丙、丁为组长.

(1)、求甲、乙、丙、丁这四个人中至少有一人选择“太空发射”的概率；

(2)、记X为这四个人中选择“太空发射”的人数，求X的分布列及数学期望；

(3)、如果班级有n个学生参与编程训练（其中n是能被5整除的正整数），则这n个学生中选择“太空发射”的人数最有可能是多少人？

查看试题解析
21. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为e，且过 $(2 ， 0)$ ， $(1 ， e)$ 两点.

(1)、求椭圆E的方程；

(2)、若经过 $M (1 ， 0)$ 有两条直线 $l_{1}$ ， $l_{2}$ ，它们的斜率互为倒数， $l_{1}$ 与椭圆E交于A，B两点， $l_{2}$ 与椭圆E交于C，D两点，P，Q分别是 $A B$ ， $C D$ 的中点.试探究： $△ O P Q$ 与 $△ M P Q$ 的面积之比是否为定值？若是，请求出此定值；若不是，请说明理由.

查看试题解析
22. 已知函数 $f (x) = e^{a x} (l n x + b)$ ，其中 $a$ ， $b \in R$ ．

(1)、若 $\forall b \in R$ ， $f (x)$ 有且仅有一个极值点，求实数 $a$ 的取值范围；

(2)、是否存在 $a$ ， $b \in R$ ， $x_{0} > 0$ ，使得 $x_{0}$ 是 $f (x)$ 的极值点，且满足 $f (x_{0}) \in [- e ， 0]$ ，若存在，求出所有这样的 $a$ ， $b$ ；若不存在，请说明理由．

查看试题解析