广西壮族自治区玉林市2023届高三理数教学质量检测试卷
试卷更新日期:2023-05-04 类型:高考模拟
一、单选题
-
1. 已知复数z对应的向量为(O为坐标原点),与实轴正向的夹角为120°,且复数z的模为2,则复数z为( )A、1+i B、2 C、 D、-1+i2. 设集合 , 则选项正确的是( )A、 B、 C、 D、3. 已知且 , , 则p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 为了发展学生的兴趣和个性特长,培养全面发展的人才.某学校在不加重学生负担的前提下.提供个性、全面的选修课程.为了解学生对于选修课《学生领导力的开发》的选择意愿情况,对部分高二学生进行了抽样调查,制作出如图所示的两个等高条形图,根据条形图,下列结论正确的是( )
 A、样本中不愿意选该门课的人数较多 B、样本中男生人数多于女生人数 C、样本中女生人数多于男生人数 D、该等高条形图无法确定样本中男生人数是否多于女生人数5. 设 , 为两个不同的平面,则的一个充分条件是( )A、内有无数条直线与平行 B、 , 平行于同一个平面 C、 , 平行于同一条直线 D、 , 垂直于同一个平面6. 2022年神舟接力腾飞,中国空间站全面建成,我们的“太空之家”遨游苍穹.太空中飞船与空间站的对接,需要经过多次变轨.某飞船升空后的初始运行轨道是以地球的中心为一个焦点的椭圆,其远地点(长轴端点中离地面最远的点)距地面 , 近地点(长轴端点中离地面最近的点)距地面 , 地球的半径为 , 则该椭圆的短轴长为( )A、 B、 C、 D、7. 已知 , 若的展开式的第2项的二项式系数与第4项的二项式系数相等,则=( )A、32 B、64 C、128 D、2568. 已知等比数列的前n项和为 , 若 , 则( )A、12 B、36 C、31 D、339. 如图,动点P从点M出发,按照路径运动,四边形ABCD是边长为2的正方形,弧DM以A为圆心,AD为半径,设点P的运动路程为x,的面积为y,则函数的图象大致是( )
A、样本中不愿意选该门课的人数较多 B、样本中男生人数多于女生人数 C、样本中女生人数多于男生人数 D、该等高条形图无法确定样本中男生人数是否多于女生人数5. 设 , 为两个不同的平面,则的一个充分条件是( )A、内有无数条直线与平行 B、 , 平行于同一个平面 C、 , 平行于同一条直线 D、 , 垂直于同一个平面6. 2022年神舟接力腾飞,中国空间站全面建成,我们的“太空之家”遨游苍穹.太空中飞船与空间站的对接,需要经过多次变轨.某飞船升空后的初始运行轨道是以地球的中心为一个焦点的椭圆,其远地点(长轴端点中离地面最远的点)距地面 , 近地点(长轴端点中离地面最近的点)距地面 , 地球的半径为 , 则该椭圆的短轴长为( )A、 B、 C、 D、7. 已知 , 若的展开式的第2项的二项式系数与第4项的二项式系数相等,则=( )A、32 B、64 C、128 D、2568. 已知等比数列的前n项和为 , 若 , 则( )A、12 B、36 C、31 D、339. 如图,动点P从点M出发,按照路径运动,四边形ABCD是边长为2的正方形,弧DM以A为圆心,AD为半径,设点P的运动路程为x,的面积为y,则函数的图象大致是( ) A、
A、 B、
B、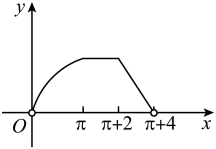 C、
C、 D、
D、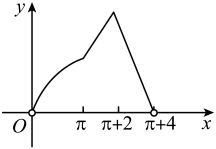 10. 已知函数在处取得最大值,则( )A、 B、 C、 D、11. 设点 , , 圆: , 点满足 , 设点的轨迹为 , 与交于点 , , 为直线上一点(为坐标原点),则( )A、4 B、 C、2 D、12. 在正四棱柱中, , , 为中点,为正四棱柱表面上一点,且 , 则点的轨迹的长为( )A、 B、 C、 D、
10. 已知函数在处取得最大值,则( )A、 B、 C、 D、11. 设点 , , 圆: , 点满足 , 设点的轨迹为 , 与交于点 , , 为直线上一点(为坐标原点),则( )A、4 B、 C、2 D、12. 在正四棱柱中, , , 为中点,为正四棱柱表面上一点,且 , 则点的轨迹的长为( )A、 B、 C、 D、二、填空题
-
13. 函数在处的切线与直线平行,则a= .14. 设满足约束条件 , 则的最小值为 .15. 设双曲线 : 的右焦点为 ,直线 为双曲线 的一条渐近线,点 关于直线 的对称点为 ,若点 在双曲线 的左支上,则双曲线 的离心率为 .16. 已知函数 , 若函数 , 数列为等差数列, , 则 .
三、解答题
-
17. 在△ABC中,内角A、B、C的对边分别为a、b、c,且 .(1)、求角A的大小;(2)、若 , △ABC的面积为 , 求的值.18. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形, , , M,N分别是线段AB,PC的中点.
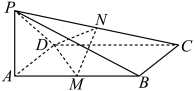 (1)、求证:MN平面PAD;(2)、在线段CD上是否存在一点Q,使得直线NQ与平面DMN所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.19. 强基计划校考由试点高校自主命题,校考过程中通过笔试后才能进入面试环节.已知甲、乙两所大学的笔试环节都设有三门考试科目且每门科目是否通过相互独立,若某考生报考甲大学,每门科目通过的概率均为;该考生报考乙大学,每门科目通过的概率依次为 , , m,其中 .(1)、若 , 分别求出该考生报考甲、乙两所大学在笔试环节恰好通过一门科目的概率;(2)、强基计划规定每名考生只能报考一所试点高校,若以笔试过程中通过科目数的数学期望为依据作决策,当该考生更希望通过乙大学的笔试时,求m的取值范围.20. 已知抛物线的焦点为 , 准线为 , 点为上的一点,过点作直线的垂线,垂足为 , 且 , .(1)、求抛物线的标准方程;(2)、已知的三个顶点都在抛物线上,顶点 , 重心恰好是抛物线的焦点 , 求所在的直线方程.
(1)、求证:MN平面PAD;(2)、在线段CD上是否存在一点Q,使得直线NQ与平面DMN所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.19. 强基计划校考由试点高校自主命题,校考过程中通过笔试后才能进入面试环节.已知甲、乙两所大学的笔试环节都设有三门考试科目且每门科目是否通过相互独立,若某考生报考甲大学,每门科目通过的概率均为;该考生报考乙大学,每门科目通过的概率依次为 , , m,其中 .(1)、若 , 分别求出该考生报考甲、乙两所大学在笔试环节恰好通过一门科目的概率;(2)、强基计划规定每名考生只能报考一所试点高校,若以笔试过程中通过科目数的数学期望为依据作决策,当该考生更希望通过乙大学的笔试时,求m的取值范围.20. 已知抛物线的焦点为 , 准线为 , 点为上的一点,过点作直线的垂线,垂足为 , 且 , .(1)、求抛物线的标准方程;(2)、已知的三个顶点都在抛物线上,顶点 , 重心恰好是抛物线的焦点 , 求所在的直线方程.