广西南宁市2023届高三理数二模试卷
试卷更新日期:2023-05-04 类型:高考模拟
一、单选题
-
1. 已知复数 , 则z的虚部为( )A、 B、 C、2 D、2. 已知集合 , , 则( )A、 B、 C、 D、3. 某商场一年中各月份的收入、支出情况的统计如图所示,则下列说法中不正确的是( )
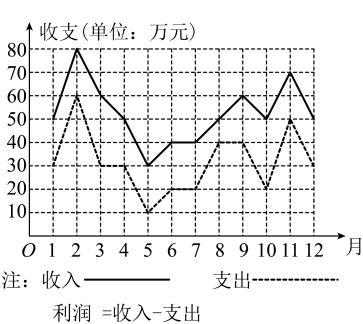 A、支出最高值与支出最低值的比是6:1 B、利润最高的月份是2月份 C、第三季度平均收入为50万元 D、1~2月份的支出的变化率与10~11月份的支出的变化率相同4. 已知 , 且 , 则( )A、 B、 C、 D、5. 一个几何体的正视图如图所示,则该几何体的俯视图不可能是( )
A、支出最高值与支出最低值的比是6:1 B、利润最高的月份是2月份 C、第三季度平均收入为50万元 D、1~2月份的支出的变化率与10~11月份的支出的变化率相同4. 已知 , 且 , 则( )A、 B、 C、 D、5. 一个几何体的正视图如图所示,则该几何体的俯视图不可能是( )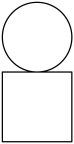 A、
A、 B、
B、 C、
C、 D、
D、 6. 函数的图象大致是( )A、
6. 函数的图象大致是( )A、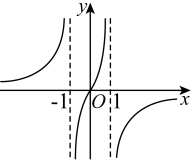 B、
B、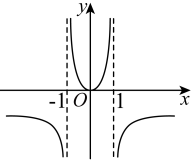 C、
C、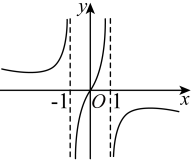 D、.
D、.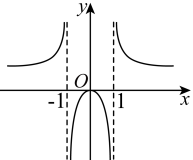 7. 现从3个男生2个女生共5人中任意选出3人参加某校高三年级的百日誓师大会,若选出的3人中,在有1人是女生的条件下,另2人是男生的概率为( )A、 B、 C、 D、8. 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为 m(如图所示),则旗杆的高度为( )
7. 现从3个男生2个女生共5人中任意选出3人参加某校高三年级的百日誓师大会,若选出的3人中,在有1人是女生的条件下,另2人是男生的概率为( )A、 B、 C、 D、8. 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为 m(如图所示),则旗杆的高度为( )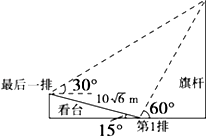 A、10m B、30m C、10m D、10m9. 已知椭圆与双曲线有共同的焦点 , , 离心率分别为 , , 点为椭圆与双曲线在第一象限的公共点,且 , 若 , 则椭圆的方程为( )A、 B、 C、 D、10. 已知函数的极值点为1,且 , 则的极小值为( )A、-1 B、 C、b D、411. 如图,在矩形中的曲线分别是 , 的一部分, , , 在矩形内随机取一点,若此点取自阴影部分的概率为 , 取自非阴影部分的概率为 , 则( )
A、10m B、30m C、10m D、10m9. 已知椭圆与双曲线有共同的焦点 , , 离心率分别为 , , 点为椭圆与双曲线在第一象限的公共点,且 , 若 , 则椭圆的方程为( )A、 B、 C、 D、10. 已知函数的极值点为1,且 , 则的极小值为( )A、-1 B、 C、b D、411. 如图,在矩形中的曲线分别是 , 的一部分, , , 在矩形内随机取一点,若此点取自阴影部分的概率为 , 取自非阴影部分的概率为 , 则( )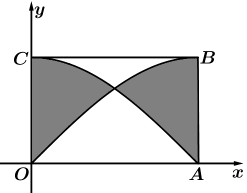 A、 B、 C、 D、大小关系不能确定12. 设 , , , 则( )A、 B、 C、 D、
A、 B、 C、 D、大小关系不能确定12. 设 , , , 则( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , , 且满足 , 则.14. 已知圆和直线 , 则与直线l平行且与圆C相切的直线方程为.15. 蹴鞠,又名“蹴球”“蹴圈”等,“蹴”有用脚蹴、踢的含义,鞠最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的足球,现已知某“鞠”的表面上有四个点满足 , , 则该“鞠”的表面积为.16. 已知当时,有 , 若对任意的都有 , 则.
三、解答题
-
17. 记为各项均为正数的等比数列的前n项和,且成等差数列.(1)、求的通项公式;(2)、设 , 求的前n项和.18. 如图,在四棱锥中,是边长为1的正三角形,面面 , , , , C为的中点.
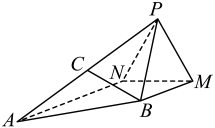 (1)、求证:平面;(2)、线段上是否存在点F,使二面角的余弦值为 , 若存在,求.若不存在,请说明理由.19. 随着科技的不断发展,“智能手机”已成为人们生活中不可缺少的必需品,下表是年广西某地市手机总体出货量(单位:万部)统计表.
(1)、求证:平面;(2)、线段上是否存在点F,使二面角的余弦值为 , 若存在,求.若不存在,请说明理由.19. 随着科技的不断发展,“智能手机”已成为人们生活中不可缺少的必需品,下表是年广西某地市手机总体出货量(单位:万部)统计表.年份
2018年
2019年
2020年
2021年
2022年
年份代码x
1
2
3
4
5
手机总体出货量y/万部
4.9
4.1
3.9
3.2
3.5
并计算求得
附:线性回归方程中斜率与截距的最小二乘估计公式分别为 , .
(1)、已知该市手机总体出货量y与年份代码x之间可用线性回归模型拟合,求y关于x的线性回归方程;(2)、预测2023年该市手机总体出货量.20. 已知抛物线经过点 , 过点的直线l与抛物线C有两个不同交点A,B,且直线交y轴于M,直线变y轴于N.(1)、求直线l斜率的取值范围;(2)、证明:存在定点T,使得 , 且.