广东省湛江市2023届高三数学二模试卷

试卷更新日期：2023-05-04 类型：高考模拟

进入出卷网下载

一、单选题

1. 设复数 $z$ 在复平面内对应的点为 $(2 ， 5)$ ，则 $1 + \bar{z}$ 在复平面内对应的点为（）

A、 $(3 ， - 5)$ B、 $(3 ， 5)$ C、 $(- 3 ， - 5)$ D、 $(- 3 ， 5)$

查看试题解析
2. 已知集合 $A = {x | x^{2} - 3 x > 4}$ ， $B = {x | 2^{x} > 2}$ ，则 $(∁_{R} A) ∩ B =$ （）

A、 $[- 1 ， 2)$ B、 $(4 ， + \infty)$ C、 $(1 ， 4)$ D、 $(1 ， 4]$

查看试题解析

3. 广东省第七次人口普查统计数据显示，湛江市九个管辖区常住人口数据如表所示，则这九个管辖区的数据的第70%分位数是（）

管辖区	常住人口
赤坎区	303824
霞山区	487093
坡头区	333239
麻章区	487712
遂溪县	886452
徐闻县	698474
廉江市	1443099
雷州市	1427664
吴川市	927275

A、927275 B、886452 C、698474 D、487712

查看试题解析

4. ${(2 x^{2} - \frac{1}{x})}^{5}$ 的展开式中， $x^{4}$ 的系数是（）

A、40 B、-40 C、80 D、-80

查看试题解析
5. 如图，将一个圆柱 $2 n (n \in N^{*})$ 等分切割，再将其重新组合成一个与圆柱等底等高的几何体， $n$ 越大，重新组合成的几何体就越接近一个“长方体”．若新几何体的表面积比原圆柱的表面积增加了10，则圆柱的侧面积为（）

A、 $10 π$ B、 $20 π$ C、 $10 n π$ D、 $18 π$

查看试题解析
6. 若与 $y$ 轴相切的圆 $C$ 与直线 $l ： y = \frac{\sqrt{3}}{3} x$ 也相切，且圆 $C$ 经过点 $P (2 ， \sqrt{3})$ ，则圆 $C$ 的直径为（）

A、2 B、2或 $\frac{14}{3}$ C、 $\frac{7}{4}$ D、 $\frac{7}{4}$ 或 $\frac{16}{3}$

查看试题解析
7. 当 $x$ ， $y \in (0 ， + \infty)$ 时， $\frac{4 x^{4} + 17 x^{2} y + 4 y^{2}}{x^{4} + 2 x^{2} y + y^{2}} < \frac{m}{4}$ 恒成立，则m的取值范围是（）

A、 $(25 ， + \infty)$ B、 $(26 ， + \infty)$ C、 $(\frac{99}{4} ， + \infty)$ D、 $(27 ， + \infty)$

查看试题解析
8. 对于两个函数 $h (t) = e^{t - 1} (t > \frac{1}{2})$ 与 $g (t) = l n (2 t - 1) + 2 (t > \frac{1}{2})$ ，若这两个函数值相等时对应的自变量分别为 $t_{1}$ ， $t_{2}$ ，则 $t_{2} - t_{1}$ 的最小值为（）

A、-1 B、 $- l n 2$ C、 $1 - l n 3$ D、 $1 - 2 l n 2$

查看试题解析

二、多选题

9. 若 $5 s i n 2 α + 5 c o s 2 α + 1 = 0$ ，则 $t a n α$ 的值可能为（）

A、2 B、3 C、 $- \frac{1}{3}$ D、 $- \frac{1}{2}$

查看试题解析
10. 一百零八塔始建于西夏时期，是中国现存最大且排列最整齐的塔群之一，塔群随山势凿石分阶而建，自上而下一共12层，第1层有1座塔，从第2层开始每层的塔数均不少于上一层的塔数，总计108座塔．已知包括第1层在内的其中10层的塔数可以构成等差数列 ${a_{n}}$ ，剩下的2层的塔数分别与上一层的塔数相等，第1层与第2层的塔数不同，则（）

A、第3层的塔数为3 B、第6层的塔数为9 C、第4层与第5层的塔数相等 D、等差数列 ${a_{n}}$ 的公差为2

查看试题解析
11. 廉江红橙是广东省廉江市特产、中国国家地理标志产品．设廉江地区某种植园成熟的红橙单果质量 $M$ （单位：g）服从正态分布 $N (165 ， σ^{2})$ ，且 $P (M < 162) = 0.15$ ， $P (165 < M < 167) = 0.3$ ．下列说法正确的是（）

A、若从种植园成熟的红橙中随机选取1个，则这个红橙的质量小于167 g的概率为0.7 B、若从种植园成熟的红橙中随机选取1个，则这个红橙的质量在167 g～168 g的概率为0.05 C、若从种植园成熟的红橙中随机选取600个，则质量大于163 g的个数的数学期望为480 D、若从种植园成熟的红橙中随机选取600个，则质量在163 g～168 g的个数的方差为136.5

查看试题解析
12. 已知双曲线 $C ： \frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的上焦点为 $F$ ，过焦点 $F$ 作 $C$ 的一条渐近线的垂线，垂足为 $A$ ，并与另一条渐近线交于点 $B$ ，若 $| F B | = 4 | A F |$ ，则 $C$ 的离心率可能为（）

A、 $\frac{2 \sqrt{6}}{3}$ B、 $\frac{\sqrt{15}}{3}$ C、 $\frac{2 \sqrt{10}}{5}$ D、 $\frac{2 \sqrt{5}}{3}$

查看试题解析

三、填空题

13. 已知奇函数 $f (x) = {\begin{array}{l} x^{2} - 3^{- x} ， x < 0 ， \\ g (x) + 1 ， x > 0 ， \end{array}$ 则 $g (x) =$ ．

查看试题解析
14. 若抛物线 $C$ 的焦点到准线的距离为 $\sqrt{3}$ ，且 $C$ 的开口朝上，则 $C$ 的标准方程为．

查看试题解析
15. 若函数 $f (x) = s i n (ω x + \frac{π}{3}) (ω > 0)$ 在 $(- \frac{π}{6} ， \frac{π}{18})$ 上具有单调性，且 $x = \frac{2 π}{9}$ 为 $f (x)$ 的一个零点，则 $f (x)$ 在 $(- \frac{π}{6} ， \frac{π}{18})$ 上单调递（填增或减），函数 $y = f (x) - l g x$ 的零点个数为．

查看试题解析
16. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形， $A P ⊥$ 底面 $A B C D$ ， $E$ 为棱 $A B$ 上任意一点（不包括端点）， $F$ 为棱 $P D$ 上任意一点（不包括端点），且 $\frac{A E}{A B} = \frac{D F}{D P}$ ．已知 $A B = A P = 1$ ， $B C = 2$ ，当三棱锥 $C - B E F$ 的体积取得最大值时， $E F$ 与底面 $A B C D$ 所成角的正切值为．

查看试题解析

四、解答题

17. 现有A，B两个广西旅行社，统计了这两个旅行社的游客去漓江、乐满地主题乐园、西街、龙脊梯田四个景点旅游的各240人次的数据，并分别绘制出这两个旅行社240人次分布的柱形图，如图所示．假设去漓江、乐满地主题乐园、西街、龙脊梯田旅游每人次的平均消费分别为1200元、1000元、600元、200元．

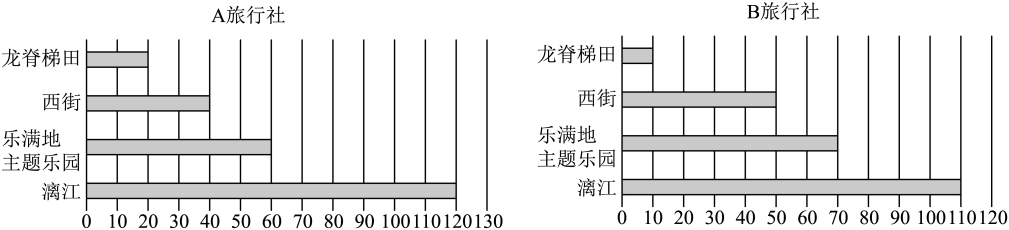(1)、通过计算，比较这两个旅行社240人次的消费总额哪个更大；

(2)、若甲和乙分别去A旅行社、B旅行社，并都从这四个景点中选择一个去旅游，以这240人次去漓江的频率为概率，求甲、乙至少有一人去漓江的概率．

查看试题解析
18. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $b^{2} + c^{2} = a^{2} - b c$ ．

(1)、求 $A$ ；

(2)、若 $b s i n A = 4 s i n B$ ，且 $l g b + l g c \geq 1 - 2 c o s (B + C)$ ，求 $△ A B C$ 面积的取值范围．

查看试题解析
19. 如图1，在五边形 $A B C D E$ 中，四边形 $A B C E$ 为正方形， $C D ⊥ D E$ ， $C D = D E$ ，如图2，将 $△ A B E$ 沿 $B E$ 折起，使得 $A$ 至 $A_{1}$ 处，且 $A_{1} B ⊥ D E$ ．

(1)、证明： $D E ⊥$ 平面 $A_{1} B E$ ．

(2)、求二面角 $C - A_{1} E - D$ 的余弦值．

查看试题解析
20. 已知两个正项数列 ${a_{n}}$ ， ${b_{n}}$ 满足 $\frac{1}{a_{n} - b_{n}} = b_{n}$ ， $\frac{1}{a_{n}} = \frac{b_{n}}{n^{2} + 1}$ ．

(1)、求 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、用 $[x]$ 表示不超过 $x$ 的最大整数，求数列 ${[a_{n} + a_{n + 1}] \cdot 2^{b_{n}}}$ 的前 $n$ 项和 $S_{n}$ ．

查看试题解析
21. 设椭圆方程为 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ， $A (- 2 ， 0)$ ， $B (2 ， 0)$ 分别是椭圆的左、右顶点，直线 $l$ 过点 $C (6 ， 0)$ ，当直线 $l$ 经过点 $D (- 2 ， \sqrt{2})$ 时，直线 $l$ 与椭圆相切．

(1)、求椭圆的方程．

(2)、若直线 $l$ 与椭圆交于 $P$ ， $Q$ （异于 $A$ ， $B$ ）两点．
（i）求直线 $B P$ 与 $B Q$ 的斜率之积；
（ii）若直线 $A P$ 与 $B Q$ 的斜率之和为 $- \frac{1}{2}$ ，求直线 $l$ 的方程．

查看试题解析
22. 已知函数 $f (x) = e^{x - 1} - \frac{1}{2} x^{2} + x - m l n x$ ．

(1)、求曲线 $y = f (x)$ 在 $x = 1$ 处的切线方程．

(2)、若存在 $x_{1} \neq x_{2}$ 使得 $f (x_{1}) = f (x_{2})$ ，证明：
（i） $m > 0$ ；
（ii） $2 m > e (l n x_{1} + l n x_{2})$ ．

查看试题解析