广东省深圳市2023届高三数学二模试卷

试卷更新日期：2023-05-04 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {2 ， 0}$ ， $B = {2 ， 3}$ ，则 $∁_{A \cup B} (A \cap B) =$ （）

A、{0} B、{2} C、{3} D、{0，3}

查看试题解析
2. 已知函数 $f (x) = {\begin{array}{l} 3^{x} ， x \leq 1 \\ l o g_{3} x ， x > 1 \end{array}$ ，则 $f (f (2)) =$ （）

A、2 B、-2 C、 $\frac{1}{2}$ D、- $\frac{1}{2}$

查看试题解析
3. 设等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，若 $S_{10} = 20$ ， $S_{20} = 10$ ，则 $S_{30} =$ （）

A、0 B、-10 C、-30 D、-40

查看试题解析
4. 设表面积相等的正方体、正四面体和球的体积分别为 $V_{1}$ 、 $V_{2}$ 和 $V_{3}$ ，则（）

A、 $V_{1} < V_{2} < V_{3}$ B、 $V_{2} < V_{1} < V_{3}$ C、 $V_{3} < V_{1} < V_{2}$ D、 $V_{3} < V_{2} < V_{1}$

查看试题解析
5. 已知 $△ O A B$ 中， $\vec{O C} = \vec{C A}$ ， $\vec{O D} = 2 \vec{D B}$ ， $A D$ 与 $B C$ 相交于点 $M$ ， $\vec{O M} = x \vec{O A} + y \vec{O B}$ ，则有序数对 $(x ， y) =$ （）

A、 $(\frac{1}{2} ， \frac{1}{3})$ B、 $(\frac{1}{3} ， \frac{1}{2})$ C、 $(\frac{1}{2} ， \frac{1}{4})$ D、 $(\frac{1}{4} ， \frac{1}{2})$

查看试题解析
6. 从1，2，3，4，5中随机选取三个不同的数，若这三个数之积为偶数，则它们之和大于8的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析
7. 设椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，直线l过点 $F_{1}$ .若点 $F_{2}$ 关于l的对称点P恰好在椭圆C上，且 $\vec{F_{1} P} \cdot \vec{F_{1} F_{2}} = \frac{1}{2} a^{2}$ ，则C的离心率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{5}$

查看试题解析
8. 已知 $ε > 0$ ， $x ， y \in (- \frac{π}{4} ， \frac{π}{4})$ ，且 $e^{x + ε} s i n y = e^{y} s i n x$ ，则下列关系式恒成立的为（）

A、 $c o s x \leq c o s y$ B、 $c o s x \geq c o s y$ C、 $s i n x \leq s i n y$ D、 $s i n x \geq s i n y$

查看试题解析

二、多选题

9. 为了研究y关于x的线性相关关系，收集了5组样本数据(见下表)：
x
1
2
3
4
5
y
0.5
0.8
1
1.2
1.5
假设经验回归方程为 $\hat{y} = \hat{b} x + 0.28$ ，则（）

A、 $\hat{b} = 0.24$ B、当 $x = 8$ 时，y的预测值为2.2 C、样本数据y的40%分位数为0.8 D、去掉样本点 $(3 ， 1)$ 后，x与y的样本相关系数r不变

查看试题解析
10. 已知 $f (x)$ 是定义在闭区间上的偶函数，且在y轴右侧的图象是函数 $y = s i n (ω x + ϕ)$ $(ω > 0 ， 0 < φ < π)$ 图象的一部分(如图所示)，则（）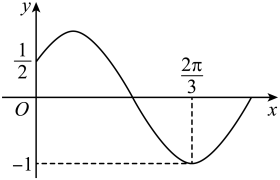

A、 $f (x)$ 的定义域为 $[- π ， π]$ B、当 $x = \frac{π}{6}$ 时， $f (x)$ 取得最大值 C、当 $x < 0$ 时， $f (x)$ 的单调递增区间为 $[- \frac{2 π}{3} ， - \frac{π}{6}]$ D、当 $x < 0$ 时， $f (x)$ 有且只有两个零点 $- \frac{5 π}{12}$ 和 $- \frac{11 π}{12}$

查看试题解析
11. 如图，在矩形AEFC中， $A E = 2 \sqrt{3}$ ， EF=4，B为EF中点，现分别沿AB、BC将△ABE、△BCF翻折，使点E、F重合，记为点P，翻折后得到三棱锥P-ABC，则（）

A、三棱锥 $P - A B C$ 的体积为 $\frac{4 \sqrt{2}}{3}$ B、直线PA与直线BC所成角的余弦值为 $\frac{\sqrt{3}}{6}$ C、直线PA与平面PBC所成角的正弦值为 $\frac{1}{3}$ D、三棱锥 $P - A B C$ 外接球的半径为 $\frac{\sqrt{22}}{2}$

查看试题解析
12. 设抛物线C： $y = x^{2}$ 的焦点为F，过抛物线C上不同的两点A，B分别作C的切线，两条切线的交点为P，AB的中点为Q，则（）

A、 $P Q ⊥ x$ 轴 B、 $P F ⊥ A B$ C、 $∠ P F A = ∠ P F B$ D、 $| A F | + | B F | = 2 | P F |$

查看试题解析

三、填空题

13. 已知复数 $z$ 满足 $z^{2} + z + 1 = 0$ ，则 $z \cdot \bar{z} =$ .

查看试题解析
14. 若 $X ∼ N (9 ， 2^{2})$ ，则 $P (7 < X < 13) =$ (精确到0.01).
参考数据：若 $X \sim N (μ ， σ^{2})$ ，则 $(| x - μ | < σ) \approx 0.683$ ， $P (| X - μ | < 2 σ) \approx 0.955$ .

查看试题解析
15. 已知函数 $f (x)$ 的定义域为 $R$ ，若 $f (x + 1) - 2$ 为奇函数，且 $f (1 - x) = f (3 + x)$ ，则 $f (2023) =$ .

查看试题解析
16. 足球是一项很受欢迎的体育运动.如图，某标准足球场的 $B$ 底线宽 $A B = 72$ 码，球门宽 $E F = 8$ 码，球门位于底线的正中位置.在比赛过程中，攻方球员带球运动时，往往需要找到一点 $P$ ，使得 $∠ E P F$ 最大，这时候点 $P$ 就是最佳射门位置.当攻方球员甲位于边线上的点 $O$ 处（ $O A = A B$ ， $O A ⊥ A B$ ）时，根据场上形势判断，有 $\vec{O A}$ 、 $\vec{O B}$ 两条进攻线路可供选择.若选择线路 $\vec{O A}$ ，则甲带球码时， $A P O$ 到达最佳射门位置；若选择线路 $\vec{O B}$ ，则甲带球码时，到达最佳射门位置.

查看试题解析

四、解答题

17. 已知 $a ， b ， c$ 分别为 $△ A B C$ 三个内角 $A ， B ， C$ 的对边，且 $s i n (A - B) = 2 s i n C$ .

(1)、证明： $a^{2} = b^{2} + 2 c^{2}$ ；

(2)、若 $A = \frac{2 π}{3}$ ， $a = 3$ ， $\vec{B C} = 3 \vec{B M}$ ，求AM的长度.

查看试题解析
18. 飞盘运动是一项入门简单，又具有极强的趣味性和社交性的体育运动，目前已经成为了年轻人运动的新潮流.某俱乐部为了解年轻人爱好飞盘运动是否与性别有关，对该地区的年轻人进行了简单随机抽样，得到如下列联表：
性别
飞盘运动
合计
不爱好
爱好
男
6
16
22
女
4
24
28
合计
10
40
50
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$α$
0.1
0.01
0.001
$x_{α}$
2.706
6.635
10.828

(1)、在上述爱好飞盘运动的年轻人中按照性别采用分层抽样的方法抽取10人，再从这10人中随机选取3人访谈，记参与访谈的男性人数为X，求X的分布列和数学期望；

(2)、依据小概率值 $α = 0.01$ 的独立性检验，能否认为爱好飞盘运动与性别有关联？如果把上表中所有数据都扩大到原来的10倍，在相同的检验标准下，再用独立性检验推断爱好飞盘运动与性别之间的关联性，结论还一样吗？请解释其中的原因.

查看试题解析
19. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = B C = 2$ ， $∠ A B C = \frac{2 π}{3}$ ， $A_{1} C_{1} ⊥ A_{1} B$ .

(1)、证明： $A_{1} A = A_{1} C$ ；

(2)、若 $A_{1} A = 2$ ， $B C_{1} = \sqrt{14}$ ，求平面 $A_{1} C B_{1}$ 与平面 $B C C_{1} B_{1}$ 夹角的余弦值.

查看试题解析
20. 已知数列 ${a_{n}}$ 满足， $a_{1} = 3$ ， $a_{n} a_{n + 1} = 9 \times 2^{2 n - 1}$ ， $n \in N^{*}$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、证明：数列 ${a_{n}}$ 中的任意三项均不能构成等差数列.

查看试题解析
21. 已知双曲线： $x^{2} - y^{2} = 1$ ，点M为双曲线C右支上一点，A、B为双曲线C的左、右顶点，直线 $A M$ 与y轴交于点D，点Q在x轴正半轴上，点E在y轴上.

(1)、若点 $M (2 ， \sqrt{3})$ ， $Q (2 ， 0)$ ，过点Q作BM的垂线l交该双曲线C于S，T两点，求 $△ O S T$ 的面积；

(2)、若点M不与B重合，从下面①②③中选取两个作为条件，证明另外一个成立.① $\vec{O D} = \vec{D E}$ ；② $B M ⊥ E Q$ ；③ $| O Q | = 2$ .注：若选择不同的组合分别解答，则按第一个解答计分.

查看试题解析
22. 已知函数 $f (x) = e^{m x - 1} - x$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、当 $m > 0$ 时，函数 $g (x) = f (x) - \frac{l n x + 1}{m} + x$ 恰有两个零点.
（i）求m的取值范围；
（ii）证明： $g (x) > m^{\frac{1}{m}} - m^{- \frac{1}{m}}$ .

查看试题解析

性别	飞盘运动		合计
性别	不爱好	爱好	合计
男	6	16	22
女	4	24	28
合计	10	40	50

x	1	2	3	4	5
y	0.5	0.8	1	1.2	1.5

$α$	0.1	0.01	0.001
$x_{α}$	2.706	6.635	10.828