安徽省淮南市2023届高三数学二模试卷

试卷更新日期：2023-05-04 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $A = {x \in R | y = \sqrt{1 + x}}$ ，则 $∁_{U} A =$ （）

A、 ${x | x < - 1}$ B、 ${x | x < 0}$ C、 ${x | x \leq - 1}$ D、 ${x | x \geq - 1}$

查看试题解析
2. 已知复数z满足 $(2 - i) \cdot z = i^{2023}$ ，（i是虚数单位），则复数z在复平面内所对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 四位同学各自在“五一”劳动节五天假期中任选一天参加公益活动，则甲在5月1日、乙不在5月1日参加公益活动的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{4}{5}$ C、 $\frac{1}{25}$ D、 $\frac{4}{25}$

查看试题解析
4. 已知函数 $f (x) = A s i n (ω x + φ)$ ，（ $A > 0$ ， $ω > 0$ ， $| ϕ | < \frac{π}{2}$ ）的相邻两个对称中心距离为 $\frac{π}{2}$ 且图象经过 $M (\frac{π}{6} ， A)$ ，若将 $f (x)$ 图象上的所有点向右平移 $\frac{π}{6}$ 个单位长度得到函数 $g (x)$ 的图象，则函数 $g (x)$ 的单调递减区间是（）

A、 $[k π - \frac{π}{6} ， k π + \frac{π}{3}]$ ， $k ∈ Z$ B、 $[k π + \frac{π}{3} ， k π + \frac{5 π}{6}]$ ， $k ∈ Z$ C、 $[k π ， k π + \frac{π}{2}]$ ， $k ∈ Z$ D、 $[k π + \frac{π}{4} ， k π + \frac{3}{4} π]$ ， $k ∈ Z$

查看试题解析
5. 在△ABC中，已知 $∠ A C B = \frac{2 π}{3}$ ， $B C = 4$ ， $A C = 3$ ， D是边AB的中点，点E满足 $\vec{A E} = \frac{3}{4} \vec{A B} + \frac{1}{4} \vec{A C}$ ，则 $\vec{C D} \cdot \vec{D E} =$ （）

A、 $- \frac{5}{8}$ B、－1 C、 $\frac{1}{2}$ D、 $\frac{1}{8}$

查看试题解析
6. 我国古代数学在宋元时期达到繁荣的顶点，涌现了一大批卓有成就的数学家，其中朱世杰与秦九韶、杨辉、李冶被誉为我国“宋元数学四大家”.朱世杰著有《四元玉鉴》和《算学启蒙》等，在《算学启蒙》中，最为引人入胜的问题莫过于堆垛问题，其中记载有以下问题：“今有三角、四角果子垛各一所，共积六百八十五个，只云三角底子一面不及四角底子一面七个，问二垛底子一面几何？”其中“积”是和的意思，“三角果子垛”是每层都是正三角形的果子垛，自上至下依次有1，3，6，10，15，…，个果子，“四角果子垛”是每层都是正方形的果子垛，自上至下依次有1，4，9，16，…，个果子，“底子一面”指每垛最底层每条边”.根据题意，可知该三角、四角果子垛最底层每条边上的果子数是（）（参考公式： $1^{2} + 2^{2} + 3^{2} + ⋯ + n^{2} = \frac{n (n + 1) (2 n + 1)}{6}$ ）

A、4，11 B、5，12 C、6，13 D、7，14

查看试题解析
7. 如图， $α ⊥ β$ ， $α ∩ β = l$ ， $A \in α$ ， $B \in β$ ，点 $A ， B$ 在棱 $l$ 上的射影分别是 $A_{1} ， B_{1}$ ，若 $A A_{1} = B B_{1} = 2$ ， $A B = 4$ ，则异面直线 $A B_{1}$ 与 $A_{1} B$ 所成角的余弦值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
8. 定义在 $R$ 上的函数 $f (x)$ 满足 $f (- x) + f (x) + 2 c o s x = 0$ ，当 $x \geq 0$ 时， $f^{'} (x) > s i n x$ ，则不等式 $f (x) + 2$ $c o s x > f (π - x)$ 的解集为（）

A、 $(\frac{π}{2} ， + \infty)$ B、 $(- \infty ， \frac{π}{2})$ C、 $(- \frac{π}{2} ， \frac{π}{2})$ D、 $(- \infty ， π)$

查看试题解析

二、多选题

9. 已知单位向量 $\vec{a}$ ， $\vec{b}$ ，则下列命题正确的是（）

A、向量 $\vec{a}$ ， $\vec{b}$ 不共线，则 $(\vec{a} + \vec{b}) ⊥ (\vec{a} - \vec{b})$ B、若 $\vec{a} = (- \frac{\sqrt{3}}{2} ， t)$ ， $\vec{b} = (c o s α ， s i n α)$ ，且 $\vec{a} / / \vec{b}$ ，则 $t a n α = \frac{\sqrt{3}}{3}$ C、若 $| \vec{a} - \vec{b} | ≥ \sqrt{3}$ ，记向量 $\vec{a}$ ， $\vec{b}$ 的夹角为θ，则θ的最小值为 $\frac{2 π}{3}$ . D、若 $〈 \vec{a} ， \vec{b} 〉 = \frac{2 π}{3}$ ，则向量 $\vec{b}$ 在向量 $\vec{a}$ 上的投影向量是 $\frac{1}{2} \vec{a}$

查看试题解析
10. 已知圆M的方程为： $x^{2} + y^{2} + a x + a y - 2 a - 4 = 0$ ，（ $a \in R$ ），点 $P (1 ， 1)$ ，给出以下结论，其中正确的有（）

A、过点P的任意直线与圆M都相交 B、若圆M与直线 $x + y + 2 = 0$ 无交点，则 $a \in (- \frac{1}{2} ， + \infty)$ C、圆M面积最小时的圆与圆Q： $x^{2} + y^{2} + 6 x - 10 y + 16 = 0$ 有三条公切线 D、无论a为何值，圆M都有弦长为 $2 \sqrt{2}$ 的弦，且被点P平分

查看试题解析
11. 如图，棱长为2的正四面体 $A B C D$ 中， $M ， N$ 分别为棱 $A D ， B C$ 的中点，O为线段 $M N$ 的中点，球O的表面正好经过点M，则下列结论中正确的是（）

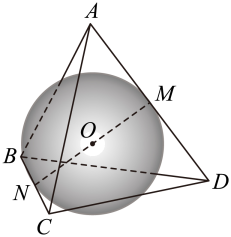A、 $A O ⊥$ 平面 $B C D$ B、球O的体积为 $\frac{\sqrt{2}}{3} π$ C、球O被平面 $B C D$ 截得的截面面积为 $\frac{4}{3} π$ D、球O被正四面体 $A B C D$ 表面截得的截面周长为 $\frac{8 \sqrt{3}}{3} π$

查看试题解析
12. 当一个圆沿着一条定直线无滑动地滚动时，圆周上一个定点的轨迹称为摆线.如图，圆心为 $B (0 ， 1)$ ，半径为1的圆B，圆上定点M初始位置在原点，当圆B沿着x轴正向滚动，且半径BM旋转角度为φ，则以下结论正确的为（）

A、若 $φ = \frac{π}{3}$ ，则点M的坐标为 $(\frac{2 π - 3 \sqrt{3}}{6} ， \frac{1}{2})$ B、圆B滚动一周，得到的摆线长等于圆周长 C、若圆B滚动角度 $π$ 时，点M从一个位置P到达位置Q，则PQ长度的最大值为 $π + 2$ D、若定点M总在直线 $x - y + a = 0$ 的下方，则a的取值范围为 $a > 2 - \frac{π}{2}$

查看试题解析

三、填空题

13. 已知二项式 ${(1 + x + \frac{a}{x^{2}})}^{5}$ 的常数项为 $- 59$ ，则 $a =$ .

查看试题解析
14. 近年来，我国肥胖人群的规模急速增长，肥胖人群有很大的心血管安全隐患.目前，国际上常用身体质量指数（BMI）来衡量人体胖瘦程度以及是否健康，其计算公式是 $B M I = \frac{体重 (单位：千克)}{身高^{2} (单位：米)}$ .我国成人的BMI数值标准为： $B M I < 18.5$ 为偏瘦， $18.5 \leq B M I < 24$ 为正常， $24 \leq B M I < 28$ 为偏胖， $B M I \geq 28$ 为肥胖.为了解某公司员工的身体肥胖情况，研究人员从公司员工体检数据中，利用分层抽样得到15名员工的BMI数据如下：23.5，21.6，30.6，22.1，23.7，20.6，25.5，23.9，20.8，21.5，21.8，18.2，25.2，21.5，19.1.则该组数据的第70百分位数为.

查看试题解析
15. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前n项和.已知 $\frac{3 S_{n}}{n} + n = 3 a_{n} + 1$ ， $a_{1} = - \frac{1}{3}$ ，则数列 ${a_{n}}$ 的通项公式，是.

查看试题解析
16. 双曲线 $C ： x^{2} - \frac{y^{2}}{t} = 1 (t > 0)$ 的离心率为 $\sqrt{3}$ ， $A ， B$ 分别是 $C$ 的左，右顶点， $P$ 是 $C$ 上异于 $A ， B$ 的一动点，直线 $P A ， P B$ 分别与 $y$ 轴交于点 $M ， N$ ，请写出所有满足条件 $\vec{Q M} \cdot \vec{Q N} = 0$ 的定点 $Q$ 的坐标.

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 满足 $a_{n + 1} - a_{n} = 2^{n}$ ，且 $a_{1} = 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{a_{n} + 1}{a_{n} a_{n + 1}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 已知 $f (x) = 2 c o s x \cdot s i n (x + \frac{π}{6})$ ， $x ∈ R$ ， $△ A B C$ 的内角A，B，C所对的，边分别为a，b，c，若 $f (x)$ 的最大值为 $f (A)$ .

(1)、求A；

(2)、当 $a = 2$ ， $b = 2 \sqrt{3}$ 时，求 $△ A B C$ 的面积.

查看试题解析
19. 2022年10月16日至10月22日，中国共产党第二十次全国代表大会在北京召开，此次大会是在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的一次十分重要的大会.在树人中学团委的组织下，高二年级各班团支部举行了“学习二十大，做有为青年”的知识竞赛活动，经过激烈竞争，高二（1）班（以下简称一班）和高二（3）班（以下简称三班）进入了最后的年级决赛，决赛规定：共进行5轮比赛，每轮比赛每个班可以从A，B两个题库中任选1题作答，在前两轮比赛中每个班的题目必须来自同一题库，后三轮比赛中每个班的题目必须来自同一题库，A题库每题20分，B题库每题30分，一班能正确回答A、B题库每题的概率分别为 $\frac{3}{4}$ 、 $\frac{1}{2}$ ，三班能正确回答A、B题库每题的概率均为 $\frac{2}{3}$ ，且每轮答题结果互不影响.

(1)、若一班前两轮选A题库，后三轮选B题库，求其总分不少于100分的概率；

(2)、若一班和三班在前两轮比赛中均选了B题库，而且一班两轮得分60分，三班两轮得分30分，一班后三轮换成A题库，三班后三轮不更换题库，设一班最后的总分为X，求X的分布列，并从每班总分的均值来判断，哪个班赢下这场比赛？

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，底面ABCD是梯形， $A B / / C D$ ， $B D = D C = 2 A B = 2$ ， $B D ⊥ C D$ ， $△ P B D$ 是等边三角形且与底面垂直，E是棱PA上一点， $\vec{A E} = λ \vec{E P}$ .

(1)、当 $P C / /$ 平面EBD，求实数λ的值；

(2)、当λ为何值时，平面EBD与平面PBD所成的锐二面角的大小为 $\frac{π}{6}$ ？

查看试题解析
21. 已知点 $F (1 ， 0)$ ，圆C： ${(x + 1)}^{2} + y^{2} = 9$ ，过点F的直线l交圆C于A，B两点，线段AB的中点为 $M (x_{0} ， y_{0})$ .

(1)、求动点 $P (2 x_{0} ， \sqrt{3} y_{0})$ 的轨迹Γ方程；

(2)、设轨迹Γ与x轴交于D，E两点（点E在点D的右侧），过点D作x轴的垂线m，过点F作直线DP的垂线n，垂线m与n交于点Q，求证：点P，Q，E共线.

查看试题解析
22. 已知函数 $f (x) = x e^{\frac{a}{x}} + l n x + \frac{a}{x}$ ， $x \in (0 ， + \infty)$ ，其中 $a \in R$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若方程 $f (x) = e + 1$ 恰有两个根，求a的取值范围.

查看试题解析