山东省东营市广饶县2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( ).A、 B、 C、 D、3. 如图,直线 , 将含角的直角三角板按图中位置摆放,若 , 则的度数为( )
2. 下列计算正确的是( ).A、 B、 C、 D、3. 如图,直线 , 将含角的直角三角板按图中位置摆放,若 , 则的度数为( )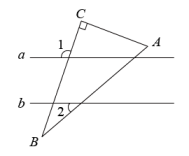 A、 B、 C、 D、4. 实数a,b在数轴上对应点的位置如图所示,下列结论正确的是( )
A、 B、 C、 D、4. 实数a,b在数轴上对应点的位置如图所示,下列结论正确的是( )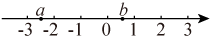 A、 B、 C、 D、5. 小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、6. 如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图描述正确的是( )
A、 B、 C、 D、5. 小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、6. 如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图描述正确的是( )
 A、俯视图不变,左视图不变 B、主视图改变,左视图改变 C、俯视图不变,主视图不变 D、主视图改变,俯视图改变7. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、8. 如图,抛物线和直线都经过点 , 抛物线的对称轴为 , 那么下列说法正确的是( )
A、俯视图不变,左视图不变 B、主视图改变,左视图改变 C、俯视图不变,主视图不变 D、主视图改变,俯视图改变7. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、8. 如图,抛物线和直线都经过点 , 抛物线的对称轴为 , 那么下列说法正确的是( ) A、 B、 C、 D、是不等式的解9. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为( )
A、 B、 C、 D、是不等式的解9. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为( ) A、 B、 C、 D、10. 如图,已知点A,B在反比例函数的图象上,点P沿C→A→B→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴于点M,设点P的运动时间为t,POM的面积为S,则S关于t的函数图象大致为( )
A、 B、 C、 D、10. 如图,已知点A,B在反比例函数的图象上,点P沿C→A→B→O的路线(图中“→”所示路线)匀速运动,过点P作PM⊥x轴于点M,设点P的运动时间为t,POM的面积为S,则S关于t的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
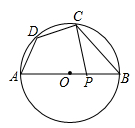
11. 冠状病毒因在显微镜下观察类似王冠而得名,新型冠状病毒的半径约是0.000000045米,将数0.000000045用科学记数法表示为 .12. 因式分解: .13. 甲、乙两名学生10次立定跳远成绩的平均数相同,若甲生10次立定跳远成绩的方差为 , 乙生10次立定跳远成绩的方差为 , 则甲、乙两名学生10次立定跳远成绩比较稳定的是 . (填“甲”或“乙”)14. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为 .
 15. 如图,一艘轮船位于灯塔P的南偏东 方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东 方向上的B处,此时B处与灯塔P的距离为海里(结果保留根号).
15. 如图,一艘轮船位于灯塔P的南偏东 方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东 方向上的B处,此时B处与灯塔P的距离为海里(结果保留根号).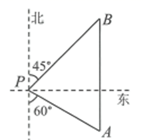 16. 如图,在平行四边形中, . 利用尺规在上分别截取 , 使;再分别以点为圆心,大于的长为半径作弧,两弧在内交于点G;作射线交于点H.若 , 则的长为 .
16. 如图,在平行四边形中, . 利用尺规在上分别截取 , 使;再分别以点为圆心,大于的长为半径作弧,两弧在内交于点G;作射线交于点H.若 , 则的长为 . 17. 关于x的函数的图象与x轴有两个交点,则k的取值范围是 .18. 如图,已知直线 : ,过点 作x轴的垂线交直线 于点 ,在线段 右侧作等边三角形 ,过点 作x轴的垂线交x轴于 ,交直线L于点 ,在线段 右侧作等边三角形 ,按此作法继续下去则 的纵坐标为 . (n为正整数)
17. 关于x的函数的图象与x轴有两个交点,则k的取值范围是 .18. 如图,已知直线 : ,过点 作x轴的垂线交直线 于点 ,在线段 右侧作等边三角形 ,过点 作x轴的垂线交x轴于 ,交直线L于点 ,在线段 右侧作等边三角形 ,按此作法继续下去则 的纵坐标为 . (n为正整数)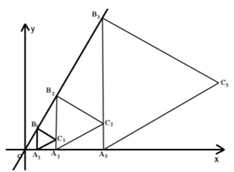
三、解答题
-
19.(1)、计算:;(2)、解不等式组: , 并写出它的所有整数解.20. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校以中国传统节日端午节为契机,组织全体学生参加包粽子劳动体验活动,随机调查了部分学生,对他们每个人平均包一个粽子的时长进行统计,并根据统计结果绘制成如下不完整的统计图表.
等级
时长:(单位:分钟)
人数
所占百分比
4
20
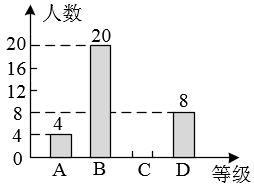
根据图表信息,解答下列问题:
(1)、本次调查的学生总人数为 , 表中的值为;(2)、该校共有500名学生,请你估计等级为的学生人数;(3)、本次调查中,等级为的4人中有两名男生和两名女生,若从中随机抽取两人进行活动感想交流,请利用画树状图或列表的方法,求恰好抽到一名男生和一名女生的概率.21. 已知一次函数的图象与反比例函数的图象相交于点 , . (1)、求一次函数的表达式,并在图中画出这个一次函数的图象;(2)、根据函数图象,直接写出不等式的解集.22. 如图,在中, , 是边上一点,以为圆心,为半径的圆与相交于点 , 连接 , 且 .
(1)、求一次函数的表达式,并在图中画出这个一次函数的图象;(2)、根据函数图象,直接写出不等式的解集.22. 如图,在中, , 是边上一点,以为圆心,为半径的圆与相交于点 , 连接 , 且 . (1)、求证:是的切线;(2)、若 , , 求的长.23. 如图1是一架菱形风筝,它的骨架由如图2的4条竹棒AC,BD,EF,GH组成,其中E,F,G,H分别是菱形四边的中点,现有一根长为的竹棒,正好锯成风筝的四条骨架,设菱形的面积为.
(1)、求证:是的切线;(2)、若 , , 求的长.23. 如图1是一架菱形风筝,它的骨架由如图2的4条竹棒AC,BD,EF,GH组成,其中E,F,G,H分别是菱形四边的中点,现有一根长为的竹棒,正好锯成风筝的四条骨架,设菱形的面积为.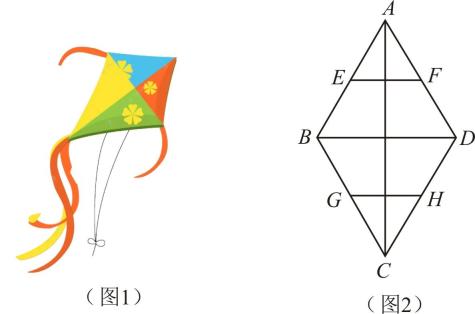 (1)、写出y关于的函数关系式:(2)、为了使风筝在空中有较好的稳定性,要求 , 那么当骨架的长为多少时,这风筝即菱形的面积最大?此时最大面积为多少?24. 如图,一次函数 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)、写出y关于的函数关系式:(2)、为了使风筝在空中有较好的稳定性,要求 , 那么当骨架的长为多少时,这风筝即菱形的面积最大?此时最大面积为多少?24. 如图,一次函数 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点. (1)、求这个抛物线的解析式;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)、在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.25. 如图1,在中,于点D,在DA上取点E,使 , 连接BE、CE.
(1)、求这个抛物线的解析式;(2)、作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)、在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.25. 如图1,在中,于点D,在DA上取点E,使 , 连接BE、CE.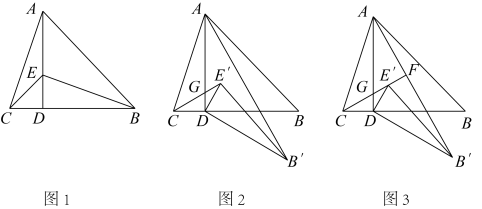 (1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.
(1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.