天津市西青区2023年中考一模数学试卷
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 计算的结果等于( )A、1 B、 C、 D、62. 的值等于( )A、 B、1 C、 D、3. 春暖花开,城市按下快进键,天津地铁客流持续增长,2023年2月25日客运量达到1853000人次,截止当天该客运量创近3年新高.将1853000用科学记数法表示应为( )A、 B、 C、 D、4. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 右图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
5. 右图是一个由6个相同的正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、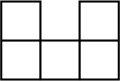 C、
C、 D、
D、 6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 方程组的解是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,菱形的四个顶点都在坐标轴上,且菱形边长为2, , 则点的坐标为( )
6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 方程组的解是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,菱形的四个顶点都在坐标轴上,且菱形边长为2, , 则点的坐标为( ) A、 B、 C、 D、9. 计算的结果是( )A、 B、 C、3 D、210. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、11. 如图,在中, , , 将绕点逆时针旋转60°得到 , 点 , 的对应点分别为 , , 连接交于点 , 下列结论一定正确的是( )
A、 B、 C、 D、9. 计算的结果是( )A、 B、 C、3 D、210. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、11. 如图,在中, , , 将绕点逆时针旋转60°得到 , 点 , 的对应点分别为 , , 连接交于点 , 下列结论一定正确的是( ) A、 B、 C、 D、12. 已知抛物线( , , 是常数, , )对称轴为 , 且经过点 . 下列结论:
A、 B、 C、 D、12. 已知抛物线( , , 是常数, , )对称轴为 , 且经过点 . 下列结论:①;
②;
③关于的方程恰好有两个相等的实数根,则 .
其中,正确的个数是( )
A、3 B、2 C、1 D、0二、填空题
-
13. 计算的结果等于 .14. 计算 的结果等于 .15. 不透明袋子中装有8个球,其中有3个红球、5个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .16. 将直线向下平移2个单位长度,平移后直线的解析式为 .17. 如图,点是正方形中延长线上一点,连接 , 点是的中点,连接 , 若 , , 则的长为 .

三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中,点 , , 均落在格点上,连接 , .
 (1)、线段的长等于 .(2)、以为圆心,为半径作圆,在上找一点 , 满足 . 请用无刻度的直尺,在如图所示的网格中,画出点 , 作出 , 并简要说明点的位置是如何找到的.19. 解不等式组
(1)、线段的长等于 .(2)、以为圆心,为半径作圆,在上找一点 , 满足 . 请用无刻度的直尺,在如图所示的网格中,画出点 , 作出 , 并简要说明点的位置是如何找到的.19. 解不等式组请结合题意填空,完成本题的解答.
 (1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来(4)、原不等式组的解集为 .20. 某中学为加强学生的劳动教育,需要制定学生每周劳动实践(单位:小时)的合格标准,为此随机调查了若干名学生目前每周劳动时间,获得数据并整理,绘制出如下的统计图①和图②.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来(4)、原不等式组的解集为 .20. 某中学为加强学生的劳动教育,需要制定学生每周劳动实践(单位:小时)的合格标准,为此随机调查了若干名学生目前每周劳动时间,获得数据并整理,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)、本次接受调查的学生人数为人,图①中的值为;(2)、求统计的这部分学生每周劳动时间的平均数、众数和中位数.21. 已知是的直径,点 , 是上两点, , 连接 , , . (1)、如图①,若 , , 求和的大小;(2)、如图②,过点作的切线,与的延长线交于点 , 若 , 求的大小.22. 如图,一艘货船在灯塔的正南方向,距离灯塔海里的处遇险,发出求救信号.一艘救生船位于灯塔的南偏东40°方向上,同时位于处的北偏东45°方向上的处,救生船接到求救信号后,立即前往救援.求的长(结果取整数).参考数据: , 取 .
(1)、如图①,若 , , 求和的大小;(2)、如图②,过点作的切线,与的延长线交于点 , 若 , 求的大小.22. 如图,一艘货船在灯塔的正南方向,距离灯塔海里的处遇险,发出求救信号.一艘救生船位于灯塔的南偏东40°方向上,同时位于处的北偏东45°方向上的处,救生船接到求救信号后,立即前往救援.求的长(结果取整数).参考数据: , 取 . 23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小明家、体育场、文具店在同一直线上,体育场离小明家2.5 , 文具店离小明家1.5 . 小明从家出发跑步15到达体育场,在体育场锻炼了15后,又走了15到文具店购买文具,然后走回家.给出的图象反映了这个过程中小明离家的距离与离开家的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开家的时间/
6
9
20
30
50
离家的距离/
1
2.5
(2)、填空:①体育场到文具店的距离为;
②小明在文具店购买文具所用的时间;
③小明从文具店走回家的速度为;
④当小明离家的距离为1.7时,他离开家的时间为 .
(3)、当时,请直接写出关于的函数解析式.24. 在平面直角坐标系中,为原点,是等腰直角三角形, , , 点在轴的负半轴上,点在第二象限,矩形的顶点 , 点在轴的正半轴上,点在轴的正半轴上.将沿轴向右平移,得到 , 点 , , 的对应点分别为 , , . (1)、如图1,当经过点时,求点的坐标;(2)、设 , 与矩形重叠部分的面积为;
(1)、如图1,当经过点时,求点的坐标;(2)、设 , 与矩形重叠部分的面积为;①如图②,当与矩形重叠部分为五边形时,与相交于点 , 分别与 , 交于点 , , 试用含有的式子表示 , 并直接写出的取值范围;
②请直接写出满足的所有的值.
25. 已知抛物线(为常数,)的顶点为 .(1)、当时,求该抛物线顶点的坐标;(2)、若该抛物线与轴交于点 , (点在点左侧),与轴交于点 .①点是该抛物线对称轴上一个动点,当的最小值为时,求该抛物线的解析式和点的坐标.
②连接 , 与抛物线的对称轴交于点 , 过点作 , 垂足为 , 若 , 求该抛物线的解析式.