山西省忻州市原平市2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. -6的绝对值为( )A、 B、 C、 D、
-
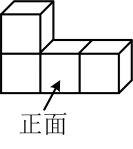
2. 如图所示的是由4个大小相同的小正方体搭建而成的几何体,则该几何体的左视图为( )
 A、
A、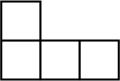 B、
B、 C、
C、 D、
D、
-
3. 2022年12月26日是伟大领袖毛主席诞辰129周年纪念日,伟人在他的诗词中写道“坐地日行八万里,巡天遥看一千河”,那么数据“八万里”用科学记数法可表示为( )A、里 B、里 C、里 D、里
-
4. 下列运算正确的是( )A、 B、 C、 D、
-
5. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上,若线段 , 则线段的长是( )
 A、 B、 C、 D、2
A、 B、 C、 D、2 -
6. 将不等式组的解集在数轴上表示,正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
7. 小明坚持每天进行体育锻炼,如表是小明近一周的体育锻炼时间表:
日期
时间(分钟)
则这组数据的中位数和众数分别是( )
A、 , B、 , C、 , D、 , -
8. 如图,点A,B,C均在⊙O上,若 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 在2023年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度y(单位:米)与飞行的水平距离x(单位:米)之间具有函数关系 , 则小康这次实心球训练的成绩为( )
 A、14米 B、12米 C、11米 D、10米
A、14米 B、12米 C、11米 D、10米 -
10. 如图,四边形是菱形, , , 扇形的半径为4,圆心角为 , 则图中阴影部分的面积是( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 计算: =
-
12. 如图所示的是一组有规律的图案,则第n个图案中“
 ”的个数为 . (用含n的代数式表示)
”的个数为 . (用含n的代数式表示)
-
13. 如图,直线与反比例函数的图象交于点A,B,与x轴交于点D,过点A作轴于点C,若 , 则k= .

-
14. 年元旦期间,小华和家人到汾河公园景区游玩,湖边有大小两种游船,小华发现:2艘大船与3艘小船一次共可以满载游客60人,1艘大船与1艘小船一次共可以满载游客人.则1艘大船可以满载游客的人数为 .

-
15. 如图,在菱形中,边长为 , , E,F分别是边上的点,且 , 若将沿着折叠,使得点B恰好落在边上的点处, , 折痕为 , 则的长为 .

三、解答题
-
16.(1)、计算:;(2)、解方程: .
-
17. 如图,在中, .
 (1)、以为直径,利用尺规作交于点D.(要求:尺规作图并保留作图痕迹,不写作法,标明字母)(2)、在(1)中所作的图中,若 , , 求的半径.
(1)、以为直径,利用尺规作交于点D.(要求:尺规作图并保留作图痕迹,不写作法,标明字母)(2)、在(1)中所作的图中,若 , , 求的半径. -
18. 布艺手袋因节能时尚,成为学生一族的新宠.该商店用1200元购进第一批布艺手袋,很快售罄,于是又花费4500元购进第二批布艺手袋,所购数量是第一批的2倍,已知第二批布艺手袋的单价比第一批布艺手袋的单价贵7元,求第一批购进的布艺手袋的单价.

-
19. 为了贯彻落实国务院提出的“健康第一”的指导思想,切实加强学校体育工作,使学生养成良好的锻炼习惯,提高学生体质的健康水平,《国家中学生体质健康标准》规定学生体质健康等级标准如表:
等级
A:优秀
B:良好
C:及格
D:不及格
分数(x/分)
太原市某校从九年级学生中随机抽取了400名学生进行了体质测试,将调查结果整理后绘制成如图所示的两幅统计图,根据统计图提供的信息解答下列问题:
 (1)、在这被抽查的九年级学生中,优秀的有人,及格的有人.(2)、求所抽取的400名学生的平均分.(3)、该校校委会决定从获得优秀奖成绩前三名学生中选取2名同学参加省体质测试,已知前三名学生中只有1名男生,请用列表或画树状图的方法求所选的2名学生恰好是1名男生和1名女生的概率.
(1)、在这被抽查的九年级学生中,优秀的有人,及格的有人.(2)、求所抽取的400名学生的平均分.(3)、该校校委会决定从获得优秀奖成绩前三名学生中选取2名同学参加省体质测试,已知前三名学生中只有1名男生,请用列表或画树状图的方法求所选的2名学生恰好是1名男生和1名女生的概率. -
20. 阅读与思考.
纯几何法验证勾股定理我们知道,勾股定理:在直角三角形中,两条直角边的平方和等于斜边的平方.勾股定理的验证方法到目前为止也有300多种,最著名的有“赵爽弦图法”“总统证法”“毕达哥拉斯法”“青朱出入法”“达·芬奇法”“欧几里得法”等等.下面我们介绍一种纯几何验证法.
如图1,在中, , 于点D,先证明 , 可得 , 再证明 , 可得 , 两式相加即可得勾股定理,这种方法避开了利用拼图和面积法繁琐的证明,不失为一种很好的验证方法.
阅读下列材料,并完成相应的任务.
 (1)、根据材料中的方法,请写出完整的证明过程.(2)、如图2,将直角三角形分割成一个正方形和两对全等的直角三角形,我们把这样的直角三角形称为“勾股形”,图3是由两个完全相同的“勾股形”拼接而成的矩形,若 , 求该矩形的面积.
(1)、根据材料中的方法,请写出完整的证明过程.(2)、如图2,将直角三角形分割成一个正方形和两对全等的直角三角形,我们把这样的直角三角形称为“勾股形”,图3是由两个完全相同的“勾股形”拼接而成的矩形,若 , 求该矩形的面积. -
21. 如图1所示的是一种太阳能路灯,它由灯杆和灯管支架两部组成,图2是它的简易平面图.小明想知道灯管距地面的高度,他在地面处测得灯管的仰角为 , 在地面处测得在灯管仰角为 , 并测得 , 已知点 , , 在同一条直线上,请根据以上数据帮小明算出灯管距地面的高度(结果精确到 , 参考数据: , , ).

-
22.(1)、综合与实践
问题情境:如图1,在中, , , D,E分别是 , 的中点,连接 .

如图2,将绕着点C逆时针旋转 , 连接BE和 , 小明发现 , , 请你证明该结论.
(2)、猜想探究:如图3,将绕着点C逆时针旋转 , 此时恰好有 , 连接 , 延长 , 交于点F,试猜想四边形的形状,并说明理由.
拓展探究:
(3)、如图4,将绕着点C逆时针旋转 , 直接写出四边形的面积的最大值. -
23. 综合与探究.
如图1,抛物线经过 , , 且与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,连接 , .
 (1)、求抛物线的表达式.(2)、求证: .(3)、如图2,动点P从点B出发,沿着线段以每秒1个单位长度的速度向终点A运动;同时,动点Q从点A出发,以相同的速度沿着线段向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动,连接 , 设P,Q运动的时间为t秒,在点P,Q运动的过程中,是否成为等腰三角形?若能,请求出t的值;若不能,请说明理由.
(1)、求抛物线的表达式.(2)、求证: .(3)、如图2,动点P从点B出发,沿着线段以每秒1个单位长度的速度向终点A运动;同时,动点Q从点A出发,以相同的速度沿着线段向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动,连接 , 设P,Q运动的时间为t秒,在点P,Q运动的过程中,是否成为等腰三角形?若能,请求出t的值;若不能,请说明理由.
