山东省淄博市周村区周村2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 下列实数中,无理数是( )A、 B、 C、 D、2. 下列图案,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 上网搜索“淄博烧烤”,网页显示找到相关结果约31600000个.数据31600000用科学记数法表示为( )A、 B、3.16×106 C、3.16×107 D、31.6×1064. 下列运算正确的是( )A、(﹣2a3)2=4a6 B、a2•a3=a6 C、3a+a2=3a3 D、(a﹣b)2=a2﹣b25. 化简 + 的结果是( )A、x﹣2 B、 C、 D、6. 如图,线段是的直径,C,D为上两点,如果 , 那么的度数是( )
3. 上网搜索“淄博烧烤”,网页显示找到相关结果约31600000个.数据31600000用科学记数法表示为( )A、 B、3.16×106 C、3.16×107 D、31.6×1064. 下列运算正确的是( )A、(﹣2a3)2=4a6 B、a2•a3=a6 C、3a+a2=3a3 D、(a﹣b)2=a2﹣b25. 化简 + 的结果是( )A、x﹣2 B、 C、 D、6. 如图,线段是的直径,C,D为上两点,如果 , 那么的度数是( ) A、 B、 C、 D、7. 有一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )
A、 B、 C、 D、7. 有一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )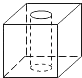 A、
A、 B、
B、 C、
C、 D、
D、 8. 每年的4月23日为“世界读书日”,某学校为了鼓励学生多读书,开展了“书香校园”的活动.如图是初三某班班长统计的全班50名学生一学期课外图书的阅读量(单位:本),则这50名学生图书阅读数量的中位数,众数和平均数分别是( )
8. 每年的4月23日为“世界读书日”,某学校为了鼓励学生多读书,开展了“书香校园”的活动.如图是初三某班班长统计的全班50名学生一学期课外图书的阅读量(单位:本),则这50名学生图书阅读数量的中位数,众数和平均数分别是( ) A、18,12,12 B、12,12,12 C、15,12,14.8 D、15,10,14.59. 如图,在矩形中,过点D作对角线的垂线,垂足为E,过点E作的垂线交于点F,如果 , , 那么的长是( )
A、18,12,12 B、12,12,12 C、15,12,14.8 D、15,10,14.59. 如图,在矩形中,过点D作对角线的垂线,垂足为E,过点E作的垂线交于点F,如果 , , 那么的长是( ) A、3 B、 C、 D、10. 如图,在平面直角坐标系中,点A,B都在反比例函数的图象上,且是等边三角形,若 , 则k的值为( )
A、3 B、 C、 D、10. 如图,在平面直角坐标系中,点A,B都在反比例函数的图象上,且是等边三角形,若 , 则k的值为( )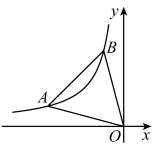 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:-1-2= .12. 某人连续抛掷一枚质地均匀的硬币10次,结果都是正面朝上,则他第11次抛掷这枚硬币,正面朝上的概率是 .13. 如图,在▱ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为 .
 14. 魏晋时期,数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理,其中四边形、四边形和四边形都是正方形.如果图中与的面积比为 , 那么的值为 .
14. 魏晋时期,数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理,其中四边形、四边形和四边形都是正方形.如果图中与的面积比为 , 那么的值为 . 15. 如图,O为坐标原点,点在y轴的正半轴上,点在函数位于第一象限的图象上,若 , , , …,都是等边三角形,则线段的长是 .
15. 如图,O为坐标原点,点在y轴的正半轴上,点在函数位于第一象限的图象上,若 , , , …,都是等边三角形,则线段的长是 .
三、解答题
-
16. 已知 求下列各式的值:(1)、 ;(2)、 .17. 如图,中, , .
 (1)、求的长:(2)、是边上的高,请你补全图形,并求的长.18. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)、求的长:(2)、是边上的高,请你补全图形,并求的长.18. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.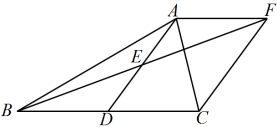 (1)、求证:D是BC的中点;(2)、如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论.19. 某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)、求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)、学校计划租用甲、乙两种客车共8辆,甲种客车每辆载客量45人,乙种客车每辆载客量30人,共有师生330人,求最节省的租车费用是多少元?20. 如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC, .
(1)、求证:D是BC的中点;(2)、如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论.19. 某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)、求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)、学校计划租用甲、乙两种客车共8辆,甲种客车每辆载客量45人,乙种客车每辆载客量30人,共有师生330人,求最节省的租车费用是多少元?20. 如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC, .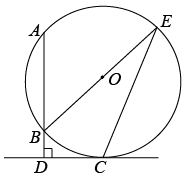 (1)、求证:CD是⊙O的切线;(2)、若 , , 求AB的长.21. 如图,双曲线y=上的一点A(m,n),其中n>m>0,过点A作AB⊥x轴于点B,连接OA.
(1)、求证:CD是⊙O的切线;(2)、若 , , 求AB的长.21. 如图,双曲线y=上的一点A(m,n),其中n>m>0,过点A作AB⊥x轴于点B,连接OA. (1)、已知△AOB的面积是3,求k的值;(2)、将△AOB绕点A逆时针旋转90°得到△ACD,且点O的对应点C恰好落在该双曲线上,求的值.22. 如图,在正方形中,E是边上的一点,过点E作的垂线交于点P,交于点F,连接并延长交于点G.
(1)、已知△AOB的面积是3,求k的值;(2)、将△AOB绕点A逆时针旋转90°得到△ACD,且点O的对应点C恰好落在该双曲线上,求的值.22. 如图,在正方形中,E是边上的一点,过点E作的垂线交于点P,交于点F,连接并延长交于点G. (1)、求证:;(2)、若 , 求的度数;(3)、若 , , 求的面积.23. 抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B,C的坐标分别为(4,0)和(0,4),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
(1)、求证:;(2)、若 , 求的度数;(3)、若 , , 求的面积.23. 抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B,C的坐标分别为(4,0)和(0,4),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m). (1)、求抛物线和直线AD的解析式;(2)、如图Ⅰ,点Q是线段AB上一动点,过点Q作QE∥AD,交BD于点E,连接DQ,求△QED面积的最大值;(3)、如图Ⅱ,直线AD交y轴于点F,点M,N分别是抛物线对称轴和抛物线上的点,若以C,F,M,N为顶点的四边形是平行四边形,求点M的坐标.
(1)、求抛物线和直线AD的解析式;(2)、如图Ⅰ,点Q是线段AB上一动点,过点Q作QE∥AD,交BD于点E,连接DQ,求△QED面积的最大值;(3)、如图Ⅱ,直线AD交y轴于点F,点M,N分别是抛物线对称轴和抛物线上的点,若以C,F,M,N为顶点的四边形是平行四边形,求点M的坐标.