山东省淄博市桓台县2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下面几何体中,是圆锥的为( )A、
 B、
B、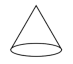 C、
C、 D、
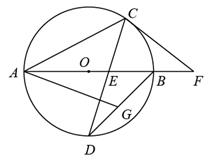
D、 3. 年月日工业和信息化部负责人在“世界电信和信息社会日”大会上宣布,我国目前已建成基站近万个,成为全球首个基于独立组网模式规模建设网络的国家,将数据万用科学记数法表示为( )A、 B、 C、 D、4. 如图,.若 , 则的大小为( )
3. 年月日工业和信息化部负责人在“世界电信和信息社会日”大会上宣布,我国目前已建成基站近万个,成为全球首个基于独立组网模式规模建设网络的国家,将数据万用科学记数法表示为( )A、 B、 C、 D、4. 如图,.若 , 则的大小为( )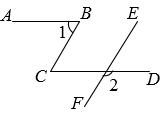 A、 B、 C、 D、5. 如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )
A、 B、 C、 D、5. 如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )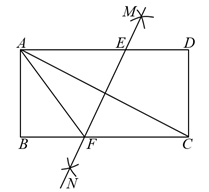 A、AF=CF B、∠FAC=∠EAC C、AB=4 D、AC=2AB6. 下面的三个问题中都有两个变量:
A、AF=CF B、∠FAC=∠EAC C、AB=4 D、AC=2AB6. 下面的三个问题中都有两个变量:①汽车匀速从A地行驶到B地,汽车的剩余路程y与行驶时间x;
②用长度一定的绳子围成一个矩形,矩形的面积y与一边长x;
③将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
其中,变量y与变量x之间的函数关系可以用如图所示的图象表示的是( )
 A、①② B、①③ C、②③ D、①②③7. 如图,正六边形内接于 , 若的周长等于 , 则正六边形的面积为( )
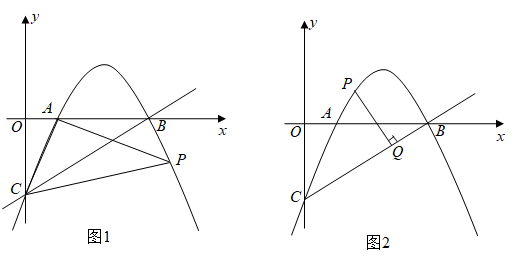
A、①② B、①③ C、②③ D、①②③7. 如图,正六边形内接于 , 若的周长等于 , 则正六边形的面积为( ) A、 B、 C、 D、8. 如图,二次函数的图象与轴交于点 , 两点,对称轴是直线 , 下列说法正确的是( )
A、 B、 C、 D、8. 如图,二次函数的图象与轴交于点 , 两点,对称轴是直线 , 下列说法正确的是( ) A、 B、当时,的值随的增大而增大 C、点的坐标为 D、9. 如图,点 , 点是轴正半轴上的一点,将线段绕点按逆时针方向旋转得到线段 , 若点的坐标为 , 则的值为( )
A、 B、当时,的值随的增大而增大 C、点的坐标为 D、9. 如图,点 , 点是轴正半轴上的一点,将线段绕点按逆时针方向旋转得到线段 , 若点的坐标为 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 规定:在平面直角坐标系中,一个点作“0”变换表示将它向右平移一个单位,一个点作“1”变换表示将它绕原点顺时针旋转90°,由数字0和1组成的序列表示一个点按照上面描述依次连续变换.例如:如图,点按序列“011…”作变换,表示点O先向右平移一个单位得到 , 再将绕原点顺时针旋转90°得到 , 再将绕原点顺时针旋转90°得到…依次类推.点经过“011011011”变换后得到点的坐标为 .
 11. 已知 , 则 .12. 在平面直角坐标系中,若点在反比例函数的图象上,则(填“>”“=”或“<”)13. 如图,和是以点为位似中心的位似图形.若 , 则与的周长比是 .
11. 已知 , 则 .12. 在平面直角坐标系中,若点在反比例函数的图象上,则(填“>”“=”或“<”)13. 如图,和是以点为位似中心的位似图形.若 , 则与的周长比是 .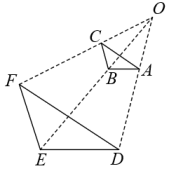 14. 化简 的结果是.15. 如图,将扇形AOB沿OB方向平移,使点O移到OB的中点 处,得到扇形 .若∠O=90°,OA=2,则阴影部分的面积为.
14. 化简 的结果是.15. 如图,将扇形AOB沿OB方向平移,使点O移到OB的中点 处,得到扇形 .若∠O=90°,OA=2,则阴影部分的面积为.
三、解答题
-
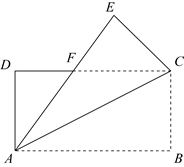
16. 解不等式组: , 并将其解集在数轴上表示出来.17. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.
 (1)、求证: ;(2)、若 ,求 的度数.18. 随着“公园城市”建设的不断推进,成都绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是 , 乙骑行的路程与骑行的时间之间的关系如图所示.
(1)、求证: ;(2)、若 ,求 的度数.18. 随着“公园城市”建设的不断推进,成都绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是 , 乙骑行的路程与骑行的时间之间的关系如图所示.
 (1)、直接写出当和时,与之间的函数表达式;(2)、何时乙骑行在甲的前面?19. 2022年6月6日是第27个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.如图,当张角时,顶部边缘处离桌面的高度的长为 , 此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角时(点是的对应点),用眼舒适度较为理想.求此时顶部边缘处离桌面的高度的长.(结果精确到;参考数据: , , )
(1)、直接写出当和时,与之间的函数表达式;(2)、何时乙骑行在甲的前面?19. 2022年6月6日是第27个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.如图,当张角时,顶部边缘处离桌面的高度的长为 , 此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角时(点是的对应点),用眼舒适度较为理想.求此时顶部边缘处离桌面的高度的长.(结果精确到;参考数据: , , )
 20. 如图,一次函数的图像与反比例函数的图像交于点 , 与y轴交于点B,与x轴交于点 .
20. 如图,一次函数的图像与反比例函数的图像交于点 , 与y轴交于点B,与x轴交于点 .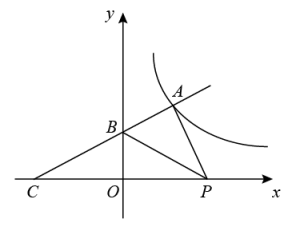 (1)、求k与m的值;(2)、为x轴上的一动点,当△APB的面积为时,求a的值.21. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)、求k与m的值;(2)、为x轴上的一动点,当△APB的面积为时,求a的值.21. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: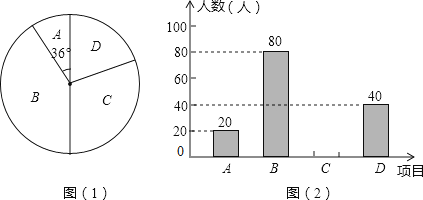 (1)、这次被调查的学生共有 人;
(1)、这次被调查的学生共有 人;
(2)、请你将条形统计图(2)补充完整;
(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率.(用树状图或列表法解答)