山东省泰安市泰山区2023年中考数学一模试题

试卷更新日期：2023-05-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 下面几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
2. 在实数： $- (- 6)$ ， $- 5$ ， 0， $| - 3 |$ 中，最小的数是（）

A、 $- (- 6)$ B、 $- 5$ C、0 D、 $| - 3 |$

查看试题解析
3. 截至2022年6月2日，世界第四大水电站——云南昭通溪洛渡水电站累计生产清洁电能突破5000亿千瓦时，相当于替代标准煤约1.52亿吨，减排二氧化碳约4.16亿.5000亿用科学记数法表示为（）

A、 $50 \times 1 0^{10}$ B、 $5 \times 1 0^{11}$ C、 $0.5 \times 1 0^{12}$ D、 $5 \times 1 0^{12}$

查看试题解析
4. 下列运算，结果等于 $a^{6}$ 的是（）

A、 $a + 5 a$ B、 $a^{2} \cdot a^{3}$ C、 ${(a^{2})}^{4}$ D、 $a^{8} \div a^{2}$

查看试题解析
5. 如图，三角形板的直角顶点落在矩形纸片的一边上，若 $∠ 1 = 55 °$ ，则 $∠ 2$ 的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
6. 为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据，如下表：
甲
4
8
9
9
10
乙
4
5
6
10
10
关于以上数据，说法正确的是（）

A、甲、乙的中位数相同 B、甲、乙的众数相同 C、甲的平均数小于乙的平均数 D、甲的方差小于乙的方差

查看试题解析
7. 如图， $⊙ O$ 的半径 $O B$ 为6，半径 $O C ⊥ A B$ 于点D， $∠ B A C = 30 °$ ，则 $C D$ 的长是（）

A、3 B、2 C、 $2 \sqrt{3}$ D、 $\sqrt{6}$

查看试题解析
8. 过直线l外一点P作直线l的垂线PQ．下列尺规作图错误的是（）

A、 B、 C、 D、

查看试题解析
9. 不等式组 ${\begin{array}{l} x < m \\ x \geq 3 \end{array}$ 有4个整数解，则m的取值范围是（）

A、 $6 \leq m \leq 7$ B、 $6 < m < 7$ C、 $6 \leq m < 7$ D、 $6 < m \leq 7$

查看试题解析
10. 如图， $A B$ 是 $⊙ O$ 的切线，B为切点， $C A$ 与 $⊙ O$ 交于点C，以点A为圆心、以 $O C$ 的长为半径，作 $\overset{⌢}{E F}$ ，分别交 $A B 、 B C$ 于点E、F．若 $O C = 3$ ， $A B = 6$ ，则图中阴影部分的面积为（）

A、 $9 - \frac{9}{4} π$ B、 $3 - \frac{9}{4} π$ C、 $4 - π$ D、 $2 - π$

查看试题解析
11. 如图，已知 $△ A B C$ ， $A B = A C$ ， $B C = 16$ ， $A D ⊥ B C$ ， $∠ A B C$ 的平分线交 $A D$ 于点E，且 $D E = 4$ ．将 $∠ C$ 沿 $G M$ 折叠，使点C与点E恰好重合，下列结论：① $D M = 4$ ， ②点E到 $A C$ 的距离为3，③ $E M = 5$ ， ④四边形 $C G E M$ 是菱形．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列4个结论：① $a b c > 0$ ；② $b^{2} < 4 a c$ ；③ $2 c < 3 b$ ；④ $a + b \geq m (a m + b)$ ；其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $3 x^{2} - 12 y^{2} =$ .

查看试题解析
14. 不透明布袋中装有除颜色外没有其他区别的2个红球和3个白球，搅匀后从中摸出一个球，放回搅匀，再摸出一个球，两次都摸出白球的概率是．

查看试题解析
15. 我国古代《四元玉鉴》中记载二果问价问题，其内容如下：九百九十九文钱，甜果苦果买千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？其意思为：九百九十九文钱买了甜果和苦果共一千个．已知十一文钱可买九个甜果，四文钱可买七个苦果，那么甜果、苦果各买了多少个？买甜果和苦果各需要多少文钱？若设买甜果x个，买苦果y个，根据题意所列方程组是．

查看试题解析

三、解答题

16. 数学活动小组到某广场测量标志性建筑 $A B$ 的高度．如图，他们在地面上C点测得最高点A的仰角为 $22 °$ ，再向前 $70 m$ 至 $D$ 点，又测得最高点 $A$ 的仰角为 $58 °$ ，点 $C$ ， $D$ ， $B$ 在同一直线上，则该建筑物 $A B$ 的高度约为多少？（精确到 $1 m$ ．参考数据： $s i n 22 ° \approx 0.37$ ， $t a n 22 ° \approx 0.40$ ， $s i n 58 ° \approx 0.85$ ， $t a n 58 ° \approx 1.60$ ）

查看试题解析

四、填空题

17. 根据图中数字的规律，则 $x + y$ 的值是．

查看试题解析
18. 如图，菱形 $A B C D$ 的对角线相交于点O， $A C = 6$ ， $B D = 8$ ，点P为边 $B C$ 上一点，且P不与B、C重合．过P作 $P E ⊥ A C$ 于E， $P F ⊥ B D$ 于F，连接 $E F$ ，则 $E F$ 的最小值等于．

查看试题解析

五、解答题

19.

(1)、先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x^{2} - x}{x^{2} + 2 x + 1}$ ，其中 $x = \sqrt{2} + 1$ ．

(2)、解不等式组： ${\begin{array}{l} x + 2 > \frac{3 x - 1}{2} ① \\ 2 x - (x - 3) \geq 5 ② \end{array}$ ，并把它们的解集在数轴上表示出来．

查看试题解析
20. 某校为了响应市政府号召，在“创文明城市”活动周中，设置了“ $A$ ：文明礼仪， $B$ ：环境保护， $C$ ：卫生保洁， $D$ ：垃圾分类”四个主题，每个学生选一个主题参与．为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图：条形统计图和扇形统计图．

(1)、求本次调查的学生人数和 $m$ 的值；

(2)、请补全条形统计图；

(3)、学校要求每位同学从星期一至星期五选择两天参加活动．如果小明同学随机选择两天，那么其中有一天是星期五的概率是多少?

查看试题解析
21. 如图，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与正比例函数 $y = - 2 x$ 的图象相交于 $A (- 1 ， a)$ 、B两点，点C在第三象限， $B C ∥ x$ 轴．

(1)、求反比例函数的表达式；

(2)、以 $A B 、 B C$ 为边作菱形 $A B C D$ ，求D点坐标．

查看试题解析
22. 如图，四边形 $A B C D$ 是 $⊙ O$ 的内接四边形，连接 $A C ， B D ，$ 延长 $C D$ 至点E．

(1)、若 $A B = A C$ ，求证： $A D$ 平分 $∠ B D E$ ；

(2)、若 $B C = 4$ ， $⊙ O$ 的半径为6，求 $c o s ∠ B A C$ ．

查看试题解析
23. 某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求，决定增设篮球，足球两门选修课程，需要购进一批篮球和足球．若购买篮球的数量是足球的2倍，购买篮球用了6000元，购买足球用了2000元，篮球单价比足球单价贵30元；

(1)、求篮球和足球的单价分别是多少元；

(2)、学校计划采购篮球、足球共60个，并要求篮球多于40个，且总费用低于5000元．那么有哪几种购买方案?

查看试题解析
24. 次函数 $y = a x^{2} + b x + 2$ 的图象交x轴于点A（－1，0），B（4，0），两点，交y轴于点C，动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．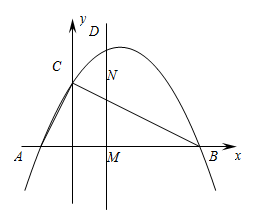

(1)、求二次函数 $y = a x^{2} + b x + 2$ 的表达式；

(2)、连接BD，当 $t = \frac{3}{2}$ 时，求△DNB的面积；

(3)、在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点P的坐标．

查看试题解析
25. 问题：如图，在 $▱ A B C D$ 中， $A B = 9$ ， $A D = 6$ ， $∠ D A B$ ， $∠ A B C$ 的平分线 $A E ， B F$ 分别与直线 $C D$ 交于点E，F．

(1)、求 $E F$ 的长．

(2)、把“问题”中的条件“ $A B = 9$ ”去掉，其余条件不变．当点E与点C重合时，求 $E F$ 的长．

(3)、把“问题”中的条件“ $A B = 9$ ， $A D = 6$ ”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求 $\frac{A D}{A B}$ 的值．

查看试题解析

甲	4	8	9	9	10
乙	4	5	6	10	10