山东省青岛市莱西2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. -7的相反数是( )A、7 B、-7 C、 D、2. 下列图形:

其中轴对称图形的个数是( )
A、4 B、3 C、2 D、13. 下列运算正确的是( )A、 B、 C、 D、4. 休闲广场供游客休息的石板凳如图所示,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
5. 如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )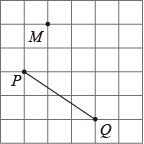 A、(2,3) B、(3,3) C、(4,2) D、(5,1)6. 如图,是的两条直径,E是劣弧的中点,连接 , . 若 , 则的度数为( )
A、(2,3) B、(3,3) C、(4,2) D、(5,1)6. 如图,是的两条直径,E是劣弧的中点,连接 , . 若 , 则的度数为( )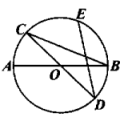 A、 B、 C、 D、7. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O.E,F 分别为 AC,BD 上一点,且 OE=OF,连接 AF,BE,EF,若∠AFE=25°,则∠CBE 的度数为( )
A、 B、 C、 D、7. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O.E,F 分别为 AC,BD 上一点,且 OE=OF,连接 AF,BE,EF,若∠AFE=25°,则∠CBE 的度数为( ) A、50° B、55° C、65° D、70°8. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A、50° B、55° C、65° D、70°8. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )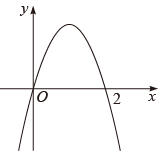 A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<0
A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<0二、填空题
-
9. 中国共产主义青年团是中国共产党领导的先进青年的群团组织,是中国共产党的助手和后备军.据中国共青团团内统计公报:截至2021年12月31日,全国共有共青团员7371.5万名,其中学生团员4381万名.将4381万用科学记数法表示为 .10. 与最接近的整数是 .11. 在“书香校园”读书活动中,随即调查了100名学生一个月内读书的本数如下表所示.
读书本数
1
2
3
4
5
学生数
x
30
20
16
4
则每名学生一个月的平均读书本数为本.
12. 如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线恰好经过B点,若 , , 则等于 . 13. 如图,在中, , 若将绕点顺时针旋转 , 点的对应点为点 , 点的对应点为点 , 点为的中点,连接 . 则点的运动路径与线段、围成的阴影部分面积是 .
13. 如图,在中, , 若将绕点顺时针旋转 , 点的对应点为点 , 点的对应点为点 , 点为的中点,连接 . 则点的运动路径与线段、围成的阴影部分面积是 . 14. 已知抛物线的图象与x轴相交于点A和点 , 与y轴交于点C,连接 , 有一动点D在线段上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F, , 设点D的横坐标为m.连接 , 则的最大面积为 .
14. 已知抛物线的图象与x轴相交于点A和点 , 与y轴交于点C,连接 , 有一动点D在线段上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F, , 设点D的横坐标为m.连接 , 则的最大面积为 .
三、解答题
-
15. 已知:如图,A、B、C三个点.求作: , 使经过A、B、C三点.
 16.(1)、化简:(2)、解不等式组17. 为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息解答下列问题:
16.(1)、化简:(2)、解不等式组17. 为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息解答下列问题:竞赛成绩统计表
组别
分数
人数
A组
4
B组
C组
10
D组
E组
14
竞赛成绩扇形统计图
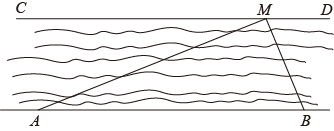
 (1)、本次共调查了名学生;(2)、C组所在扇形的圆心角为度;(3)、该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?18. “用可以再生的血液,挽救无法重来的生命”.某单位开展“世界献血日”自愿义务献血活动,参与献血者的血型有“A、B、、O”四种类型.现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.19. 小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.他先在河岸设立A,B两个观测点,然后选定对岸河边的一棵树记为点M.测得AB=50m,∠MAB=22°,∠MBA=67°.请你依据所测数据求出这段河流的宽度(结果精确到0.1m).
(1)、本次共调查了名学生;(2)、C组所在扇形的圆心角为度;(3)、该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?18. “用可以再生的血液,挽救无法重来的生命”.某单位开展“世界献血日”自愿义务献血活动,参与献血者的血型有“A、B、、O”四种类型.现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.19. 小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.他先在河岸设立A,B两个观测点,然后选定对岸河边的一棵树记为点M.测得AB=50m,∠MAB=22°,∠MBA=67°.请你依据所测数据求出这段河流的宽度(结果精确到0.1m).参考数据:sin22°≈ , cos22°≈ , tan22°≈ , sin67°≈ , cos67°≈ , tan67°≈ .
 20. 如图,正比例函数的图像与反比例函数的图像都经过点 .
20. 如图,正比例函数的图像与反比例函数的图像都经过点 . (1)、求点A的坐标和反比例函数表达式.(2)、若点在该反比例函数图象上,且它到y轴距离小于3,请根据图像直接写出n的取值范围.21. 某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)、求点A的坐标和反比例函数表达式.(2)、若点在该反比例函数图象上,且它到y轴距离小于3,请根据图像直接写出n的取值范围.21. 某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.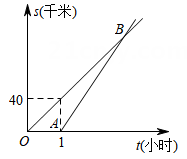 (1)、求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)、如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)、假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.22. 四边形为矩形,E是延长线上的一点, .
(1)、求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)、如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)、假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.22. 四边形为矩形,E是延长线上的一点, . (1)、求证:;(2)、添加一个条件 , 矩形为正方形.请说明理由.23.(1)、【问题呈现】
(1)、求证:;(2)、添加一个条件 , 矩形为正方形.请说明理由.23.(1)、【问题呈现】如图1,和都是等边三角形,连接 . 求证: .
 (2)、【类比探究】
(2)、【类比探究】如图2,和都是等腰直角三角形, . 连接 . 请直接写出的值.
(3)、【拓展提升】如图3,和都是直角三角形, , 且 . 连接 . 延长交于点F,交于点G.求的值.
24. 某公司电商平台经销一种益智玩具,先用元购进一批.售完后,第二次购进时,每件的进价提高了 , 同样用3000元购进益智玩具的数量比第一次少了25件.销售时经市场调查发现,该种益智玩具的周销售量y(件)是关于售价x(元/件)的一次函数,如表仅列出了该商品的售价x(元/件),周销售量y(件)的三组对应值数据.x
40
70
90
y
180
90
30
(1)、求第一次每件玩具的进价;(2)、求y关于x的函数解析式;(3)、售价x为多少时,第一周的销售利润W最大?并求出此时的最大利润.25. 如图,在四边形中, , , , 点P、Q分别是线段和上的动点.点P以的速度从点D向点C运动,同时点Q以的速度从点A向点D运动,当其中一点到达终点时,两点停止运动,将沿翻折得到 , 连接交直线于点E,连接 . 设运动时间为 , 回答下列问题: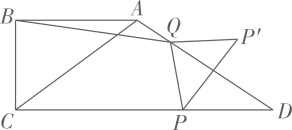 (1)、当t为何值时,?(2)、求四边形的面积关于时间的函数关系式;(3)、是否存在某时刻t,使点Q在平分线上?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,?(2)、求四边形的面积关于时间的函数关系式;(3)、是否存在某时刻t,使点Q在平分线上?若存在,求出t的值;若不存在,请说明理由.