山东省青岛市城阳区2023年九年级中考一模数学试卷
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列图形中,是轴对称图形且对称轴条数最多的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( )
3. 如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、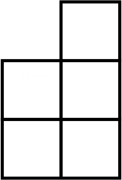 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,切于点C, , 的半径为 , , 则( ) .
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,切于点C, , 的半径为 , , 则( ) . A、6 B、 C、 D、6. 一车间有甲、乙两个小组,甲组的工作效率是乙组的2.5倍,因此加工3000个零件所用的时间乙组比甲组多1.5小时,若设乙组每小时加工x个零件,则可列方程为( )A、 B、 C、 D、7. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为6,则k的值是( )
A、6 B、 C、 D、6. 一车间有甲、乙两个小组,甲组的工作效率是乙组的2.5倍,因此加工3000个零件所用的时间乙组比甲组多1.5小时,若设乙组每小时加工x个零件,则可列方程为( )A、 B、 C、 D、7. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为6,则k的值是( )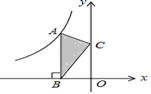 A、6 B、﹣6 C、12 D、﹣128. 已知,抛物线在平面直角坐标系中的位置如图,则一次函数与反比例函数在同一直角坐标系中的图象大致是( )
A、6 B、﹣6 C、12 D、﹣128. 已知,抛物线在平面直角坐标系中的位置如图,则一次函数与反比例函数在同一直角坐标系中的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算: .10. 未来年,我区将投资元,分三阶段建设所中小学.全面提高育人环境,全面提高办学水平,将用科学记数法表示为 .11. 质检部门从甲,乙两个厂家生产的同一种产品中,各抽出8件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
甲:3,4,5,6,7,7,8,8;乙:4,6,6,6,8,9,12,13.
已知两个厂家在广告中都称该种产品的使用寿命是6年.请根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一种特征数?
甲: , 乙: .
12. 如图,在中,D,E分别是的中点,F是线段上一点,连接 . 若 , , , 则的长为 . 13. 如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,AC,AB.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为2π,那么这个曲边三角形的面积是.
13. 如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,AC,AB.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为2π,那么这个曲边三角形的面积是.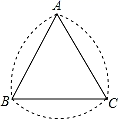 14. 如图,在中, , , , 点D、点E、点F分别是 , , 边的中点,连接、 , 得到 , 它的面积记作S;点、点、点分别是 , , 边的中点,连接、 , 得到 , 它的面积记作 , 照此规律作下去,则 .
14. 如图,在中, , , , 点D、点E、点F分别是 , , 边的中点,连接、 , 得到 , 它的面积记作S;点、点、点分别是 , , 边的中点,连接、 , 得到 , 它的面积记作 , 照此规律作下去,则 .
三、解答题
-
15. 已知: , 线段b.
求作: , 使 , , .
 16. 计算:(1)、解方程: .(2)、关于x的一元二次方程有实数根,求k的取值范围.17. 为响应国家提出由中国制造向中国创造转型的号召,某公司自主设计了一款机器人,每个生产成本为16元,投放市场进行了销售.经过调查,售价为30元/个时,每月可售出40万个,销售单价每涨价5元,每月就少售出10万个.(1)、确定月销售量y(万个)与售价x(元/个)之间的函数关系式;(2)、设商场每月销售这种机器人所获得的利润为w(万元),请确定所获利润w(万元)与售价x(元/个)之间的函数关系式 .18. 下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.
16. 计算:(1)、解方程: .(2)、关于x的一元二次方程有实数根,求k的取值范围.17. 为响应国家提出由中国制造向中国创造转型的号召,某公司自主设计了一款机器人,每个生产成本为16元,投放市场进行了销售.经过调查,售价为30元/个时,每月可售出40万个,销售单价每涨价5元,每月就少售出10万个.(1)、确定月销售量y(万个)与售价x(元/个)之间的函数关系式;(2)、设商场每月销售这种机器人所获得的利润为w(万元),请确定所获利润w(万元)与售价x(元/个)之间的函数关系式 .18. 下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并分别标记了数字1,2,3和1,2,3,4.小明和小亮利用这两个转盘做游戏.规则如下:同时转动两个转盘,指针停止后,将指针所指区域的数字相加(若指针停在分界线上,则重新转动转盘),如果和为奇数,则小明获胜,如果和是偶数,则小亮获胜,请你确定游戏规则是否公平,并说明理由.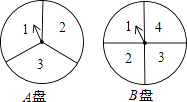 19. 某商店购进甲、乙两种手写笔进行销售,若售出2支甲种手写笔和1支乙种手写笔共收入354元,若售出3支甲种手写笔和2支乙种手写笔共收入600元.(1)、求甲、乙两种手写笔每支的售价是多少元?(2)、每支甲种手写笔的成本83元,每支乙种手写笔的成本103元.商店购进甲、乙两种手写笔共20支,其中乙种手写笔的数量不超过甲种手写笔数量的3倍,那么当购进甲、乙两种手写笔分别是多少支时,该商店销售完后获得利润最大?最大获利多少元?20. 月日是“世界粮食日”,某校倡导“光盘行动”,为了让学生养成珍惜粮食的优良习惯.在这天午餐后随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的条形统计图和扇形统计图:
19. 某商店购进甲、乙两种手写笔进行销售,若售出2支甲种手写笔和1支乙种手写笔共收入354元,若售出3支甲种手写笔和2支乙种手写笔共收入600元.(1)、求甲、乙两种手写笔每支的售价是多少元?(2)、每支甲种手写笔的成本83元,每支乙种手写笔的成本103元.商店购进甲、乙两种手写笔共20支,其中乙种手写笔的数量不超过甲种手写笔数量的3倍,那么当购进甲、乙两种手写笔分别是多少支时,该商店销售完后获得利润最大?最大获利多少元?20. 月日是“世界粮食日”,某校倡导“光盘行动”,为了让学生养成珍惜粮食的优良习惯.在这天午餐后随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的条形统计图和扇形统计图: (1)、把条形统计图补充完整.(2)、扇形统计图中,“剩大量”所对应的扇形的圆心角度数是°.(3)、为了树立良好的节约粮食风气,学校准备对全校“剩少量”和“没有剩”的同学颁发奖状,若全校共有2000名学生,则约有多少人获得奖状?21. 小明参观海军博物馆的军舰时,想测量一下军舰的长度.军舰停放位置平行于岸边主于道 , 军舰距离岸边主干道的距离是120米,由于军舰停放的位置正对的岸边是另一片展区,无法穿越,他想到借助于所学三角函数知识来测量计算,他沿平行于岸边的主干道从点C处走200米到点D处,在点C处测得军舰头部点A位于南偏东 , 在点D处测得军舰尾部点B位于南偏东 . 求军舰的长度(结果保留1位小数).( , , , )
(1)、把条形统计图补充完整.(2)、扇形统计图中,“剩大量”所对应的扇形的圆心角度数是°.(3)、为了树立良好的节约粮食风气,学校准备对全校“剩少量”和“没有剩”的同学颁发奖状,若全校共有2000名学生,则约有多少人获得奖状?21. 小明参观海军博物馆的军舰时,想测量一下军舰的长度.军舰停放位置平行于岸边主于道 , 军舰距离岸边主干道的距离是120米,由于军舰停放的位置正对的岸边是另一片展区,无法穿越,他想到借助于所学三角函数知识来测量计算,他沿平行于岸边的主干道从点C处走200米到点D处,在点C处测得军舰头部点A位于南偏东 , 在点D处测得军舰尾部点B位于南偏东 . 求军舰的长度(结果保留1位小数).( , , , ) 22. 如图,在中,点E、F分别在、上,且 , 直线与、的延长线分别交于点G、H.
22. 如图,在中,点E、F分别在、上,且 , 直线与、的延长线分别交于点G、H. (1)、求证:;(2)、连接、 , 若 , 请判断四边形的形状,并证明你的结论.23. 某农户家的菜地上有一个蔬菜大棚,其横截面顶部为抛物线型,现对其横截面建立如图所示的平面直角坐标系.大棚的一端固定在墙体离地面高米的点处,另一端固定在地面的点处,已知大棚上横截面抛物线顶部某点离地面的垂直高度(米)与其离墙体的水平距离(米)之间的关系满足 , 现测得点到墙体之间的水平距离为10米.
(1)、求证:;(2)、连接、 , 若 , 请判断四边形的形状,并证明你的结论.23. 某农户家的菜地上有一个蔬菜大棚,其横截面顶部为抛物线型,现对其横截面建立如图所示的平面直角坐标系.大棚的一端固定在墙体离地面高米的点处,另一端固定在地面的点处,已知大棚上横截面抛物线顶部某点离地面的垂直高度(米)与其离墙体的水平距离(米)之间的关系满足 , 现测得点到墙体之间的水平距离为10米. (1)、求抛物线的表达式;(2)、求大棚的最高点到地面的距离;(3)、该农户想在大棚横截面抛物线项部两侧,紧贴抛物线顶部安装照明灯,且照明灯到地面垂真高度为米,则两个照明灯的水平距离是多少米?24. 对于某些三角形,我们可以直接用面积公式或是用割补法等来求它们的面积,下面我们研究一种求面积的新方法:如图1所示,分别过三角形的顶点A、C作水平线的铅垂线、 , 、之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交于点D,称线段的长叫做这个三角形的铅垂高;
(1)、求抛物线的表达式;(2)、求大棚的最高点到地面的距离;(3)、该农户想在大棚横截面抛物线项部两侧,紧贴抛物线顶部安装照明灯,且照明灯到地面垂真高度为米,则两个照明灯的水平距离是多少米?24. 对于某些三角形,我们可以直接用面积公式或是用割补法等来求它们的面积,下面我们研究一种求面积的新方法:如图1所示,分别过三角形的顶点A、C作水平线的铅垂线、 , 、之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交于点D,称线段的长叫做这个三角形的铅垂高;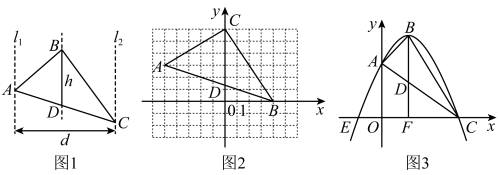
结论提炼:容易证明,“三角形的面积等于水平宽与铅垂高乘积的一半”,即“”.
尝试应用:
(1)、已知:如图2,点、、 , 则的水平宽为 , 铅垂高为 , 所以的面积为 .(2)、如图3,在平面直角坐标系中,抛物线的解析式为: , 点B为抛物线的顶点,图象与y轴交于点A,与x轴交于E、C两点,为的铅垂高,延长交x轴于点F,则顶点B坐标为 , 铅垂高 , 的面积为 .25. 已知:如图①,菱形中,对角线相交于点O,且 , . 点P从点A出发,沿方向匀速运动,速度为;同时,直线从点D出发,沿方向匀速运动,速度为 , , 且与分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接 , 设运动时间为 . 解答下列问题: (1)、当t为何值时,点A在线段的垂直平分线上?(2)、设四边形的面积为 , 求y与t之间的函数关系式;(3)、如图②,连接 , 是否存在某一时刻t,使?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,点A在线段的垂直平分线上?(2)、设四边形的面积为 , 求y与t之间的函数关系式;(3)、如图②,连接 , 是否存在某一时刻t,使?若存在,求出t的值;若不存在,请说明理由.