山东省聊城市东阿县2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
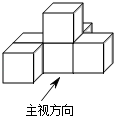
1. 在实数:3.14159, , 1.010 010 001, , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )
 A、主视图 B、左视图 C、俯视图 D、主视图和左视图3. 下列计算正确的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,在中, , 过点A作 , 按下列方式作图:①以点C为圆心,适当长为半径画弧,分别交于点F,G;②分别以点F,G为圆心,大于的长度为半径画弧,两弧交于点H;③作射线交于点E,交于点D,若 . 则的值为( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图3. 下列计算正确的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,在中, , 过点A作 , 按下列方式作图:①以点C为圆心,适当长为半径画弧,分别交于点F,G;②分别以点F,G为圆心,大于的长度为半径画弧,两弧交于点H;③作射线交于点E,交于点D,若 . 则的值为( ) A、 B、 C、 D、6. 在对一组样本数据进行分析时,小华列出了方差的计算公式 , 由公式提供的信息,则该样本的中位数和平均数分别是( )A、2.5,3 B、3,3 C、3,2.5 D、3,47. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( )
A、 B、 C、 D、6. 在对一组样本数据进行分析时,小华列出了方差的计算公式 , 由公式提供的信息,则该样本的中位数和平均数分别是( )A、2.5,3 B、3,3 C、3,2.5 D、3,47. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( ) A、 B、 C、 D、8. 如图,中, , 点B的坐标为 , 将绕点A逆时针旋转得到 , 当点O的对应点C落在上时,点D的坐标为( )
A、 B、 C、 D、8. 如图,中, , 点B的坐标为 , 将绕点A逆时针旋转得到 , 当点O的对应点C落在上时,点D的坐标为( ) A、 B、 C、 D、9. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4 ,则△EFC的周长为( )
A、 B、 C、 D、9. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4 ,则△EFC的周长为( ) A、11 B、10 C、9 D、810. 某货车司机要按计划运输一批零件准点到达指定厂家,他凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,他加快速度仍匀速前进,最后恰好准点送达.如图是该司机行驶的路程与所用时间的函数图象,则该司机原计划准点到达的时刻是( )
A、11 B、10 C、9 D、810. 某货车司机要按计划运输一批零件准点到达指定厂家,他凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,他加快速度仍匀速前进,最后恰好准点送达.如图是该司机行驶的路程与所用时间的函数图象,则该司机原计划准点到达的时刻是( ) A、5:00 B、6:00 C、7:00 D、8:0011. 若关于的方程的解是正数,则的取值范围为( )A、 B、 C、且 D、且12. 如图1,在正方形ABCD中,点F在边BC上,且 , 点E沿BD从点B运动到点D.设点E到边BC的距离为x, , y随x变化的函数图象如图2所示,则图2中函数图象的最低点的坐标为( )
A、5:00 B、6:00 C、7:00 D、8:0011. 若关于的方程的解是正数,则的取值范围为( )A、 B、 C、且 D、且12. 如图1,在正方形ABCD中,点F在边BC上,且 , 点E沿BD从点B运动到点D.设点E到边BC的距离为x, , y随x变化的函数图象如图2所示,则图2中函数图象的最低点的坐标为( )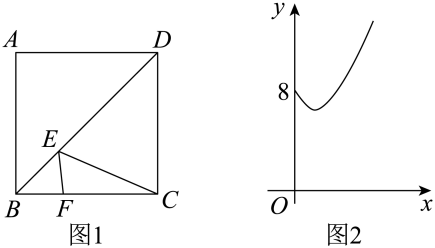 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 将一元二次方程化成(a,b 为常数)的形式,则ab= .14. 如图,已知矩形纸片ABCD, , , 以A为圆心,AD长为半径画弧交BC于点E,将扇形AED剪下围成一个圆锥,则该圆锥的底面半径为 .
 15. 从2名男生和2名女生中任选2名学生参加志愿者服务,那么选出的2名学生中至少有1名女生的概率是.16. 如图,在中, , 点D是边的中点,点P是边上一动点,连接 , 将线段绕点P顺时针旋转,使点D的对应点落在边上,连接 , 若为直角三角形,则的长为 .
15. 从2名男生和2名女生中任选2名学生参加志愿者服务,那么选出的2名学生中至少有1名女生的概率是.16. 如图,在中, , 点D是边的中点,点P是边上一动点,连接 , 将线段绕点P顺时针旋转,使点D的对应点落在边上,连接 , 若为直角三角形,则的长为 . 17. 如图,正方形中, , 与直线l所夹锐角为 , 延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形 , …,依此规律,则线段 .
17. 如图,正方形中, , 与直线l所夹锐角为 , 延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形 , 延长交直线l于点 , 作正方形 , …,依此规律,则线段 .
三、解答题
-
18. 计算:()-1 - 2sin 45°+ |1-|.19. 先化简 , 再求值,其中 .20. 某学校在本校开展了四项“课后服务”项目(项目:足球;项目:篮球;项目:跳绳;项目:书法),要求每名学生必选且只能选修其中一项,为了解学生的选修情况,学校决定进行抽样调查,并根据收集的数据绘制了图1和图2两幅不完整的统计图.
 (1)、本次调查的学生共有人;在扇形统计图中,所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、若全校共有1200名学生, 估计该校选修篮球和跳绳两个项目的总人数.21. 如图,在中, , CD是斜边上的中线, , .
(1)、本次调查的学生共有人;在扇形统计图中,所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、若全校共有1200名学生, 估计该校选修篮球和跳绳两个项目的总人数.21. 如图,在中, , CD是斜边上的中线, , . (1)、求证:四边形BDCE是菱形;(2)、过点E作 , 垂足为点F,若点F是BD的中点, , 求BC的长.22. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具.据了解,只“冰墩墩”和只“雪容融”的进价共计元;只“冰墩墩”和只“雪容融”的进价共计元.(1)、求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.(2)、该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买),求专卖店共有几种采购方案.(3)、若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元,元,则在(2)的条件下,请选出利润最大的采购方案,并求出最大利润.23. 如图,某巡逻艇在海上例行巡逻,上午10时在C处接到海上搜救中心从B处发来的救援任务,此时事故船位于B处的南偏东方向上的A处,巡逻艇位于B处的南偏西方向上1260米处,事故船位于巡逻艇的北偏东方向上,巡逻艇立刻前往A处救援,已知巡逻艇每分钟行驶120米,请估计几分钟可以到达事故船A处.(结果保留整数.参考数据: , , , ).
(1)、求证:四边形BDCE是菱形;(2)、过点E作 , 垂足为点F,若点F是BD的中点, , 求BC的长.22. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具.据了解,只“冰墩墩”和只“雪容融”的进价共计元;只“冰墩墩”和只“雪容融”的进价共计元.(1)、求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.(2)、该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买),求专卖店共有几种采购方案.(3)、若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元,元,则在(2)的条件下,请选出利润最大的采购方案,并求出最大利润.23. 如图,某巡逻艇在海上例行巡逻,上午10时在C处接到海上搜救中心从B处发来的救援任务,此时事故船位于B处的南偏东方向上的A处,巡逻艇位于B处的南偏西方向上1260米处,事故船位于巡逻艇的北偏东方向上,巡逻艇立刻前往A处救援,已知巡逻艇每分钟行驶120米,请估计几分钟可以到达事故船A处.(结果保留整数.参考数据: , , , ). 24. 如图,一次函数的图象与反比例函数的图象交于 , 两点,且一次函数y的图象交x轴于点C,交y轴于点D.
24. 如图,一次函数的图象与反比例函数的图象交于 , 两点,且一次函数y的图象交x轴于点C,交y轴于点D. (1)、求一次函数和反比例函数的解析式;(2)、在第四象限的反比例图象上有一点P,使得 , 请求出点P的坐标:(3)、对于反比例函数 , 当时,直接写出x的取值范围.
(1)、求一次函数和反比例函数的解析式;(2)、在第四象限的反比例图象上有一点P,使得 , 请求出点P的坐标:(3)、对于反比例函数 , 当时,直接写出x的取值范围.