山东省济宁市任城区2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的数是( )A、0 B、-2 C、1 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图所示的几何体是由5个完全相同的小正方体组成,它的主视图是( )
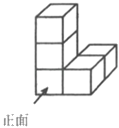 A、
A、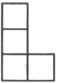 B、
B、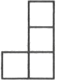 C、
C、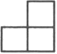 D、
D、 4. 用科学记数法表示202000为( )A、202×1000 B、2.02×105 C、2.02×104 D、(2.02)55. 某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下:67、63、69、55、65,则该组数据的中位数为( )A、63 B、65 C、66 D、696. 函数的自变量x的取值范围是( )A、 B、 C、 D、7. 某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据随意,所列方程正确的是( )A、 B、 C、 D、8. 如图,正六边形 的边长为2,以 为圆心, 的长为半径画弧,得 ,连接 , ,则图中阴影部分的面积为( )
4. 用科学记数法表示202000为( )A、202×1000 B、2.02×105 C、2.02×104 D、(2.02)55. 某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下:67、63、69、55、65,则该组数据的中位数为( )A、63 B、65 C、66 D、696. 函数的自变量x的取值范围是( )A、 B、 C、 D、7. 某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据随意,所列方程正确的是( )A、 B、 C、 D、8. 如图,正六边形 的边长为2,以 为圆心, 的长为半径画弧,得 ,连接 , ,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )
A、 B、 C、 D、9. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )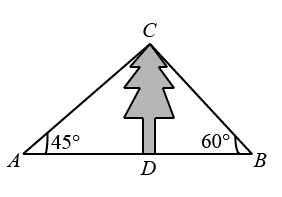 A、 B、 C、 D、10. 生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型来表示.即: , , , , , , 请你推算的个位数字是( )A、 B、 C、 D、
A、 B、 C、 D、10. 生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型来表示.即: , , , , , , 请你推算的个位数字是( )A、 B、 C、 D、二、填空题
-
11. 已知 , , 则的值为.12. 如图, , , , 则的度数为 .
 13. 若关于x的一元二次方程 有两个不相等的实数根,则m的值可以是.(写出一个即可)14. 如图,是的直径,是弦(点C不与点A,点B重合,且点C与点D位于直径AB两侧),若 , 则等于 .
13. 若关于x的一元二次方程 有两个不相等的实数根,则m的值可以是.(写出一个即可)14. 如图,是的直径,是弦(点C不与点A,点B重合,且点C与点D位于直径AB两侧),若 , 则等于 . 15. 将一张以为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 , 其中∠ , 则剪掉的两个直角三角形的斜边长可能是①②③10④其中正确的序号是 .
15. 将一张以为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 , 其中∠ , 则剪掉的两个直角三角形的斜边长可能是①②③10④其中正确的序号是 .
三、解答题
-
16. 计算: .17. 某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每位学生只能参加一个活动小组):A.音乐;B.体育;C.美术;D.阅读;E.人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.

根据图中信息,解答下列问题:
(1)、①此次调查一共随机抽取了 ▲ 名学生;②补全条形统计图(要求在条形图上方注明人数);
③扇形统计图中圆心角 ▲ 度;
(2)、若该校有3200名学生,估计该校参加D组(阅读)的学生人数;(3)、刘老师计划从E组(人工智能)的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.18. 麦收时节,为确保小麦颗粒归仓,某农场安排A,B两种型号的收割机进行小麦收制作业.已知一台A型收割机比一台B型收割机平均每天多收割2公顷小麦,一台A型收割机收割15公顷小麦所用时间与一台B型收割机收割9公顷小麦所用时间相同.(1)、一台A型收割机和一台B型收割机平均每天各收割小麦多少公顷?(2)、该农场安排两种型号的收割机共12台同时进行小麦收割作业,为确保每天完成不少于50公顷的小麦收割任务,至少要安排多少台A型收割机?19. 如图,在平面直角坐标系中,O为坐标原点,点A,B在函数的图象上(点B的横坐标大于点A的横坐标),点A的坐标为 , 过点A作轴于点D,过点B作轴于点C,连接 . (1)、求k的值.(2)、若D为中点,求四边形的面积.20. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,延长BC到点F,使CF=BE,连接DF.
(1)、求k的值.(2)、若D为中点,求四边形的面积.20. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,延长BC到点F,使CF=BE,连接DF.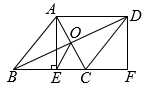 (1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.21. 对于平面直角坐标系中的点M和图形 , 给出如下定义:点P为图形上一点,点Q为图形上一点,当点M是线段PQ的中点时,称点M是图形 , 的“中立点”如果点 , , 那么“中立点”M的坐标为 . 已知,点、 , .
(1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.21. 对于平面直角坐标系中的点M和图形 , 给出如下定义:点P为图形上一点,点Q为图形上一点,当点M是线段PQ的中点时,称点M是图形 , 的“中立点”如果点 , , 那么“中立点”M的坐标为 . 已知,点、 , . (1)、连接 , 在点 , , 中,可以成为点A和线段的“中立点”的是;(2)、已知点 , 的半径为2,如果直线上存在点K可以成为点A和的“中立点”,求点K的坐标;(3)、以点C为圆心,半径为2作圆,点N为直线上的一点,如果存在点N,使得y轴上的一点可以成为点N与的“中立点”,直接写出点N的横坐标n的取值范围.22. 在平面直角坐标系中,已知 , , 且以为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D.
(1)、连接 , 在点 , , 中,可以成为点A和线段的“中立点”的是;(2)、已知点 , 的半径为2,如果直线上存在点K可以成为点A和的“中立点”,求点K的坐标;(3)、以点C为圆心,半径为2作圆,点N为直线上的一点,如果存在点N,使得y轴上的一点可以成为点N与的“中立点”,直接写出点N的横坐标n的取值范围.22. 在平面直角坐标系中,已知 , , 且以为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D. (1)、求点C的坐标和过A,B,C三点的抛物线的析式;(2)、求点D的坐标:(3)、设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
(1)、求点C的坐标和过A,B,C三点的抛物线的析式;(2)、求点D的坐标:(3)、设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.