山东省济宁市梁山县2023年中考一模数学试题

试卷更新日期：2023-05-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 在数轴上，点A表示的数在﹣2的右边，且到﹣2的距离为3，则点A表示的数的倒数为（）

A、﹣1 B、﹣5 C、1 D、﹣ $\frac{1}{5}$

查看试题解析
2. 下列各式计算正确的是（）

A、 $(x + y)^{2} = x^{2} + y^{2}$ B、 ${(x^{2})}^{3} = x^{5}$ C、 $x^{2} \cdot x^{3} = x^{5}$ D、 $4 x^{2} - y^{2} = (4 x + y) (4 x - y)$

查看试题解析
3. 中秋节上，同学设计了如图的艺术字“中秋快乐”，下面展示如图几何体“中”字的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = \sqrt{3} A C$ ，将 $R t △ A B C$ 绕点 $A$ 逆时针旋转 $45 °$ 后，到 $R t △ A E D$ ，点 $B$ 经过的路径为弧 $B E$ ，已知 $A C = 2$ ，则图中阴影部分的面积为（）．

A、π B、 $\sqrt{3}$ π C、 $2$ π D、 $3$ π

查看试题解析
5. 不等式组 ${\begin{array}{l} 3 x + 1 \geq 7 \\ 4 x - 3 < 9 \end{array}$ 的解集是（）

A、 $x \geq 2$ B、 $x < 3$ C、 $x < \frac{3}{2}$ D、 $2 \leq x < 3$

查看试题解析
6. 对于实数 a，b，定义运算“#”如下：a#b＝a²－ab，如：3#2＝3²－3×2＝3，则方程（x＋1）#3＝2的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
7. 五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元．追加后的5个数据与之前的5个数据相比，集中趋势相同的是（）

A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数

查看试题解析
8. 估计 $(2 \sqrt{2} + \sqrt{3}) \times \sqrt{2}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
9. 如图，四边形ABCD内接于⊙O，F是 $\hat{C D}$ 上一点，且 $\hat{D F}$ = $\hat{B C}$ ，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC=105°，∠BAC=25°，则∠E的度数为（）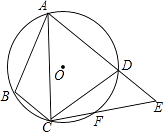

A、45° B、50° C、55° D、60°

查看试题解析
10. 如图，在平面直角坐标系中，点 $A_{1}$ 在 $x$ 轴的正半轴上， $B_{1}$ 在第一象限，且△ $O A_{1} B_{1}$ 是等边三角形.在射线 $O B_{1}$ 上取点 $B_{2}$ ， $B_{3}$ ， $\dots$ ，分别以 $B_{1} B_{2}$ ， $B_{2} B_{3}$ ， $\dots$ 为边作等边三角形△ $B_{1} A_{2} B_{2}$ ， △ $B_{2} A_{3} B_{3}$ ， $\dots$ 使得 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $\dots$ 在同一直线上，该直线交 $y$ 轴于点 $C$ .若 $O A_{1} = 1$ ， $∠ O A_{1} C = 30 °$ ，则点 $B_{9}$ 的横坐标是（）

A、 $\frac{255}{2}$ B、 $\frac{511}{2}$ C、256 D、 $\frac{513}{2}$

查看试题解析

二、填空题

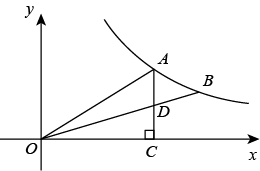
11. 这段时间，一个叫“学习强国”的理论学习平台火了，很多人主动下载、积分打卡，兴起了一股全民学习的热潮.据不完全统计，截止4月2号，华为官方应用市场“学习强国APP”下载量已达8830万次，请将8830万用科学记数法表示为是.

查看试题解析
12. 如果式子 $\frac{\sqrt{1 - x}}{x + 2}$ 有意义，那么x的取值范围是．

查看试题解析
13. 如图，A，B是双曲线y＝ $\frac{k}{x}$ （x＞0）上的两点，连接OA，OB．过点A作AC⊥x轴于点C，交OB于点D．若D为AC的中点，△AOD的面积为3，点B的坐标为（m，2），则m的值为．

查看试题解析
14. “孔子周游列国”是流传很广的故事．有一次他和学生到离他们住的驿站30里的书院参观，学生步行出发1小时后，孔子坐牛车出发，牛车的速度是步行的1.5倍，孔子和学生们同时到达书院，设学生步行的速度为每小时x里，则可列方程为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C + ∠ A C B = 130 °$ ，按图进行翻折，使 $M D ∥ N G ∥ B C$ ， $M E ∥ F G$ ，则 $∠ N F E$ 的度数是 $°$ ．

查看试题解析

三、解答题

16. 分式化简： $(\frac{2 a - 1}{a + 1} - a + 1) \div \frac{a^{2} - 4 a + 4}{a + 1} + 1$ .

查看试题解析
17. 梁山县某学校在落实“双减”的背景下，决定在课后延时服务中组织学生开展社团活动，现准备开设手工、摄影、航模，编程四门校本课程，规定每名学生必须且只能选修一门校本课程，学校对七年级学生选修校本课程的情况进行了抽样调查，根据调查结果绘制了下面两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题．

(1)、补全条形统计图和扇形统计图；

(2)、若本次调查中选择“航模”课程中的女生占 $20 %$ ，则在全校 $2800$ 名学生中，请你估计约有多少名女生会选择“航模”课程；

(3)、将2名选修“航模”的学生和2名选修“编程”的学生编为一组，再从中随机抽取2人，请用画树状图的方法求出2人都选修“航模”的概率．

查看试题解析
18. 如图，已知 $∠ A O B$ ，点 $M$ 为 $O B$ 上一点．

(1)、画 $M C ⊥ O A$ ，垂足为 $C$ ；

(2)、画 $∠ A O B$ 的平分线，交 $M C$ 于 $D$ ．（注：不需要写出作法，只需保留作图痕迹）

查看试题解析
19. 某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润 $y_{1}$ 与投资量x成正比例关系，如图1所示；种植花卉的利润 $y_{2}$ 与投资量x成二次函数关系，如图2所示（注：利润与投资量的单位都是万元）．

(1)、直接写出利润 $y_{1}$ 与 $y_{2}$ 关于投资量x的函数关系式；

(2)、如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？

查看试题解析
20. 如图，线段 $A B$ 是 $⊙ O$ 的直径， $⊙ O$ 交线段 $B C$ 于D，且D是 $B C$ 的中点， $D E ⊥ A C$ 于E，连接 $A D$ .

(1)、求证： $D E$ 是 $⊙ O$ 的切线.

(2)、若 $A E = 1$ ， $A B = 4$ ，求 $A D$ 的长.

查看试题解析
21. 如果一元二次方程的两根相差1，那么该方程称为“差1方程”．例如 $x^{2} + x = 0$ 是“差1方程”．

(1)、判断下列方程 $x^{2} - 5 x - 6 = 0$ 是否为“差1方程”？

(2)、已知关于x的方程 $x^{2} - (m - 1) x - m = 0$ （m是常数）是“差1方程”，求m的值；

(3)、若关于x的方程 $a x^{2} + b x + 1 = 0$ （ $a ， b$ 是常数， $a > 0$ ）是“差1方程”，设 $t = 10 a - b^{2}$ ，求t的最大值．

查看试题解析