山东省济宁市金乡县2023年中考二模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 中国2023年2月份重要宏观经济数据先后已公布,其中1—2月份发电量约为13500亿千瓦时,同比增长0.7%,13500亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算,正确的是( )A、 B、 C、 D、4. 某树主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支总数是43.若设主干长出x个支干,则可列方程为( )A、 B、 C、 D、5. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )
2. 中国2023年2月份重要宏观经济数据先后已公布,其中1—2月份发电量约为13500亿千瓦时,同比增长0.7%,13500亿用科学记数法表示为( )A、 B、 C、 D、3. 下列计算,正确的是( )A、 B、 C、 D、4. 某树主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支总数是43.若设主干长出x个支干,则可列方程为( )A、 B、 C、 D、5. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )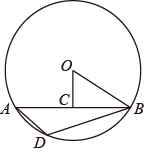 A、 B、 C、 D、6. 如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.则斜坡CD的长度为( ).
A、 B、 C、 D、6. 如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.则斜坡CD的长度为( ). A、 B、 C、 D、7. 如图,点A,B的坐标分别为和 , 抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为 , 则点D的横坐标最大值为( )
A、 B、 C、 D、7. 如图,点A,B的坐标分别为和 , 抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为 , 则点D的横坐标最大值为( ) A、 B、1 C、5 D、88. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )
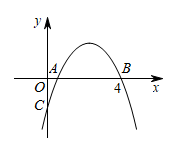
A、 B、1 C、5 D、88. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )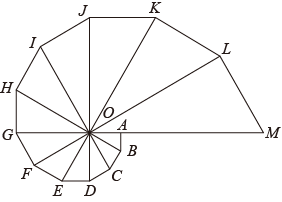 A、()3 B、()7 C、()6 D、()69. 如图,抛物线与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 , 则下列结论中,正确的个数是( )
A、()3 B、()7 C、()6 D、()69. 如图,抛物线与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 , 则下列结论中,正确的个数是( )①;
②;
③与是抛物线上两点,若 , 则;
④若抛物线的对称轴是直线 , m为任意实数,则;
 A、1个 B、2个 C、3个 D、4个10. 如图,在正方形ABCD中,点G是BC上一点,且 ,连接DG交对角线AC于F点,过D点作DE⊥DG交CA的延长线于点E,若AE=3,则DF的长为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在正方形ABCD中,点G是BC上一点,且 ,连接DG交对角线AC于F点,过D点作DE⊥DG交CA的延长线于点E,若AE=3,则DF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果代数式 有意义,那么字母x的取值范围是 .12. 一副三角板如图放置, , , , 则 .
 13. 已知圆锥的侧面展开图的面积是 ,圆心角是60°,则这个圆锥的底面圆的半径是 .14. 如图,在中, , , , 为上的一动点,于 , 于 , 为的中点,则的最小值为 .
13. 已知圆锥的侧面展开图的面积是 ,圆心角是60°,则这个圆锥的底面圆的半径是 .14. 如图,在中, , , , 为上的一动点,于 , 于 , 为的中点,则的最小值为 .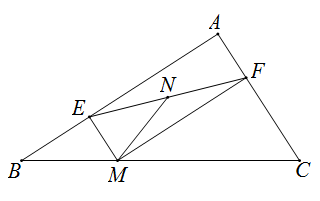 15. 如图,一次函数的图像与x轴和y轴分别交于点A和点B与反比例函数上的图像在第一象限内交于点C,轴,轴,垂足分别为点D,E,当时,k的值为 .
15. 如图,一次函数的图像与x轴和y轴分别交于点A和点B与反比例函数上的图像在第一象限内交于点C,轴,轴,垂足分别为点D,E,当时,k的值为 .
三、解答题
-
16. 计算:;17. 为落实重庆市关于开展中小学课后服务工作的要求,某学校开展了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.全校共有100名学生选择了A课程,为了解选A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试.将他们的成绩(百分制)绘制成频数分布直方图.
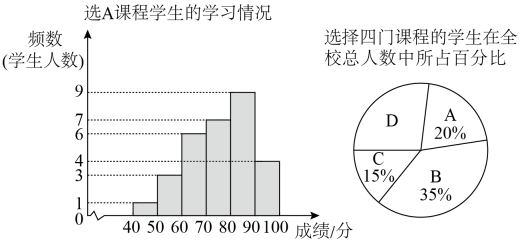 (1)、其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是 , 众数是 .(2)、根据题中信息,估计该校共有人,选A课程学生成绩在80≤x<90的有人.(3)、课程D在扇形统计图中所对应的圆心角的度数为 .(4)、如果学校规定每名学生要选两门不同的课程,小张和小王在选课程中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明.18. 如图,直线y=kx+b与双曲线y=相交于A(1,2),B两点,与x轴相交于点C(4,0).
(1)、其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是 , 众数是 .(2)、根据题中信息,估计该校共有人,选A课程学生成绩在80≤x<90的有人.(3)、课程D在扇形统计图中所对应的圆心角的度数为 .(4)、如果学校规定每名学生要选两门不同的课程,小张和小王在选课程中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明.18. 如图,直线y=kx+b与双曲线y=相交于A(1,2),B两点,与x轴相交于点C(4,0). (1)、分别求直线AC和双曲线对应的函数表达式;(2)、连接OA,OB,求△AOB的面积;(3)、直接写出当x>0时,关于x的不等式kx+b>的解集.19. 为助力苏州市双碳目标实现,充分挖掘学校光伏发电资源,学校屋顶安装了太阳能电板. 图①是太阳能电板的实物图,其截面示意图如图②,为太阳能电板,其一端固定在水平面上且夹角 , 另一端与支撑钢架相连,钢架底座和水平面垂直,且. 若 , , 求的长. (参考数据: , 结果精确到. )
(1)、分别求直线AC和双曲线对应的函数表达式;(2)、连接OA,OB,求△AOB的面积;(3)、直接写出当x>0时,关于x的不等式kx+b>的解集.19. 为助力苏州市双碳目标实现,充分挖掘学校光伏发电资源,学校屋顶安装了太阳能电板. 图①是太阳能电板的实物图,其截面示意图如图②,为太阳能电板,其一端固定在水平面上且夹角 , 另一端与支撑钢架相连,钢架底座和水平面垂直,且. 若 , , 求的长. (参考数据: , 结果精确到. ) 20. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?21. 如图,在 中, ,以 为直径的 交 于点D,连接 ,过点D作 ,垂足为M, 、 的延长线交于点N.
20. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?21. 如图,在 中, ,以 为直径的 交 于点D,连接 ,过点D作 ,垂足为M, 、 的延长线交于点N. (1)、求证: 是 的切线;(2)、求证 ;(3)、若 ,求 的直径.22. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
(1)、求证: 是 的切线;(2)、求证 ;(3)、若 ,求 的直径.22. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.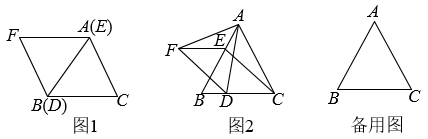 (1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.
(1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.