山东省济南市2023年中考二模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 如图所示三视图的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 的相反数为A、 B、3 C、 D、3. 地球绕太阳转动一天通过的路程约是2640000千米,用科学记数法表示为( )A、2.64×107 B、2.64×106 C、26.4×105 D、264×1044. 加强生活垃圾管理,维护公共环境和节约资源是全社会公共的责任.我市将全面推行生活垃圾强制分类.下列四个垃圾分类标识中的图形是轴对称图形的是( )A、
2. 的相反数为A、 B、3 C、 D、3. 地球绕太阳转动一天通过的路程约是2640000千米,用科学记数法表示为( )A、2.64×107 B、2.64×106 C、26.4×105 D、264×1044. 加强生活垃圾管理,维护公共环境和节约资源是全社会公共的责任.我市将全面推行生活垃圾强制分类.下列四个垃圾分类标识中的图形是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 已知实数a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )
5. 已知实数a,b在数轴上的对应点的位置如图所示,下列结论正确的是( ) A、a﹣b>0 B、a+b>0 C、ab>0 D、|a+1|<|b+1|6. 如图, ∥ , 为直线 上两点,且 平分 ;若 ,则∠2的度数为( )
A、a﹣b>0 B、a+b>0 C、ab>0 D、|a+1|<|b+1|6. 如图, ∥ , 为直线 上两点,且 平分 ;若 ,则∠2的度数为( )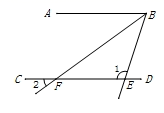 A、30° B、36° C、42° D、45°7. 如图,电路图上有四个开关 , , , 和一个小灯泡,闭合开关或同时闭合开关 , , 都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A、30° B、36° C、42° D、45°7. 如图,电路图上有四个开关 , , , 和一个小灯泡,闭合开关或同时闭合开关 , , 都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( ) A、 B、 C、 D、8. 某大桥采用了低塔斜拉桥桥型(如图1),图2是从图1抽象出的平面图,假设站在桥上测得拉索与水平桥面的夹角是30°,拉索的坡度(或坡比) , 两拉索底端距离是18米,则立柱的高度是( )
A、 B、 C、 D、8. 某大桥采用了低塔斜拉桥桥型(如图1),图2是从图1抽象出的平面图,假设站在桥上测得拉索与水平桥面的夹角是30°,拉索的坡度(或坡比) , 两拉索底端距离是18米,则立柱的高度是( ) A、18米 B、米 C、米 D、9米9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( )
A、18米 B、米 C、米 D、9米9. 如图,在 中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4, 面积为10,则BM+MD长度的最小值为( ) A、 B、3 C、4 D、510. 规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧), , 线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )A、 B、 C、或 D、或
A、 B、3 C、4 D、510. 规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧), , 线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )A、 B、 C、或 D、或二、填空题
-
11. 在实数范围内分解因式: .12. 在卡塔尔世界杯上,来自中国制造的主体育场馆“大金碗”——卢塞尔体育场(图①),融合了许多黑科技,球场顶棚采用环保膜材料,既可以为观众提供遮阳,又能够给球场草地带来阳光.膜的材料结构是由许多正六边形交织而成的,正六边形(图②)中,为°.
 13. 某学习小组在“世界读书日”这天统计了本组5名同学在上学期阅读课外书籍的册数,数据是18,x,15,16,13,若这组数据的平均数为16,则这组数据的中位数是 .14. 分式方程的解为x= .15. 如图,正方形的顶点 分别在 轴和 轴上,边 的中点 在 轴上,若反比例函数 的图象恰好经过 的中点 ,则 的长为 .
13. 某学习小组在“世界读书日”这天统计了本组5名同学在上学期阅读课外书籍的册数,数据是18,x,15,16,13,若这组数据的平均数为16,则这组数据的中位数是 .14. 分式方程的解为x= .15. 如图,正方形的顶点 分别在 轴和 轴上,边 的中点 在 轴上,若反比例函数 的图象恰好经过 的中点 ,则 的长为 . 16. 如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在 处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点 处,EF为折痕,连接 .若CF=3,则tan =.
16. 如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在 处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点 处,EF为折痕,连接 .若CF=3,则tan =.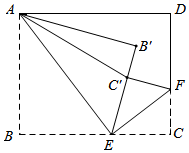
三、解答题
-
17. 计算: .18. 解不等式组: , 并写出的所有整数解.19. 已知:如图,在平行四边形中, , 是对角线上两点,连接 , , 求证: .
 20. 某校政治实践小组就近期人们比较关注的五个话题:“A.5G通讯;B.民法典;C.北斗导航;D.数字经济;E . 小康社会”,对学生进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.
20. 某校政治实践小组就近期人们比较关注的五个话题:“A.5G通讯;B.民法典;C.北斗导航;D.数字经济;E . 小康社会”,对学生进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
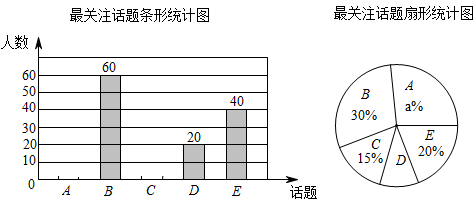 (1)、政治实践小组在这次活动中,调查的学生共有人;(2)、将图中的最关注话题条形统计图补充完整;(3)、政治实践小组进行专题讨论中,甲、乙两个小组从三个话题:“A.5G通讯;B.民法典;C.北斗导航”中抽签(不放回)选一项进行发言,利用树状图或表格,求出两个小组选择A、B话题发言的概率.21. 如图,在数学综合实践活动课上,两名同学要测量小河对岸大树BC的高度,甲同学在点A测得大树顶端B的仰角为45°,乙同学从A点出发沿斜坡走6米到达斜坡上点D,在此处测得树顶端点B的仰角为26.7°,且斜坡AF的坡度为1:2.
(1)、政治实践小组在这次活动中,调查的学生共有人;(2)、将图中的最关注话题条形统计图补充完整;(3)、政治实践小组进行专题讨论中,甲、乙两个小组从三个话题:“A.5G通讯;B.民法典;C.北斗导航”中抽签(不放回)选一项进行发言,利用树状图或表格,求出两个小组选择A、B话题发言的概率.21. 如图,在数学综合实践活动课上,两名同学要测量小河对岸大树BC的高度,甲同学在点A测得大树顶端B的仰角为45°,乙同学从A点出发沿斜坡走6米到达斜坡上点D,在此处测得树顶端点B的仰角为26.7°,且斜坡AF的坡度为1:2. (1)、求乙同学从点A到点D的过程中上升的高度;(2)、依据他们测量的数据求出大树BC的高度.(参考数据:sin26.7°≈0.45,cos26.7°≈0.89,tan26.7°≈0.50)22. 如图,AB为⊙O的直径,点C是⊙O上一点,CD与⊙O相切于点C,过点A作AD⊥DC,连接AC,BC.
(1)、求乙同学从点A到点D的过程中上升的高度;(2)、依据他们测量的数据求出大树BC的高度.(参考数据:sin26.7°≈0.45,cos26.7°≈0.89,tan26.7°≈0.50)22. 如图,AB为⊙O的直径,点C是⊙O上一点,CD与⊙O相切于点C,过点A作AD⊥DC,连接AC,BC.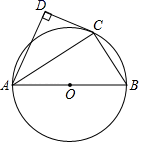 (1)、求证:AC是∠DAB的角平分线;(2)、若AD=2,AB=3,求AC的长.23. 一文具厂接到生产一批橡皮和水笔的任务,已知该文具厂销售200个橡皮和200个水笔的利润为160元,销售100个橡皮和200个水笔的利润为130元.已知该文具厂每天生产橡皮和水笔共4500个,生产橡皮和水笔每个成本分别为2元,3元,设每天生产橡皮个,该文具厂每天生产成本为元.(1)、求橡皮和水笔的销售单价;(2)、求关于的函数关系式;(3)、若该文具厂每天最多投入成本为10000元,求该文具厂每天获得利润最多是多少元?24. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B.
(1)、求证:AC是∠DAB的角平分线;(2)、若AD=2,AB=3,求AC的长.23. 一文具厂接到生产一批橡皮和水笔的任务,已知该文具厂销售200个橡皮和200个水笔的利润为160元,销售100个橡皮和200个水笔的利润为130元.已知该文具厂每天生产橡皮和水笔共4500个,生产橡皮和水笔每个成本分别为2元,3元,设每天生产橡皮个,该文具厂每天生产成本为元.(1)、求橡皮和水笔的销售单价;(2)、求关于的函数关系式;(3)、若该文具厂每天最多投入成本为10000元,求该文具厂每天获得利润最多是多少元?24. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B.
 (1)、求a,k的值;(2)、直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
(1)、求a,k的值;(2)、直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;
②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
25. 在 中, , ,点 在边 上, ,将线段 绕点 顺时针旋转至 ,记旋转角为 ,连接 , ,以 为斜边在其一侧制作等腰直角三角形 .连接 .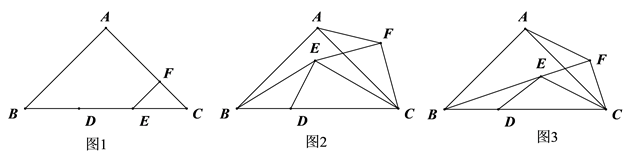 (1)、如图1,当 时,请直接写出线段 与线段 的数量关系;(2)、当 时,
(1)、如图1,当 时,请直接写出线段 与线段 的数量关系;(2)、当 时,①如图2,(1)中线段 与线段 的数量关系是否仍然成立?请说明理由;
②如图3,当 , , 三点共线时,连接 ,判断四边形 的形状,并说明理由.
26. 如图.已知抛物线经过三点,点P为直线上方抛物线上一点. (1)、求抛物线的解析式;(2)、当时,求点P的坐标;(3)、连接 , 交直线于点E,交y轴于点F;
(1)、求抛物线的解析式;(2)、当时,求点P的坐标;(3)、连接 , 交直线于点E,交y轴于点F;①是否存在点P使与相似,若存在,求出点P的坐标,若不存在,请说明理由;
②若点P的坐标为 , 点H在抛物线上,过H作轴,交直线于点K.点Q是平面内一点,当以点E,H,K,Q为顶点的四边形是正方形时,请直接写出点Q的坐标.