山东省济南市章丘区2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 国家卫健委通报:截至2021年6月19日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗101000万余剂次,建立免疫屏障,我们一起努力!将数字101000用科学记数法表示为( )A、 B、 C、 D、3. 如图,直线 , 直角三角板的直角顶点落在直线b上.若 , 则等于( )
 A、 B、 C、 D、4. 化简的结果是A、 B、 C、 D、5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、 B、 C、 D、4. 化简的结果是A、 B、 C、 D、5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 函数与在同一坐标系内的图象可能是( )A、
6. 下列运算正确的是( )A、 B、 C、 D、7. 函数与在同一坐标系内的图象可能是( )A、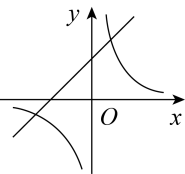 B、
B、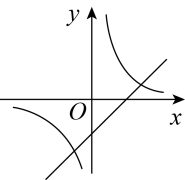 C、
C、 D、
D、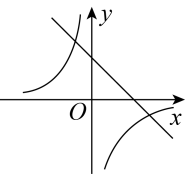 8. 如图,在平面直角坐标系中,的顶点都在方格线的格点上,将绕点A逆时针方向旋转 , 得到 , 则点C的对应点的坐标为( )
8. 如图,在平面直角坐标系中,的顶点都在方格线的格点上,将绕点A逆时针方向旋转 , 得到 , 则点C的对应点的坐标为( ) A、 B、 C、 D、9. 如图,在中,以点A为圆心,以适当长为半径作弧,分别交 , 于点E,F,再分别以E、F为圆心,以相同长度为半径作弧,两弧相交于点O,P为射线上任意一点,过点P作 , 交于点M,连接 , 若 , , 则长度的最小值为( )
A、 B、 C、 D、9. 如图,在中,以点A为圆心,以适当长为半径作弧,分别交 , 于点E,F,再分别以E、F为圆心,以相同长度为半径作弧,两弧相交于点O,P为射线上任意一点,过点P作 , 交于点M,连接 , 若 , , 则长度的最小值为( )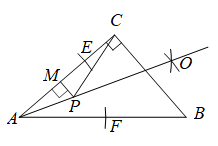 A、 B、 C、4 D、10. 在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为雅系点.已知二次函数的图象上有且只有一个雅系点 , 且当时,函数的最小值为 , 最大值为 , 则m的取值范围是( )A、 B、 C、 D、
A、 B、 C、4 D、10. 在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为雅系点.已知二次函数的图象上有且只有一个雅系点 , 且当时,函数的最小值为 , 最大值为 , 则m的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 .
 13. 如图,飞镖游戏板由大小相等的小正方形格子构成,小东向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
13. 如图,飞镖游戏板由大小相等的小正方形格子构成,小东向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 . 14. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动,如图折线和线段分别表示小泽和小帅离甲地的距离(单位:千米)与时间x(单位:小时)之间函数关系的图象,则当小帅到达乙地时,小泽距甲地的距离为千米.
14. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动,如图折线和线段分别表示小泽和小帅离甲地的距离(单位:千米)与时间x(单位:小时)之间函数关系的图象,则当小帅到达乙地时,小泽距甲地的距离为千米. 15. 如图.将扇形翻折,使点与圆心重合,展开后折痕所在直线与交于点 , 连接 . 若 , 则图中阴影部分的面积是 .
15. 如图.将扇形翻折,使点与圆心重合,展开后折痕所在直线与交于点 , 连接 . 若 , 则图中阴影部分的面积是 . 16. 如图,在矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连接EF.已知AB=6,BC=8,则EF的长为 .
16. 如图,在矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连接EF.已知AB=6,BC=8,则EF的长为 .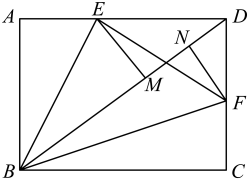
三、解答题
-
17. 计算:18. 解不等式组: , 并写出它的所有整数解.19. 如图,在菱形ABCD中,M,N分别是AB和BC上的点,且AM=CN,求证:∠DMN=∠DNM.
 20. 图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角为 , 长为3米的真空管AB与水平线AD的夹角为 , 安装热水器的铁架竖直管CE的长度为0.5米.
20. 图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角为 , 长为3米的真空管AB与水平线AD的夹角为 , 安装热水器的铁架竖直管CE的长度为0.5米. (1)、真空管上端B到水平线AD的距离.(2)、求安装热水器的铁架水平横管BC的长度.(结果精确到0.1米)
(1)、真空管上端B到水平线AD的距离.(2)、求安装热水器的铁架水平横管BC的长度.(结果精确到0.1米)参考数据: , , , , ,
21. 为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.(1)、求A,B两种学习用品的单价各是多少元;(2)、若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?22. 如图,AB是⊙O的直径,C为⊙O上一点,过点O作OD⊥AB,交AC的延长线于点D,交过点C的切线于点 E.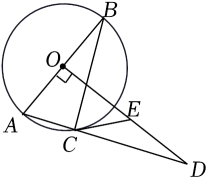 (1)、求证:∠DCE=∠ABC;(2)、若OA=3,AC=2,求线段CD的长.23. 我市各学校积极响应上级“停课不停教、停课不停学”的要求,开展了空中在线教学.某校就“网络直播课”的满意度进行了随机在线问卷调查,调查结果分为四类:A.非常满意;B.很满意;C.一般;D.不满意.将收集到的信息进行了统计,绘制成不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题.
(1)、求证:∠DCE=∠ABC;(2)、若OA=3,AC=2,求线段CD的长.23. 我市各学校积极响应上级“停课不停教、停课不停学”的要求,开展了空中在线教学.某校就“网络直播课”的满意度进行了随机在线问卷调查,调查结果分为四类:A.非常满意;B.很满意;C.一般;D.不满意.将收集到的信息进行了统计,绘制成不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题.频数分布统计表
类别
频数
频率
A
60
h
B
m
0.4
C
90
0.3
D
30
0.1
 (1)、接受问卷调查的学生共有人; ,(2)、补全条形统计图:(3)、为改进教学,学校决定从选填结果是D类的学生中,选取甲、乙、丙、丁四人,随机抽取两名学生参与网络座谈会,用画树状图或列表的方法,求甲、乙两名同学同时被抽中的概率.24. 如图,在平面直角坐标系中,直线与反比例函数的图象交于点 , 与轴交于点 , 点是反比例函数的图象上一动点,过点作直线轴交直线于点 , 设点的横坐标为 , 且 , 连接 , .
(1)、接受问卷调查的学生共有人; ,(2)、补全条形统计图:(3)、为改进教学,学校决定从选填结果是D类的学生中,选取甲、乙、丙、丁四人,随机抽取两名学生参与网络座谈会,用画树状图或列表的方法,求甲、乙两名同学同时被抽中的概率.24. 如图,在平面直角坐标系中,直线与反比例函数的图象交于点 , 与轴交于点 , 点是反比例函数的图象上一动点,过点作直线轴交直线于点 , 设点的横坐标为 , 且 , 连接 , . (1)、求 , 的值.(2)、当的面积为3时,求点的坐标.(3)、设的中点为 , 点为轴上一点,点为坐标平面内一点,当以 , , , 为顶点的四边形为正方形时,求出点的坐标.25. 在中, , , 点D在BC上,且满足 , 将线段DB绕点D顺时针旋转至DE,连接CE,BE,以CE为斜边在其右侧作直角三角形CEF,且 , , 连接AF.
(1)、求 , 的值.(2)、当的面积为3时,求点的坐标.(3)、设的中点为 , 点为轴上一点,点为坐标平面内一点,当以 , , , 为顶点的四边形为正方形时,求出点的坐标.25. 在中, , , 点D在BC上,且满足 , 将线段DB绕点D顺时针旋转至DE,连接CE,BE,以CE为斜边在其右侧作直角三角形CEF,且 , , 连接AF. (1)、如图1,当点E落在BC上时,直接写出线段BE与线段AF的数量关系;(2)、如图2,在线段DB旋转过程中,(1)中线段BE与线段AF的数量关系是否仍然成立?请利用图2说明理由;(3)、如图3,连接DF,若 , 求线段DF长度的最小值.26. 如图,抛物线与x轴交于 , B两点,与y轴交于点C , 连接 .
(1)、如图1,当点E落在BC上时,直接写出线段BE与线段AF的数量关系;(2)、如图2,在线段DB旋转过程中,(1)中线段BE与线段AF的数量关系是否仍然成立?请利用图2说明理由;(3)、如图3,连接DF,若 , 求线段DF长度的最小值.26. 如图,抛物线与x轴交于 , B两点,与y轴交于点C , 连接 . (1)、求抛物线的解析式.(2)、点P是第三象限抛物线上一点,直线与y轴交于点D,的面积为12,求点P的坐标.(3)、抛物线上是否存在点Q使得?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式.(2)、点P是第三象限抛物线上一点,直线与y轴交于点D,的面积为12,求点P的坐标.(3)、抛物线上是否存在点Q使得?若存在,请求出点Q的坐标;若不存在,请说明理由.