山东省济南市商河县2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 如图是由6个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )
 A、
A、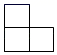 B、
B、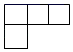 C、
C、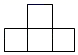 D、
D、 3. 为增强市民节水意识,近日,我县组织开展“一滴水,一世界”节水主题宣传活动,约26000人参与,这里的26000科学记数法表示为( )A、 B、 C、 D、4. 如图,∠1+∠2等于( )
3. 为增强市民节水意识,近日,我县组织开展“一滴水,一世界”节水主题宣传活动,约26000人参与,这里的26000科学记数法表示为( )A、 B、 C、 D、4. 如图,∠1+∠2等于( ) A、60° B、90° C、110° D、180°5. 下列图形中,是中心对称图形的是( )A、
A、60° B、90° C、110° D、180°5. 下列图形中,是中心对称图形的是( )A、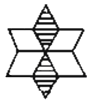 B、
B、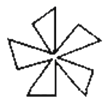 C、
C、 D、
D、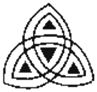 6. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、7. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3).则顶点C的坐标为( )
6. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、7. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3).则顶点C的坐标为( )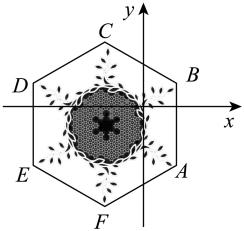 A、 B、 C、 D、8. 某中学为了创建“最美校园图书屋”新购买了一批图书,其中科普类图书平均每本书的价格是文学类书平均每本书价格的1.2倍,已知学校用1200元购买文学类图书的本数比用这些钱购买科普类图书的本数多10本,设文学类图书平均每本书的价格是x元,则下列方程正确的是( )A、 B、 C、 D、9. 如图,在菱形中,分别以为圆心,大于长为半径作弧,两弧分别交于点 , 连接 , 若直线恰好经过点 , 与边交于点 , 连接 . 有以下四个结论:① , ②如果 , 那么 , ③ , ④;其中正确结论的个数是( )
A、 B、 C、 D、8. 某中学为了创建“最美校园图书屋”新购买了一批图书,其中科普类图书平均每本书的价格是文学类书平均每本书价格的1.2倍,已知学校用1200元购买文学类图书的本数比用这些钱购买科普类图书的本数多10本,设文学类图书平均每本书的价格是x元,则下列方程正确的是( )A、 B、 C、 D、9. 如图,在菱形中,分别以为圆心,大于长为半径作弧,两弧分别交于点 , 连接 , 若直线恰好经过点 , 与边交于点 , 连接 . 有以下四个结论:① , ②如果 , 那么 , ③ , ④;其中正确结论的个数是( ) A、个 B、个 C、个 D、个10. 已知二次函数的表达式为 , 将其图象向右平移个单位,得到二次函数的图象,使得当时,随x增大而增大;当时,随x增大而减小.则实数k的取值范围是( )A、 B、 C、 D、
A、个 B、个 C、个 D、个10. 已知二次函数的表达式为 , 将其图象向右平移个单位,得到二次函数的图象,使得当时,随x增大而增大;当时,随x增大而减小.则实数k的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 分解因式: =.
12. 小华在如图所示的4×4正方形网格纸板上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是 . 13. 函数y= 中,自变量x的取值范围是 .14. 若关于x的一元二次方程有一个根为0,则a的值等于 .15. 对数的定义:一般地,若(且),那么叫做以为底的对数,记作 , 比如指数式可以转化为对数式 , 对数式 , 可以转化为指数式 . 计算 .16. 正方形中, , E为AB的中点,将沿折叠得到 , , 垂足为 , 则.
13. 函数y= 中,自变量x的取值范围是 .14. 若关于x的一元二次方程有一个根为0,则a的值等于 .15. 对数的定义:一般地,若(且),那么叫做以为底的对数,记作 , 比如指数式可以转化为对数式 , 对数式 , 可以转化为指数式 . 计算 .16. 正方形中, , E为AB的中点,将沿折叠得到 , , 垂足为 , 则.
三、解答题
-
17. 计算: .18. 解不等式组: , 并写出它的所有整数解.19. 如图,在▱ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.
求证:BC=BF.
 20. 某校为了了解家长和学生的参与“防疫教育”的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;C.仅家长自己参与;D.家长和学生都未参与,请根据图中提供的信息,解答下列问题:
20. 某校为了了解家长和学生的参与“防疫教育”的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;C.仅家长自己参与;D.家长和学生都未参与,请根据图中提供的信息,解答下列问题: (1)、在这次抽样调查中,共调查了名学生?(2)、补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数 ▲ ;(3)、根据抽样调查结果,估计该校名学生中“家长和学生都参与”的人数.21. 图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为 , 主臂长为 , 测得主臂伸展角 .
(1)、在这次抽样调查中,共调查了名学生?(2)、补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数 ▲ ;(3)、根据抽样调查结果,估计该校名学生中“家长和学生都参与”的人数.21. 图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为 , 主臂长为 , 测得主臂伸展角 .(参考数据:)
 (1)、求点P到地面的高度;(2)、若挖掘机能挖的最远处点Q到点N的距离为 , 求的度数.22. 如图,在中, , 点F在上,以为直径的恰好经过点E,且边与切于点E,连接 .
(1)、求点P到地面的高度;(2)、若挖掘机能挖的最远处点Q到点N的距离为 , 求的度数.22. 如图,在中, , 点F在上,以为直径的恰好经过点E,且边与切于点E,连接 . (1)、求证:平分;(2)、若 , 求的长.23. 我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.(1)、求甲、乙两种奖品的单价;(2)、根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的 , 应如何购买才能使总费用最少?并求出最少费用。24. 已知直线与反比例函数的图象在第一象限交于点.
(1)、求证:平分;(2)、若 , 求的长.23. 我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.(1)、求甲、乙两种奖品的单价;(2)、根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的 , 应如何购买才能使总费用最少?并求出最少费用。24. 已知直线与反比例函数的图象在第一象限交于点.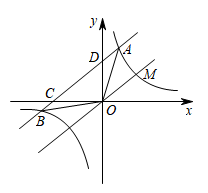 (1)、求反比例函数的解析式;(2)、如图,将直线向上平移个单位后与的图象交于点和点 , 求的值;(3)、在(2)的条件下,设直线与轴、轴分别交于点 , , 求证:.25. 如图,四边形、都是正方形.
(1)、求反比例函数的解析式;(2)、如图,将直线向上平移个单位后与的图象交于点和点 , 求的值;(3)、在(2)的条件下,设直线与轴、轴分别交于点 , , 求证:.25. 如图,四边形、都是正方形. (1)、如图1,若 , , 求的长;(2)、如图2,正方形绕点B逆时针旋转,使点G正好落在上,求证:;(3)、如图3,在(2)条件下, , , 点M为直线上一动点,连接 , 过点作 , 垂足为点 , 直接写出的最小值为 .26. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线经过两点,与x轴的另一个交点为C.
(1)、如图1,若 , , 求的长;(2)、如图2,正方形绕点B逆时针旋转,使点G正好落在上,求证:;(3)、如图3,在(2)条件下, , , 点M为直线上一动点,连接 , 过点作 , 垂足为点 , 直接写出的最小值为 .26. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线经过两点,与x轴的另一个交点为C. (1)、求抛物线的解析式.(2)、D为直线上方抛物线上一动点.
(1)、求抛物线的解析式.(2)、D为直线上方抛物线上一动点.①连接交于点E,若 , 求点D的坐标;
②是否存在点D,使得的度数恰好是的2倍?如果存在,请求出点D的坐标;如果不存在,请说明理由.