山东省济南市平阴区2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. ﹣6的相反数是( )A、﹣6 B、﹣ C、6 D、2. 左下图是一些完全相同的小正方体搭成的几何体的三视图 .这个几何体只能是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 中国科学技术大学利用“墨子号”科学实验卫星,首次实现在地球上相距1200公里的两个地面站之间的量子态远程传输,对于人类构建全球化量子信息处理和量子通信网络迈出重要一步,1200这个数用科学记数法可表示为( )A、 B、 C、 D、4. 已知直线 , 将含30°角的直角三角板按图所示摆放.若 , 则( )
3. 中国科学技术大学利用“墨子号”科学实验卫星,首次实现在地球上相距1200公里的两个地面站之间的量子态远程传输,对于人类构建全球化量子信息处理和量子通信网络迈出重要一步,1200这个数用科学记数法可表示为( )A、 B、 C、 D、4. 已知直线 , 将含30°角的直角三角板按图所示摆放.若 , 则( ) A、120° B、130° C、140° D、150°5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
A、120° B、130° C、140° D、150°5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 实数a,b在数轴上的位置如图所示,则 ( )
6. 实数a,b在数轴上的位置如图所示,则 ( )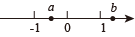 A、 B、 C、 D、7. 2022年2月20日北京冬奥会大幕落下,中国队在冰上、雪上项目中,共斩获9金4银2铜,创造中国队冬奥会历史最好成绩某校为普及冬奥知识,开展了校内冬奥知识竞赛活动,并评出一等奖3人.现欲从小明等3名一等奖获得者中任选2名参加全市冬奥知识竞赛,则小明被选到的概率为( )A、 B、 C、 D、8. 反比例函数与一次函数在同一坐标系中的大致图象可能是( )A、
A、 B、 C、 D、7. 2022年2月20日北京冬奥会大幕落下,中国队在冰上、雪上项目中,共斩获9金4银2铜,创造中国队冬奥会历史最好成绩某校为普及冬奥知识,开展了校内冬奥知识竞赛活动,并评出一等奖3人.现欲从小明等3名一等奖获得者中任选2名参加全市冬奥知识竞赛,则小明被选到的概率为( )A、 B、 C、 D、8. 反比例函数与一次函数在同一坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图所示,在中,按下列步骤作图:
9. 如图所示,在中,按下列步骤作图:第一步:在上分别截取 , 使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
 A、 B、 C、 D、10. 已知二次函数 , 若时,函数的最大值与最小值的差为4, 则a的值为( )A、 B、 C、或 D、1或
A、 B、 C、 D、10. 已知二次函数 , 若时,函数的最大值与最小值的差为4, 则a的值为( )A、 B、 C、或 D、1或二、填空题
-
11. 因式分解: .12. 如图,一块飞镖游戏板由大小相等的小正方形格子构成.向游戏板随机投掷一枚飞镖(每次飞镖均落在纸板上),击中阴影区域的概率是 .
 13. 计算: .14. 如图,将一个正六边形与一个正五边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠BEC= .
13. 计算: .14. 如图,将一个正六边形与一个正五边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠BEC= .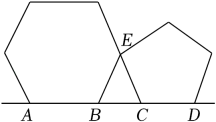 15. 如图,以边长为2的等边顶点A为圆心、一定的长为半径画弧,恰好与边相切,分别交于D,E,则图中阴影部分的面积是 .
15. 如图,以边长为2的等边顶点A为圆心、一定的长为半径画弧,恰好与边相切,分别交于D,E,则图中阴影部分的面积是 . 16. 平面直角坐标系中,若点P的坐标为 , 点Q的坐标为 , 其中m为常数,则称点Q是点P的m级派生点,例如点的3级派生点是 , 即 . 如图点是点的级派生点,点A在x轴上,且 , 则点A的坐标为 .
16. 平面直角坐标系中,若点P的坐标为 , 点Q的坐标为 , 其中m为常数,则称点Q是点P的m级派生点,例如点的3级派生点是 , 即 . 如图点是点的级派生点,点A在x轴上,且 , 则点A的坐标为 .
三、解答题
-
17. 计算:18. 解不等式组: , 并写出它的正整数解.19. 如图,在▱ABCD中,E、F分别是对角线BD上的两点.且BF=DE,求证:AF=CE.
 20. 第24届冬奥会于2022年2月20日在北京胜利闭幕.某校七、八年级各有500名学生.为了解这两个年级学生对本次冬奥会的关注程度,现从这两个年级各随机抽取n名学生进行冬奥会知识测试,将测试成绩按以下六组进行整理(得分用x表示):
20. 第24届冬奥会于2022年2月20日在北京胜利闭幕.某校七、八年级各有500名学生.为了解这两个年级学生对本次冬奥会的关注程度,现从这两个年级各随机抽取n名学生进行冬奥会知识测试,将测试成绩按以下六组进行整理(得分用x表示):A: , B: , C: ,
D: , E: , F: ,
并绘制七年级测试成绩频数直方图和八年级测试成绩扇形统计图,部分信息如下:

已知八年级测试成绩D组的全部数据如下:86,85,87,86,85,89,88
请根据以上信息,完成下列问题:
(1)、n= , a=;(2)、八年级测试成绩的中位数是﹔(3)、若测试成绩不低于90分,则认定该学生对冬奥会关注程度高.请估计该校七、八两个年级对冬奥会关注程度高的学生一共有多少人,并说明理由.21. 如图,小敏在数学实践活动中,利用所学知识对他所在小区居民楼AB的高度进行测量,从小敏家阳台C测得点A的仰角为33°,测得点B的俯角为45°,已知观测点到地面的高度CD=36m,求居民楼AB的高度(结果保留整数.参考数据:sin33°≈0.55,cos33°≈0.84,tan33°≈0.65).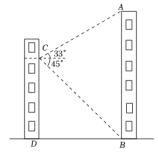 22. 如图, 内接于 , , 是 的直径, 是 延长线上一点,且 .
22. 如图, 内接于 , , 是 的直径, 是 延长线上一点,且 .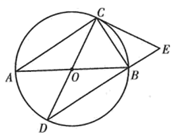 (1)、求证: 是 的切线;(2)、若 , ,求线段 的长.23. 小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)、求大本作业本与小本作业本每本各多少元?(2)、因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24. 如图,在平面直角坐标系中,菱形的对角线与交于点 , 轴于点E,正比例函数的图象与反比例函数的图象相交于A、P两点.
(1)、求证: 是 的切线;(2)、若 , ,求线段 的长.23. 小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.(1)、求大本作业本与小本作业本每本各多少元?(2)、因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?24. 如图,在平面直角坐标系中,菱形的对角线与交于点 , 轴于点E,正比例函数的图象与反比例函数的图象相交于A、P两点. (1)、求m、n的值;(2)、求证:;(3)、求的值.25. 如图1,已知和均为等腰直角三角形,点D、E分别在线段上, .
(1)、求m、n的值;(2)、求证:;(3)、求的值.25. 如图1,已知和均为等腰直角三角形,点D、E分别在线段上, .
 (1)、观察猜想:如图2,将绕点A逆时针旋转,连接 , 的延长线交于点F.当的延长线恰好经过点E时,点E与点F重合,此时,
(1)、观察猜想:如图2,将绕点A逆时针旋转,连接 , 的延长线交于点F.当的延长线恰好经过点E时,点E与点F重合,此时,
①的值为;
②的度数为度;
(2)、类比探究:如图3,继续旋转 , 点F与点E不重合时,上述结论是否仍然成立,请说明理由. (3)、拓展延伸:若 , , 当所在的直线垂直于时,请直接写出线段的长.26. 如图,在平面直角坐标系中,抛物线与直线交于点 , .
(3)、拓展延伸:若 , , 当所在的直线垂直于时,请直接写出线段的长.26. 如图,在平面直角坐标系中,抛物线与直线交于点 , .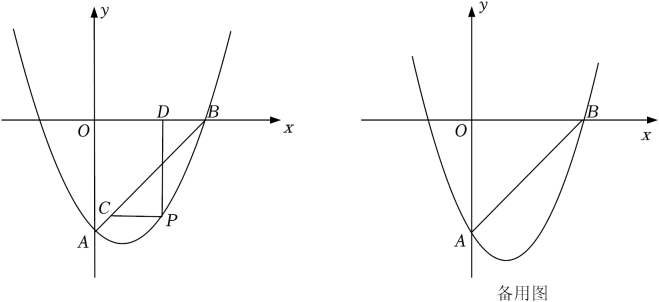 (1)、求该抛物线的函数表达式;(2)、点是直线下方抛物线上的一动点,过点作轴的平行线交于点 , 过点作轴的平行线交轴于点 , 求的最大值及此时点的坐标;(3)、在(2)中取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点 , 使得以点 , , , 为顶点的四边形是平行四边形,直接写出所有符合条件的点的坐标.
(1)、求该抛物线的函数表达式;(2)、点是直线下方抛物线上的一动点,过点作轴的平行线交于点 , 过点作轴的平行线交轴于点 , 求的最大值及此时点的坐标;(3)、在(2)中取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点 , 使得以点 , , , 为顶点的四边形是平行四边形,直接写出所有符合条件的点的坐标.