山东省东营市东营区2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
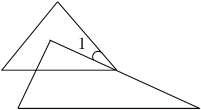
1. 的相反数是( )A、-1 B、1 C、-2023 D、20232. 下列计算正确的是( )A、 B、 C、 D、3. 将一副三角板如图所示放置,斜边平行,则的度数为( )
 A、 B、 C、 D、4. 一只蜘蛛爬到如图所示的一面墙上,停留位置是随机的,则停留在阴影区域上的概率是( )
A、 B、 C、 D、4. 一只蜘蛛爬到如图所示的一面墙上,停留位置是随机的,则停留在阴影区域上的概率是( ) A、 B、 C、 D、5. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为 , 则甲楼高度为( )
A、 B、 C、 D、5. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为 , 则甲楼高度为( ) A、15米 B、米 C、米 D、米6. 如图是一个机器零件的三视图,根据标注的尺寸,这个零件的表面积(单位:)是( )
A、15米 B、米 C、米 D、米6. 如图是一个机器零件的三视图,根据标注的尺寸,这个零件的表面积(单位:)是( ) A、 B、 C、 D、7. 如图,函数 和 的图象相交于点 ,则不等式 的解集为( )
A、 B、 C、 D、7. 如图,函数 和 的图象相交于点 ,则不等式 的解集为( )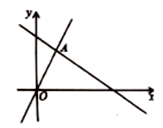 A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径画弧,分别交BA,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若AC=12,则在△ABD中AB边上的高为( )
A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径画弧,分别交BA,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若AC=12,则在△ABD中AB边上的高为( ) A、3 B、4 C、5 D、69. 如图1,在中, , 点D是边上的中点,点P从的顶点A出发,沿的路径以每秒1个单位长度的速度匀速运动到点D.线段的长度y随时间x变化的关系图象如图2所示,点N是曲线部分的最低点,则的面积为( )
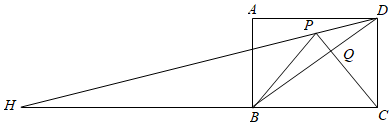
A、3 B、4 C、5 D、69. 如图1,在中, , 点D是边上的中点,点P从的顶点A出发,沿的路径以每秒1个单位长度的速度匀速运动到点D.线段的长度y随时间x变化的关系图象如图2所示,点N是曲线部分的最低点,则的面积为( ) A、4 B、 C、8 D、10. 如图,四边形是边长为1的正方形,是等边三角形,连接并延长交的延长线于点H,连接交于点Q,下列结论:
A、4 B、 C、8 D、10. 如图,四边形是边长为1的正方形,是等边三角形,连接并延长交的延长线于点H,连接交于点Q,下列结论:①;②;③;④ .
其中正确的有( )
 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
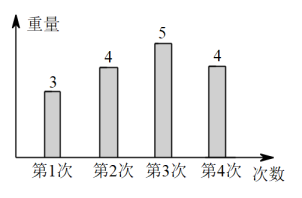
11. 2022年10月12日,“天宫课堂”第三课在中国空间站开讲,3名航天员演示了在微重力环境下毛细效应实验、水球变“懒”实验等,相应视频在某短视频平台的点赞量达到150万次,数据150万用科学记数法表示为 .12. 分解因式: .13. 如图所示的是莉莉次购买某水果的重量(单位,)的统计图,则次重量的中位数是 .
 14. 如图所示,已知圆的半径 , 以为边分别作正五边形和正六边形 , 则图中阴影部分的面积为(结果保留).
14. 如图所示,已知圆的半径 , 以为边分别作正五边形和正六边形 , 则图中阴影部分的面积为(结果保留). 15. 已知是一元二次方程的一个根,则代数式的值为 .16. 如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且 , 则EG的长是 .
15. 已知是一元二次方程的一个根,则代数式的值为 .16. 如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且 , 则EG的长是 . 17. 如图,等腰的底边长为6,面积是30,腰的垂直平分线分别交 , 边于点E,F,若点D为边的中点,点M为线段上一动点,则周长的最小值为 .
17. 如图,等腰的底边长为6,面积是30,腰的垂直平分线分别交 , 边于点E,F,若点D为边的中点,点M为线段上一动点,则周长的最小值为 . 18. 如图,在平面直角坐标系中,直线:与直线:交于点 , 过作x轴的垂线,垂足为 , 过作的平行线交于 , 过作x轴的垂线,垂足为 , 过作的平行线交于 , 过作x轴的垂线,垂足为…按此规律,则点的纵坐标为 .
18. 如图,在平面直角坐标系中,直线:与直线:交于点 , 过作x轴的垂线,垂足为 , 过作的平行线交于 , 过作x轴的垂线,垂足为 , 过作的平行线交于 , 过作x轴的垂线,垂足为…按此规律,则点的纵坐标为 .
三、解答题
-
19. 计算及先化简,再求值:(1)、计算:(2)、先化简,再求值: , 其中x从、、中选择一个适当的数代入.20. “端午节”吃粽子是我国流传了上千年的习俗.某班学生在“端午节”前组织了一次综合实践活动,购买了一些材料制作爱心粽,每人从自己制作的粽子中随机选取两个献给自己的父母,其余的全部送给敬老院的老人们,统计全班学生制作粽子的个数,将制作粽子数量相同的学生分为一组,全班学生可分为A,B,C,D四个组,各组每人制作的粽子个数分别为4,5,6,7.根据如图不完整的统计图解答下列问题:
 (1)、请补全上面两个统计图;(不写过程)(2)、该班学生制作粽子个数的平均数是个;(3)、若制作的粽子有红枣馅(记为M)和蛋黄馅(记为N)两种,该班小明同学制作这两种粽子各两个混放在一起,请用列表或画树形图的方法求小明献给父母的粽子馅料不同的概率.21. 如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC, .
(1)、请补全上面两个统计图;(不写过程)(2)、该班学生制作粽子个数的平均数是个;(3)、若制作的粽子有红枣馅(记为M)和蛋黄馅(记为N)两种,该班小明同学制作这两种粽子各两个混放在一起,请用列表或画树形图的方法求小明献给父母的粽子馅料不同的概率.21. 如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC, .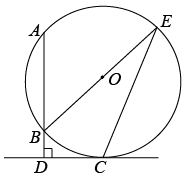 (1)、求证:CD是⊙O的切线;(2)、若 , , 求AB的长.22. 党的二十大报告,深刻阐述了推动绿色发展,促进人与自然和谐共生的理念,尊重自然、顺应自然、保护自然,是全面建设社会主义现代化国家的内在要求.为响应党的号召,东营市政府欲购进一批风景树进行绿化,已知购进A种风景树4万棵,B种风景树3万棵,共需要380万元;购进A种风景树8万棵,B种风景树5万棵,共需要700万元.(1)、问A,B两种风景树每棵的进价分别是多少元?(2)、东营市政府计划用不超过5460万元购进A,B两种风景树共100万棵,其中要求A风景树的数量不多于58万棵,则共有几种购买方案?23. 如图,一次函数y=kx+b(k≠0)的图像与反比例函数y=(m≠0)的图像相交于点A(1,2),B(a,−1).
(1)、求证:CD是⊙O的切线;(2)、若 , , 求AB的长.22. 党的二十大报告,深刻阐述了推动绿色发展,促进人与自然和谐共生的理念,尊重自然、顺应自然、保护自然,是全面建设社会主义现代化国家的内在要求.为响应党的号召,东营市政府欲购进一批风景树进行绿化,已知购进A种风景树4万棵,B种风景树3万棵,共需要380万元;购进A种风景树8万棵,B种风景树5万棵,共需要700万元.(1)、问A,B两种风景树每棵的进价分别是多少元?(2)、东营市政府计划用不超过5460万元购进A,B两种风景树共100万棵,其中要求A风景树的数量不多于58万棵,则共有几种购买方案?23. 如图,一次函数y=kx+b(k≠0)的图像与反比例函数y=(m≠0)的图像相交于点A(1,2),B(a,−1). (1)、求反比例函数和一次函数的解析式;(2)、若直线y=kx+b(k≠0)与x轴交于点C,x轴上是否存在一点P,使S△APC=4?若存在,请求出点P坐标;若不存在,说明理由.24. 如图,已知二次函数的图象与x轴交于和两点,与y轴交于点 , 直线经过点A,且与y轴交于点D,与抛物线交于点E.
(1)、求反比例函数和一次函数的解析式;(2)、若直线y=kx+b(k≠0)与x轴交于点C,x轴上是否存在一点P,使S△APC=4?若存在,请求出点P坐标;若不存在,说明理由.24. 如图,已知二次函数的图象与x轴交于和两点,与y轴交于点 , 直线经过点A,且与y轴交于点D,与抛物线交于点E. (1)、求抛物线的解析式;(2)、如图1,点M在下方的抛物线上运动,求的面积最大值;(3)、如图2,在y轴上是否存在点P,使得以D、E、P为顶点的三角形与相似,若存在,求出点P的坐标;若不存在,试说明理由.25.(1)、问题:如图①,在中, , D为边上一点(不与点B,C重合),将线段绕点A逆时针旋转得到 , 连接 , 则线段和线段的数量关系是 , 位置关系是;
(1)、求抛物线的解析式;(2)、如图1,点M在下方的抛物线上运动,求的面积最大值;(3)、如图2,在y轴上是否存在点P,使得以D、E、P为顶点的三角形与相似,若存在,求出点P的坐标;若不存在,试说明理由.25.(1)、问题:如图①,在中, , D为边上一点(不与点B,C重合),将线段绕点A逆时针旋转得到 , 连接 , 则线段和线段的数量关系是 , 位置关系是; (2)、探索:如图②,在与中, , , 将绕点A旋转,使点D落在边上,试探索线段 , , 之间满足的等量关系,并证明结论;
(2)、探索:如图②,在与中, , , 将绕点A旋转,使点D落在边上,试探索线段 , , 之间满足的等量关系,并证明结论; (3)、应用:如图3,在四边形中, . 若 , , 求的长.
(3)、应用:如图3,在四边形中, . 若 , , 求的长.