山东省滨州市阳信县2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 如果规定收入为正,支出为负,收入3元记作3元,那么支出8元记作( )A、5元 B、元 C、11元 D、元2. 如果关于x的不等式的解集为 , 则a的值可以是( )A、1 B、0 C、 D、3. 下列运算正确的是( )A、3a2•2a3=6a5 B、a3+4a= C、(a2)3=a5 D、-2(a+b)=-2a+2b4. 已知a,b满足方程组 则a+b的值为( )
A、﹣4 B、4 C、﹣2 D、25. 如图,直线 ,且 于点 ,若 ,则 的度数为( )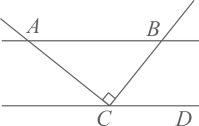 A、65° B、55° C、45° D、35°6. 如图,与分别相切于点A,B, , 则( )
A、65° B、55° C、45° D、35°6. 如图,与分别相切于点A,B, , 则( ) A、 B、2 C、 D、37. 若 , ,则以 , 为根的一元二次方程是( )A、 B、 C、 D、8. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西方向上,在海岛B的北偏西方向上,则海岛B到灯塔C的距离是( )A、15海里 B、20海里 C、30海里 D、60海里9. 二次函数的图象如图所示,下列选项错误的是( )
A、 B、2 C、 D、37. 若 , ,则以 , 为根的一元二次方程是( )A、 B、 C、 D、8. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏西方向上,在海岛B的北偏西方向上,则海岛B到灯塔C的距离是( )A、15海里 B、20海里 C、30海里 D、60海里9. 二次函数的图象如图所示,下列选项错误的是( ) A、 B、时,y随x的增大而增大 C、 D、方程的根是 ,10. 在2021年初中毕业生体育测试中,某校随机抽取了10名男生的引体向上成绩,将这组数据整理后制成如下统计表:
A、 B、时,y随x的增大而增大 C、 D、方程的根是 ,10. 在2021年初中毕业生体育测试中,某校随机抽取了10名男生的引体向上成绩,将这组数据整理后制成如下统计表:成绩(次)
12
11
10
9
人数(名)
1
3
4
2
关于这组数据的结论错误的是( )
A、中位数是10.5 B、平均数是10.3 C、众数是10 D、方差是0.8111. 如图,一次函数与反比例函数的图象交于点 , .则关于x的不等式的解集是( ) A、或 B、或 C、或 D、或12. 函数叫做高斯函数,其中x为任意实数,表示不超过x的最大整数.定义 , 则下列说法正确的个数为( )
A、或 B、或 C、或 D、或12. 函数叫做高斯函数,其中x为任意实数,表示不超过x的最大整数.定义 , 则下列说法正确的个数为( )①;
②;
③高斯函数中,当时,x的取值范围是;
④函数中,当时, .
A、0 B、1 C、2 D、3二、填空题
-
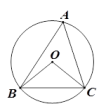
13. 在实数 , 中最小的实数是 .14. 分解因式:ax2-9a= .15. 不等式组 的解集是 .16. 如图,⊙O是△ABC的外接圆,∠A=45°,则cos∠OCB的值是.
 17. 如图,在 中, ,分别以点A , B为圆心,以大于 长为半径画弧,两弧交于点D , E . 作直线DE , 交BC于点M . 分别以点A , C为圆心,以大于 长为半径画弧,两弧交于点F , G . 作直线FG , 交BC于点N . 连接AM , AN . 若 ,则 .
17. 如图,在 中, ,分别以点A , B为圆心,以大于 长为半径画弧,两弧交于点D , E . 作直线DE , 交BC于点M . 分别以点A , C为圆心,以大于 长为半径画弧,两弧交于点F , G . 作直线FG , 交BC于点N . 连接AM , AN . 若 ,则 .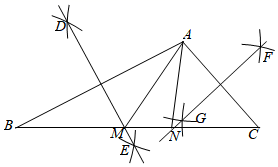 18. 如图,菱形中,点是边的中点,垂直交的延长线于点 , 若 , , 则菱形的边长是 .
18. 如图,菱形中,点是边的中点,垂直交的延长线于点 , 若 , , 则菱形的边长是 .
三、解答题
-
19. 先化简,再求值: , 其中 .20. 某校为了解九年级学生体质健康情况,随机抽取了部分学生进行体能测试,根据测试结果绘制了不完整的条形统计图和扇形统计图,请回答下列问题:
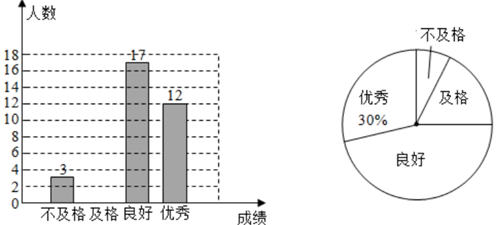 (1)、在这次调查中,“优秀”所在扇形的圆心角的度数是;(2)、请补全条形统计图;(3)、若该校九年级共有学生1200人,则估计该校“良好”的人数是;(4)、已知“不合格”的3名学生中有2名男生、1名女生,如果从中随机抽取两名同学进行体能加试,请用列表法或画树状图的方法,求抽到两名男生的概率多少?21. 打油茶是广西少数民族特有的一种民俗,某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)、在这次调查中,“优秀”所在扇形的圆心角的度数是;(2)、请补全条形统计图;(3)、若该校九年级共有学生1200人,则估计该校“良好”的人数是;(4)、已知“不合格”的3名学生中有2名男生、1名女生,如果从中随机抽取两名同学进行体能加试,请用列表法或画树状图的方法,求抽到两名男生的概率多少?21. 打油茶是广西少数民族特有的一种民俗,某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.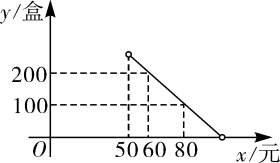 (1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.22. 如图,直线交于A、B两点,是的直径,点C为上一点,且平分 , 过C作 , 垂足为D.
(1)、求y与x的函数解析式,并写出自变量x的取值范围;(2)、当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.22. 如图,直线交于A、B两点,是的直径,点C为上一点,且平分 , 过C作 , 垂足为D. (1)、求证:为的切线;(2)、若 , 求的长.
(1)、求证:为的切线;(2)、若 , 求的长.