压轴题06 立体几何(选填题)-【考前冲刺】2023年高考数学压轴题专项训练(全国通用)
试卷更新日期:2023-05-04 类型:三轮冲刺
一、单选题
-
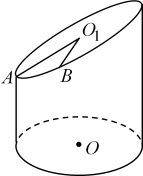
1. 已知等腰直角的斜边分别为上的动点,将沿折起,使点到达点的位置,且平面平面.若点均在球的球面上,则球表面积的最小值为( )A、 B、 C、 D、2. 一底面半径为1的圆柱,被一个与底面成45°角的平面所截(如图),为底面圆的中心,为截面的中心,为截面上距离底面最小的点,到圆柱底面的距离为1,为截面图形弧上的一点,且 , 则点到底面的距离是( )
 A、 B、 C、 D、3. 已知圆锥的底面半径为 , 高为 , 当其内接正四棱柱的体积最大时,该正四棱柱的外接球的表面积(单位:)为( )A、 B、 C、 D、4. 在棱长为6的正方体中, , 分别为 , 的中点,则三棱锥外接球的表面积为( )A、 B、 C、 D、5. 鲁班锁是我国传统的智力玩具,起源于中国古代建筑中的榫卯结构,其内部的凹凸部分啮合十分精巧.图1是一种鲁班锁玩具,图2是其直观图.它的表面由八个正三角形和六个正八边形构成,其中每条棱长均为2.若该玩具可以在一个正方体内任意转动(忽略摩擦),则此正方体表面积的最小值为( )
A、 B、 C、 D、3. 已知圆锥的底面半径为 , 高为 , 当其内接正四棱柱的体积最大时,该正四棱柱的外接球的表面积(单位:)为( )A、 B、 C、 D、4. 在棱长为6的正方体中, , 分别为 , 的中点,则三棱锥外接球的表面积为( )A、 B、 C、 D、5. 鲁班锁是我国传统的智力玩具,起源于中国古代建筑中的榫卯结构,其内部的凹凸部分啮合十分精巧.图1是一种鲁班锁玩具,图2是其直观图.它的表面由八个正三角形和六个正八边形构成,其中每条棱长均为2.若该玩具可以在一个正方体内任意转动(忽略摩擦),则此正方体表面积的最小值为( ) A、 B、 C、 D、6. 已知三棱锥的四个顶点都在球的球面上, , , 则球的表面积为( )A、 B、 C、 D、7. 盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商准备将棱长为的正四面体的魔方放入正方体盲盒内,为节约成本,使得魔方能够放入盲盒且盲盒棱长最小时,盲盒内剩余空间的体积为( )A、 B、 C、 D、8. 如图,中, , , 为的中点,将沿折叠成三棱锥 , 则当该三棱锥体积最大时它的外接球的表面积为( )
A、 B、 C、 D、6. 已知三棱锥的四个顶点都在球的球面上, , , 则球的表面积为( )A、 B、 C、 D、7. 盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商准备将棱长为的正四面体的魔方放入正方体盲盒内,为节约成本,使得魔方能够放入盲盒且盲盒棱长最小时,盲盒内剩余空间的体积为( )A、 B、 C、 D、8. 如图,中, , , 为的中点,将沿折叠成三棱锥 , 则当该三棱锥体积最大时它的外接球的表面积为( ) A、 B、 C、 D、9. 在三棱锥中,平面平面BCD,是以CD为斜边的等腰直角三角形,M为CD中点, , , 则该三棱锥的外接球的表面积为( )A、 B、 C、 D、10. 在正方体中, , 为棱的四等分点(靠近点),为棱的四等分点(靠近点),过点 , , 作该正方体的截面,则该截面的周长是( )A、 B、 C、 D、11. 《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”.现有一个刍甍如图所示,底面为正方形,平面 , 四边形 , 为两个全等的等腰梯形, , 且 , 则此刍甍的外接球的表面积为( )
A、 B、 C、 D、9. 在三棱锥中,平面平面BCD,是以CD为斜边的等腰直角三角形,M为CD中点, , , 则该三棱锥的外接球的表面积为( )A、 B、 C、 D、10. 在正方体中, , 为棱的四等分点(靠近点),为棱的四等分点(靠近点),过点 , , 作该正方体的截面,则该截面的周长是( )A、 B、 C、 D、11. 《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”.现有一个刍甍如图所示,底面为正方形,平面 , 四边形 , 为两个全等的等腰梯形, , 且 , 则此刍甍的外接球的表面积为( ) A、 B、 C、 D、12. 已知正方体的棱长为4,M,N分别是侧面和侧面的中心,过点M的平面与直线ND垂直,平面截正方体所得的截面记为S,则S的面积为( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知正方体的棱长为4,M,N分别是侧面和侧面的中心,过点M的平面与直线ND垂直,平面截正方体所得的截面记为S,则S的面积为( )A、 B、 C、 D、二、多选题
-
13. 某学校课外社团活动课上,数学兴趣小组进行了一次有趣的数学实验操作,课题名称“不用尺规等工具,探究水面高度”.如图甲,是一个水平放置的装有一定量水的四棱锥密闭容器(容器材料厚度不计),底面为平行四边形,设棱锥高为 , 体积为 , 现将容器以棱为轴向左侧倾斜,如图乙,这时水面恰好经过 , 其中分别为棱的中点,则( )
 A、水的体积为 B、水的体积为 C、图甲中的水面高度为 D、图甲中的水面高度为14. 已知为圆锥底面圆的直径,点是圆上异于 , 的一点,为的中点, , 圆锥的侧面积为 , 则下列说法正确的是( )A、圆上存在点使平面 B、圆上存在点使平面 C、圆锥的外接球表面积为 D、棱长为的正四面体在圆锥内可以任意转动15. 在三棱锥中, , , , 分别是 , , , 的重心.则下列命题中正确的有( )A、平面 B、 C、四条直线 , , , 相交于一点 D、16. 已知三棱锥的所有棱长均相等,其外接球的球心为O.点E满足 , 过点E作平行于和的平面 , 分别与棱相交于点 , 则( )A、当时,平面经过球心O B、四边形的周长随的变化而变化 C、当时,四棱锥的体积取得最大值 D、设四棱锥的体积为 , 则17. 勒洛Franz Reuleaux(1829~1905),德国机械工程专家,机构运动学的创始人.他所著的《理论运动学》对机械元件的运动过程进行了系统的分析,成为机械工程方面的名著.勒洛四面体是一个非常神奇的“四面体”,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的相交部分围成的几何体.如图所示,设正四面体的棱长为2,则下列说法正确的是( )
A、水的体积为 B、水的体积为 C、图甲中的水面高度为 D、图甲中的水面高度为14. 已知为圆锥底面圆的直径,点是圆上异于 , 的一点,为的中点, , 圆锥的侧面积为 , 则下列说法正确的是( )A、圆上存在点使平面 B、圆上存在点使平面 C、圆锥的外接球表面积为 D、棱长为的正四面体在圆锥内可以任意转动15. 在三棱锥中, , , , 分别是 , , , 的重心.则下列命题中正确的有( )A、平面 B、 C、四条直线 , , , 相交于一点 D、16. 已知三棱锥的所有棱长均相等,其外接球的球心为O.点E满足 , 过点E作平行于和的平面 , 分别与棱相交于点 , 则( )A、当时,平面经过球心O B、四边形的周长随的变化而变化 C、当时,四棱锥的体积取得最大值 D、设四棱锥的体积为 , 则17. 勒洛Franz Reuleaux(1829~1905),德国机械工程专家,机构运动学的创始人.他所著的《理论运动学》对机械元件的运动过程进行了系统的分析,成为机械工程方面的名著.勒洛四面体是一个非常神奇的“四面体”,它能在两个平行平面间自由转动,并且始终保持与两平面都接触,因此它能像球一样来回滚动.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的相交部分围成的几何体.如图所示,设正四面体的棱长为2,则下列说法正确的是( )
 A、勒洛四面体能够容纳的最大球的半径为 B、勒洛四面体被平面截得的截面面积是 C、勒洛四面体表面上交线的长度为 D、勒洛四面体表面上任意两点间的距离可能大于218. 如图的六面体中,CA=CB=CD=1,AB=BD=AD=AE=BE=DE= , 则( )
A、勒洛四面体能够容纳的最大球的半径为 B、勒洛四面体被平面截得的截面面积是 C、勒洛四面体表面上交线的长度为 D、勒洛四面体表面上任意两点间的距离可能大于218. 如图的六面体中,CA=CB=CD=1,AB=BD=AD=AE=BE=DE= , 则( )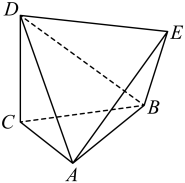 A、CD⊥平面ABC B、AC与BE所成角的大小为 C、 D、该六面体外接球的表面积为3π19. 在正方体中,为线段上的动点,则( )A、平面 B、平面 C、三棱锥的体积为定值 D、直线与所成角的取值范围是20. 如图,正四棱柱中, , 动点P满足 , 且.则下列说法正确的是( )
A、CD⊥平面ABC B、AC与BE所成角的大小为 C、 D、该六面体外接球的表面积为3π19. 在正方体中,为线段上的动点,则( )A、平面 B、平面 C、三棱锥的体积为定值 D、直线与所成角的取值范围是20. 如图,正四棱柱中, , 动点P满足 , 且.则下列说法正确的是( ) A、当时,直线平面 B、当时,的最小值为 C、若直线与所成角为 , 则动点P的轨迹长为 D、当时,三棱锥外接球半径的取值范围是21. 如图,已知正三棱台的上、下底面边长分别为2和3,侧棱长为1,点P在侧面内运动(包含边界),且AP与平面所成角的正切值为 , 则( )
A、当时,直线平面 B、当时,的最小值为 C、若直线与所成角为 , 则动点P的轨迹长为 D、当时,三棱锥外接球半径的取值范围是21. 如图,已知正三棱台的上、下底面边长分别为2和3,侧棱长为1,点P在侧面内运动(包含边界),且AP与平面所成角的正切值为 , 则( ) A、CP长度的最小值为 B、存在点P,使得 C、存在点P,存在点 , 使得 D、所有满足条件的动线段AP形成的曲面面积为22. 已知圆锥SO(O是底面圆的圆心,S是圆锥的顶点)的母线长为 , 高为 . 若P,Q为底面圆周上任意两点,则下列结论正确的是( )A、三角形面积的最大值为 B、三棱锥体积的最大值 C、四面体外接球表面积的最小值为11 D、直线SP与平面所成角的余弦值的最小值为
A、CP长度的最小值为 B、存在点P,使得 C、存在点P,存在点 , 使得 D、所有满足条件的动线段AP形成的曲面面积为22. 已知圆锥SO(O是底面圆的圆心,S是圆锥的顶点)的母线长为 , 高为 . 若P,Q为底面圆周上任意两点,则下列结论正确的是( )A、三角形面积的最大值为 B、三棱锥体积的最大值 C、四面体外接球表面积的最小值为11 D、直线SP与平面所成角的余弦值的最小值为三、填空题
-
23. 三棱锥中,平面 , , , 点在三棱锥外接球的球面上,且 , 则的最小值为.24. 在棱长为4的正方体中,点是棱上一点,且.过三点、、的平面截该正方体的内切球,所得截面圆面积的大小为.25. 在棱长为1的正方体中,为底面的中心, , , 为线段的中点,则下列命题中正确的序号为.

①与共面;
②三棱锥的体积跟的取值无关;
③当时,过三点的平面截正方体所得截面的周长为;
④时,.
26. 已知正四棱锥的所有棱长都为1,点在侧棱上,过点且垂直于的平面截该棱锥,得到截面多边形 , 则的边数至多为 , 的面积的最大值为.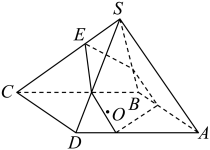 27. 在正方体 中,点E为线段 上的动点,现有下面四个命题:
27. 在正方体 中,点E为线段 上的动点,现有下面四个命题:①点E到直线AB的距离为定值; ②直线DE与直线AC所成角为定值;
③三棱锥 的外接球体积为定值; ④三棱锥 的体积为定值.
其中所有真命题的序号是 .
28. 如图,在正方体中,M、N分别是棱、的中点,P是棱上靠近的四等分点,过M、N、P三点的平面交棱于Q,记 , 则 . 若平面将正方体截成两部分体积分别为、 , 则 . 29. 在三棱锥中,顶点P在底面的投影为O,点O到侧面 , 侧面 , 侧面的距离均为d,若 , . , 且是锐角三角形,则三棱锥体积的取值范围为 .30. 如图,在正方体中,点F是棱上的一个动点,平面交棱于点E,则下列正确说法的序号是.
29. 在三棱锥中,顶点P在底面的投影为O,点O到侧面 , 侧面 , 侧面的距离均为d,若 , . , 且是锐角三角形,则三棱锥体积的取值范围为 .30. 如图,在正方体中,点F是棱上的一个动点,平面交棱于点E,则下列正确说法的序号是.
①存在点F使得平面;
②存在点F使得平面;
③对于任意的点F,都有;
④对于任意的点F三棱锥的体积均不变.
31. 如图,在棱长为2的正方体中,点E,F,G分别是棱BC, , 的中点,点P为底面A1B1C1D1上任意一点.若P与重合,则三棱锥E-PFG的体积是;若直线BP与平面EFG无公共点,则BP的最小值是 . 32. 如图直角梯形中, , , , 在等腰直角三角形中, , 则向量在向量上的投影向量的模为;若 , 分别为线段 , 上的动点,且 , 则的最小值为 .
32. 如图直角梯形中, , , , 在等腰直角三角形中, , 则向量在向量上的投影向量的模为;若 , 分别为线段 , 上的动点,且 , 则的最小值为 .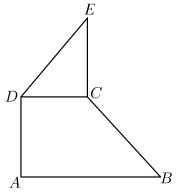 33. 如图,将正四面体每条棱三等分,截去顶角所在的小正四面体,余下的多面体就成为一个半正多面体,亦称“阿基米德体”.点A,B,M是该多面体的三个顶点,点N是该多面体外接球表面上的动点,且总满足 , 若 , 则该多面体的表面积为;点N轨迹的长度为 .
33. 如图,将正四面体每条棱三等分,截去顶角所在的小正四面体,余下的多面体就成为一个半正多面体,亦称“阿基米德体”.点A,B,M是该多面体的三个顶点,点N是该多面体外接球表面上的动点,且总满足 , 若 , 则该多面体的表面积为;点N轨迹的长度为 .
