压轴题04 解三角形(选填题)-【考前冲刺】2023年高考数学压轴题专项训练(全国通用)
试卷更新日期:2023-05-04 类型:三轮冲刺
一、单选题
-
1. 在中,为上一点,且 , , , 则( )A、 B、 C、 D、2. 在中,角 , , 所对的边分别为 , , , 若 , , 成等差数列, , 则( )A、 B、 C、 D、3. 在中,D是BC边的中点,且 , , , 则的形状为( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定4. 锐角是单位圆的内接三角形,角的对边分别为 , 且 , 则等于( )A、2 B、 C、 D、15. 已知点是椭圆上一点,椭圆的左、右焦点分别为、 , 且 , 则的面积为( )A、6 B、12 C、 D、6. 在中,角A,B和C所对的边长为a,b和c,面积为 , 且为钝角,的取值范围是( )A、 B、 C、 D、7. 已知中,角的对边分别为.若 , 则的最大值为( )A、 B、 C、 D、8. 已知 , , 是圆上的一个动点,则的最大值为( )A、 B、 C、 D、9. 的内角A,B,C的对边分别为a,b,c.已知 , , , 则的面积为( )A、 B、 C、1 D、10. 在 中,设 , , 分别为角 , , 对应的边,记 的面积为 ,且 ,则 的最大值为( )A、 B、 C、 D、11. 设 的内角 , , 的对边分别为 , , ,若 , , ,则 的面积为( )A、 B、 C、4 D、12. 已知四边形ABCD是圆内接四边形, ,则ABCD的周长取最大值时,四边形ABCD的面积为( )A、 B、 C、 D、13. 在 中,角A,B,C的对边分别为a,b,c,a=csinB,则tanA的最大值为( )A、1 B、 C、 D、14. 在平面四边形ABCD中,AB=1,AD=4,BC=CD=2,则四边形ABCD面积的最大值为( )A、 B、 C、 D、15. 已知△ABC的三边分别为a , b , c , 若满足a2+b2+2c2=8,则△ABC面积的最大值为( )A、 B、 C、 D、
二、多选题
-
16. 平面内到两定点距离之积为常数的点的轨迹称为卡西尼卵形线,它是1675年卡西尼在研究土星及其卫星的运行规律时发现的,已知在平面直角坐标系中, , , 动点P满足 , 则下列结论正确的是( )A、点的横坐标的取值范围是 B、的取值范围是 C、面积的最大值为 D、的取值范围是17. 已知圆锥SO(O是底面圆的圆心,S是圆锥的顶点)的母线长为 , 高为 . 若P,Q为底面圆周上任意两点,则下列结论正确的是( )A、三角形面积的最大值为 B、三棱锥体积的最大值 C、四面体外接球表面积的最小值为11 D、直线SP与平面所成角的余弦值的最小值为18. 在 中, , 分别是 , 的中点,且 , ,则( )A、 面积最大值是12 B、 C、 不可能是5 D、
三、填空题
-
19. 在中, , , , 是所在平面内任意一点,则的最小值是.20. 已知的三边长分别为4、5、7,记的三个内角的正切值所组成的集合为 , 则集合中的最大元素为.21. 已知在中,角 , , 的对边分别为 , , , , 是的中点,若 , 则的最大值为.22. 在△中,角 , , 所对的边分别为 , , . 若 , , 则△面积的最小值是 .23. 2022年3月,中共中央办公厅、国务院办公厅印发了《关于构建更高水平的全民健身公共服务体系的意见》,再次强调持续推进体育公园建设.如图,某市拟建造一个扇形体育公园,其中 , 千米.现需要在 , OB,上分别取一点D,E,F,建造三条健走长廊DE,DF,EF,若 , , 则的最大值为千米.
 24. 如图,在 中, , , ,点 是边 (端点除外)上的一动点.若将 沿直线 翻折,能使点 在平面 内的射影 落在 的内部(不包含边界),且 .设 ,则t的取值范围是.
24. 如图,在 中, , , ,点 是边 (端点除外)上的一动点.若将 沿直线 翻折,能使点 在平面 内的射影 落在 的内部(不包含边界),且 .设 ,则t的取值范围是.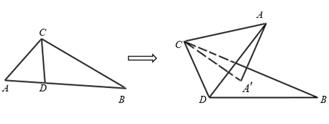 25. 中,为边上的中线, , 则的取值范围是 .
25. 中,为边上的中线, , 则的取值范围是 .