人教版初中数学几何辅助线进阶训练——菱形的辅助线(不含相似)
试卷更新日期:2023-05-03 类型:复习试卷
一、阶段一(较易)
-
1. 如图,菱形中, , 为中点, , , , 交于点 , 交于点.
 (1)、求证:四边形是矩形.(2)、求的度数.(3)、求菱形的面积.2. 在中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)、求证:四边形是矩形.(2)、求的度数.(3)、求菱形的面积.2. 在中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F. (1)、求证:;(2)、证明:四边形ADCF是菱形:(3)、若AC=3,AB=4,求菱形ADCF的面积.3. 如图,四边形为菱形,点E是的中点,点F,H是对角线上两点,且 , 点G在边上.若四边形是矩形,则菱形的周长为 .
(1)、求证:;(2)、证明:四边形ADCF是菱形:(3)、若AC=3,AB=4,求菱形ADCF的面积.3. 如图,四边形为菱形,点E是的中点,点F,H是对角线上两点,且 , 点G在边上.若四边形是矩形,则菱形的周长为 . 4. 如图1,平行四边形中,点E、点F分别是上的点,连接 , .
4. 如图1,平行四边形中,点E、点F分别是上的点,连接 , .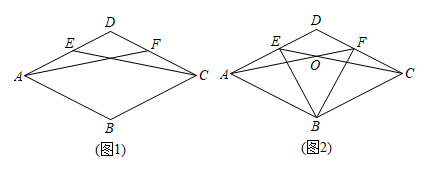 (1)、求证:四边形是菱形.(2)、如图2,当点E是AD中点时,与交于点O,连接 , 请直接写出图2中四个三角形,使写出的每个三角形的面积等于面积3倍.5. 如图,在菱形中, , 点F为的中点,于E,则的长为( )
(1)、求证:四边形是菱形.(2)、如图2,当点E是AD中点时,与交于点O,连接 , 请直接写出图2中四个三角形,使写出的每个三角形的面积等于面积3倍.5. 如图,在菱形中, , 点F为的中点,于E,则的长为( ) A、 B、 C、 D、6. 如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( )
A、 B、 C、 D、6. 如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( ) A、15 B、20 C、 D、7. 如图,四边形是平行四边形,对角线 , 交于点O, , .
A、15 B、20 C、 D、7. 如图,四边形是平行四边形,对角线 , 交于点O, , . (1)、求证:四边形是菱形.(2)、若 , , 求四边形的面积.8. 如图,在菱形中,点、分别是、的中点,连接交对角线于点 , 连接若 , , 则的长为 .
(1)、求证:四边形是菱形.(2)、若 , , 求四边形的面积.8. 如图,在菱形中,点、分别是、的中点,连接交对角线于点 , 连接若 , , 则的长为 . 9. 如图,菱形ABCD中, , AD的垂直平分线交对角线BD于点P,垂足为N,连结CP,则∠BPC=度.
9. 如图,菱形ABCD中, , AD的垂直平分线交对角线BD于点P,垂足为N,连结CP,则∠BPC=度. 10. 如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
10. 如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.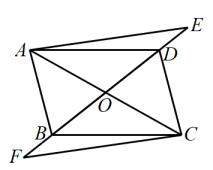 (1)、求证:△ADE≌△CBF;(2)、试连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
(1)、求证:△ADE≌△CBF;(2)、试连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.二、阶段二(中等)
-
11. 如图所示,在菱形ABCD中,AB=6,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
 A、4 B、 C、3 D、12. 如图,在矩形中, , , 点在边上,点在边上,点、在对角线上,若四边形是菱形.则的长是( )
A、4 B、 C、3 D、12. 如图,在矩形中, , , 点在边上,点在边上,点、在对角线上,若四边形是菱形.则的长是( )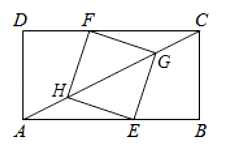 A、15 B、20 C、 D、13. 如图, , 点 , 分别在 , 上,连接 , 、的平分线交于点 , 、的平分线交于点 .
A、15 B、20 C、 D、13. 如图, , 点 , 分别在 , 上,连接 , 、的平分线交于点 , 、的平分线交于点 . (1)、求证:四边形是矩形;(2)、过作 , 分别交 , 于点 , , 过作 , 分别交 , 于点 , , 得到四边形 , 此时,求证四边形是菱形.14. 如图,菱形ABCD的边长是4,∠A=60°,点G为AB的中点,以BG为边作菱形BEFG,其中点E在CB的延长线上,点P为FD的中点,连接PB.则PB= .
(1)、求证:四边形是矩形;(2)、过作 , 分别交 , 于点 , , 过作 , 分别交 , 于点 , , 得到四边形 , 此时,求证四边形是菱形.14. 如图,菱形ABCD的边长是4,∠A=60°,点G为AB的中点,以BG为边作菱形BEFG,其中点E在CB的延长线上,点P为FD的中点,连接PB.则PB= . 15. 如图,菱形ABCD的对角线AC与BD交于点O,点E是AD边上一点,且 .若 , ,则AE的长是 .
15. 如图,菱形ABCD的对角线AC与BD交于点O,点E是AD边上一点,且 .若 , ,则AE的长是 . 16. 如图,在平行四边形 中, , 于点 , 为 的中点,连结 , ,下列结论:① ,② ;③ ;④ ,其中正确结论的个数共有( )
16. 如图,在平行四边形 中, , 于点 , 为 的中点,连结 , ,下列结论:① ,② ;③ ;④ ,其中正确结论的个数共有( ) A、1个 B、2个 C、3个 D、4个17. ▱ ABCD 中, ∠BAD的平分线交直线 BC 于点 E,线 DC于点 F
A、1个 B、2个 C、3个 D、4个17. ▱ ABCD 中, ∠BAD的平分线交直线 BC 于点 E,线 DC于点 F (1)、求证: ;(2)、若 , , ,求 .18. (问题发现)数学小组成员小明做作业时遇到以下问题:
(1)、求证: ;(2)、若 , , ,求 .18. (问题发现)数学小组成员小明做作业时遇到以下问题:


图1 图2 图3
(1)、若四边形 是菱形, ,点 是射线 上一动点,以 为边向右侧作等边 ,如图1,当点E在菱形 内部或边上时,连接 ,则 与 有怎样的数量关系?请直接写出你的猜想;(2)、(类比探究)数学小组对该问题进行进一步探究:若四边形 是正方形,点P是射线 上一动点,以 为直角边在 边的右侧作等腰 ,其中 .
①如图2,当点 在对角线 上时,小组发现点 恰好在射线 上,求 与 之间的数量关系(过程只用说明点 在线段 上的情况即可);
②如图3,当P是对角线 的延长线上一动点时,小组发现点 恰好在射线 上,连接 ,若 ,求 的面积.
19. 在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE,EF。 (1)、如图1,当E是线段AC的中点时,BE和EF的数量关系是;(2)、如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中 的结论是否成立?若成立,请给予证明:若不成立,请说明理由;(3)、如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由。20. 如图,菱形ABCD中,AB=4,∠ABC=120°,过对角线AC延长线上的一点P分别作AD、DC延长线的垂线,垂足分别为E、F,则PE-PF= 。
(1)、如图1,当E是线段AC的中点时,BE和EF的数量关系是;(2)、如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中 的结论是否成立?若成立,请给予证明:若不成立,请说明理由;(3)、如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由。20. 如图,菱形ABCD中,AB=4,∠ABC=120°,过对角线AC延长线上的一点P分别作AD、DC延长线的垂线,垂足分别为E、F,则PE-PF= 。
三、阶段三(较难)
-
21. 如图,在平面直角坐标系中,菱形的对角线上有P,Q两个动点,且 , 已知点 , 当周长最小时,点P的坐标为.
 22. 在菱形中, , P是直线上一动点,以为边向右侧作等边(A,P,E按逆时针排列),点E的位置随点P的位置变化而变化.
22. 在菱形中, , P是直线上一动点,以为边向右侧作等边(A,P,E按逆时针排列),点E的位置随点P的位置变化而变化. (1)、如图1,当点P在线段上,且点E在菱形内部或边上时,连接 , 则与的数量关系是 , 与的位置关系是;(2)、如图2,当点P在线段上,且点E在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)、当点P在直线上时,其他条件不变,连接 , 若 , , 请直接写出的面积.23. 如图,在菱形中, , 、分别为线段、上的两点.且 , , 相交于点
(1)、如图1,当点P在线段上,且点E在菱形内部或边上时,连接 , 则与的数量关系是 , 与的位置关系是;(2)、如图2,当点P在线段上,且点E在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)、当点P在直线上时,其他条件不变,连接 , 若 , , 请直接写出的面积.23. 如图,在菱形中, , 、分别为线段、上的两点.且 , , 相交于点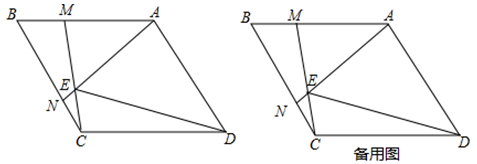 (1)、证明:≌;(2)、求的度数;(3)、证明: .24. 菱形的边长为 , , 点是对角线中点,是线段上任一点,连接 , 作 , 边与直线相交于点 .
(1)、证明:≌;(2)、求的度数;(3)、证明: .24. 菱形的边长为 , , 点是对角线中点,是线段上任一点,连接 , 作 , 边与直线相交于点 .
小南和小浦观察以上问题时,猜想 , 老师引导他们用“从特殊到一般”的思想方法去尝试研究.
(1)、【特例发现】
小南发现:当点与点重合时,与的长度相等,为;(2)、【探究证明】
小浦认为当在线段上时,均有“”,请帮助完成证明.(3)、【拓展运用】
①连结交于点 , 求证:为定值.②当时, ▲ .
25. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 . 26. 已知,菱形ABCD(∠C<90°)的对角线长分别为6和8,点E在边BC上,BE=1,若点F在直线AB上,且AE=DF,则BF的长为.
26. 已知,菱形ABCD(∠C<90°)的对角线长分别为6和8,点E在边BC上,BE=1,若点F在直线AB上,且AE=DF,则BF的长为. 27. 如图,四边形ABCD是菱形,点M在CD边上,点N在菱形ABCD外部,且满足MN∥AD,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC.
27. 如图,四边形ABCD是菱形,点M在CD边上,点N在菱形ABCD外部,且满足MN∥AD,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC.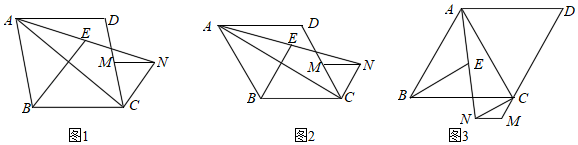 (1)、探究BE与AC的关系;(2)、若∠ABC=120°,探究线段BE、AD、CM所满足的等量关系;(3)、若∠ABC=60°,M在DC的延长线上时,其余条件不变,CM=1,AD=3,请求出BE的长度.28. 如图,菱形ABCD中,AB=12,∠BAD=60°,E为线段BC的中点.若点P是线段AB上的一动点,Q为线段AD上一动点,则 PQE的周长的最小值是.
(1)、探究BE与AC的关系;(2)、若∠ABC=120°,探究线段BE、AD、CM所满足的等量关系;(3)、若∠ABC=60°,M在DC的延长线上时,其余条件不变,CM=1,AD=3,请求出BE的长度.28. 如图,菱形ABCD中,AB=12,∠BAD=60°,E为线段BC的中点.若点P是线段AB上的一动点,Q为线段AD上一动点,则 PQE的周长的最小值是. 29. 如图,在菱形中, , E是对角线上一点,F是线段延长线上一点且 , 连接 .(1)、如图,若E是线段的中点,连接 , 其他条件不变,直接写出线段与的数量关系;
29. 如图,在菱形中, , E是对角线上一点,F是线段延长线上一点且 , 连接 .(1)、如图,若E是线段的中点,连接 , 其他条件不变,直接写出线段与的数量关系; (2)、如图,若E是线段上任意一点,连接 , 其他条件不变,猜想线段与的数量关系是什么?并证明你的猜想;
(2)、如图,若E是线段上任意一点,连接 , 其他条件不变,猜想线段与的数量关系是什么?并证明你的猜想; (3)、如图,若E是线段延长线上一点,其他条件不变,且 , 菱形的周长为 , 直接写出的长度.
(3)、如图,若E是线段延长线上一点,其他条件不变,且 , 菱形的周长为 , 直接写出的长度.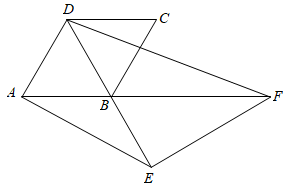 30. 如图,在▱ABCD中,对角线BD的垂直平分线分别与AD,BC,BD相交于点E,F,O.
30. 如图,在▱ABCD中,对角线BD的垂直平分线分别与AD,BC,BD相交于点E,F,O. (1)、求证:四边形BEDF是菱形;(2)、在▱ABCD中,若AB=2.5,AD=4,有两动点P,Q分别从B,D两点同时出发,沿△BAE和△DFC各边运动一周,即点P自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是x,点Q运动的路程是y,当四边形BPDQ是平行四边形时,则请直接写出x+y的值为 .
(1)、求证:四边形BEDF是菱形;(2)、在▱ABCD中,若AB=2.5,AD=4,有两动点P,Q分别从B,D两点同时出发,沿△BAE和△DFC各边运动一周,即点P自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是x,点Q运动的路程是y,当四边形BPDQ是平行四边形时,则请直接写出x+y的值为 .