人教版初中数学几何辅助线进阶训练——矩形的辅助线(不含相似)
试卷更新日期:2023-05-03 类型:复习试卷
一、阶段一(较易)
-
1. 如图,四边形是矩形,点是延长线一点,连接 , 垂直平分 , 垂足为 , 点在上,点在上,且.
 (1)、若 , , 求;(2)、若 , 求证:.2. 如图,在长方形ABCD中,AB=8,GC= , AE平分∠BAG交BC于点E,E是BC的中点,则AG的长为.
(1)、若 , , 求;(2)、若 , 求证:.2. 如图,在长方形ABCD中,AB=8,GC= , AE平分∠BAG交BC于点E,E是BC的中点,则AG的长为. 3. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( )
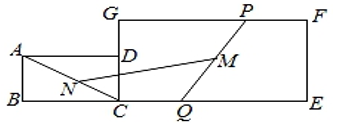
3. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( ) A、3 B、 C、 D、64. 如图,长方形ABCD中, , , , 点M是射线BD上一点(不与点B,D重合),连接AM,过点M作交直线BC于点N,若是等腰三角形,则 .
A、3 B、 C、 D、64. 如图,长方形ABCD中, , , , 点M是射线BD上一点(不与点B,D重合),连接AM,过点M作交直线BC于点N,若是等腰三角形,则 . 5. 如图,已知在△OAB中AO=BO,分别延长AO,BO到点C、D,使得OC=AO,OD=BO,连接AD,DC,CB.
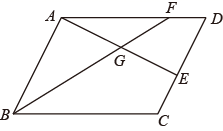
5. 如图,已知在△OAB中AO=BO,分别延长AO,BO到点C、D,使得OC=AO,OD=BO,连接AD,DC,CB. (1)、求证:四边形ABCD是矩形;(2)、以AO,BO为一组邻边作平行四边形AOBE,连接CE.若CE⊥AE,求∠AOB的度数.6. 如图,在中, , 为边上的中线,点E为AD的中点,作点B关于点E的对称点F,连接 , .
(1)、求证:四边形ABCD是矩形;(2)、以AO,BO为一组邻边作平行四边形AOBE,连接CE.若CE⊥AE,求∠AOB的度数.6. 如图,在中, , 为边上的中线,点E为AD的中点,作点B关于点E的对称点F,连接 , . (1)、求证:四边形为矩形;(2)、若 , , 求的长.7. 如图,△ABC中,AB=AC,AD为BC上的高线,E为AB边上一点,EF⊥BC于点F,交CA的延长线于点G. 已知EF=2,EG=3. 则AD的长为 .
(1)、求证:四边形为矩形;(2)、若 , , 求的长.7. 如图,△ABC中,AB=AC,AD为BC上的高线,E为AB边上一点,EF⊥BC于点F,交CA的延长线于点G. 已知EF=2,EG=3. 则AD的长为 . 8. 已知,在长方形ABCD中,AB=8,BC=6,点E,F分别是边AB,BC上的点,连接DE,DF,EF.
8. 已知,在长方形ABCD中,AB=8,BC=6,点E,F分别是边AB,BC上的点,连接DE,DF,EF. (1)、如图①,当CF=2BE=2时,试说明△DEF是直角三角形;(2)、如图②,若点E是边AB的中点,DE平分∠ADF,求BF的长.9. 如图,在矩形ABCD中,BC=4,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( )
(1)、如图①,当CF=2BE=2时,试说明△DEF是直角三角形;(2)、如图②,若点E是边AB的中点,DE平分∠ADF,求BF的长.9. 如图,在矩形ABCD中,BC=4,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( ) A、2 B、4 C、8 D、10. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( )
A、2 B、4 C、8 D、10. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、阶段二(一般)
-
11. 如图,将长方形纸片沿折叠后,点A,B分别落在 , 的位置,再沿边将折叠到处,已知 , 则 , .
 12. 如图,在矩形中,点E是对角线上一点,有且 , 点P是上一动点,则点P到边 , 的距离之和的值( )
12. 如图,在矩形中,点E是对角线上一点,有且 , 点P是上一动点,则点P到边 , 的距离之和的值( ) A、有最大值a B、有最小值 C、是定值 D、是定值13. 矩形与矩形如图放置,点、、共线,点、、共线,连接 , 取的中点 , 连接若 , , 则( )
A、有最大值a B、有最小值 C、是定值 D、是定值13. 矩形与矩形如图放置,点、、共线,点、、共线,连接 , 取的中点 , 连接若 , , 则( )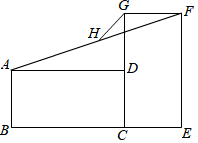 A、 B、 C、 D、14. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度
A、 B、 C、 D、14. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度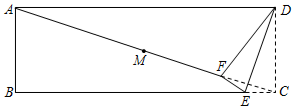 15. AM∥BN,ABBN,垂足为B, 点C在直线BN上,ACCD,AC=CD,DEAM,垂足为E.
15. AM∥BN,ABBN,垂足为B, 点C在直线BN上,ACCD,AC=CD,DEAM,垂足为E. (1)、如图①,求证:DE+BC=AB;(2)、如图②、图③,请分别写出线段DE,BC与AB之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,AC=100,AB-BC =2,则线段DE= .16. 如图,矩形ABCD中,交CD于点E,点F在AD上,连接CF交AE于点G, , 若 , 则CD的值为 .
(1)、如图①,求证:DE+BC=AB;(2)、如图②、图③,请分别写出线段DE,BC与AB之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,AC=100,AB-BC =2,则线段DE= .16. 如图,矩形ABCD中,交CD于点E,点F在AD上,连接CF交AE于点G, , 若 , 则CD的值为 . 17. 如图,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G、H分别是EC、FD的中点,连接GH,若AB=6,BC=10,则GH的长度为 .
17. 如图,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G、H分别是EC、FD的中点,连接GH,若AB=6,BC=10,则GH的长度为 . 18. 如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.
18. 如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF. (1)、若∠BAE=65°,∠DEC=40°,求∠ECD的度数;(2)、求证:四边形AFHD为平行四边形;(3)、连接EH,交BC于点O,若OC=OH,求证: .19. 如图,矩形 中, , 分别是边 , 的中点, 于 , 的延长线交 于 .下列结论:① ;② ;③ ;④ .其中结论正确的有( )
(1)、若∠BAE=65°,∠DEC=40°,求∠ECD的度数;(2)、求证:四边形AFHD为平行四边形;(3)、连接EH,交BC于点O,若OC=OH,求证: .19. 如图,矩形 中, , 分别是边 , 的中点, 于 , 的延长线交 于 .下列结论:① ;② ;③ ;④ .其中结论正确的有( )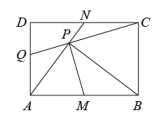 A、1个 B、2个 C、3个 D、4个20. 如图,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点H,G分别是EC,FD的中点,连接GH,若AB=6,BC=8,则GH的长度为( )
A、1个 B、2个 C、3个 D、4个20. 如图,在矩形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点H,G分别是EC,FD的中点,连接GH,若AB=6,BC=8,则GH的长度为( ) A、2 B、 C、 D、5
A、2 B、 C、 D、5三、阶段三(较难)
-
21. 如图,在矩形中,交于点 , 点在上,连接交于点 , 且 , 若 , 则的值是 ( )
 A、 B、 C、 D、822. 如图:在平面直角坐标系内有长方形 , 点A,C分别在y轴,x轴上,点在上,点E在上,沿折叠,使点B与点O重合,点C与点重合.若点P在坐标轴上,且面积是18,则点P坐标为 .
A、 B、 C、 D、822. 如图:在平面直角坐标系内有长方形 , 点A,C分别在y轴,x轴上,点在上,点E在上,沿折叠,使点B与点O重合,点C与点重合.若点P在坐标轴上,且面积是18,则点P坐标为 . 23. 阅读下列材料,完成相应任务.
23. 阅读下列材料,完成相应任务.直角三角形斜边上的中线等于斜边的一半
如图1,△ABC中, , BD是斜边AC上的中线.求证:BD=AC.
分析:要证明BD等于AC的一半,可以用“倍长法”将BD延长一倍,如图2.延长BD到E,使得DE=BD.
连接AE,CE.可证BE=AC,进而得到BD=AC.
 (1)、请你按材料中的分析写出证明过程;(2)、如图3,点C是线段AB上一点,CD⊥AB,点E是线段CD上一点,分别连接AD,BE,点F,G分别是AD和BE的中点,连接FG.若AB=12,CD=8,CE=3,则 .24. 如图,在长方形中, , . 点、点分别在、上,且 , 点是边上的动点,点是边上的动点.则的是小值是 .
(1)、请你按材料中的分析写出证明过程;(2)、如图3,点C是线段AB上一点,CD⊥AB,点E是线段CD上一点,分别连接AD,BE,点F,G分别是AD和BE的中点,连接FG.若AB=12,CD=8,CE=3,则 .24. 如图,在长方形中, , . 点、点分别在、上,且 , 点是边上的动点,点是边上的动点.则的是小值是 . 25. 在菱形ABCD中,∠BCD=60°,点P是直线AB上一点,且不与点A,点B重合,连接CP,作等边三角形PCE.
25. 在菱形ABCD中,∠BCD=60°,点P是直线AB上一点,且不与点A,点B重合,连接CP,作等边三角形PCE.
 (1)、如图1,若点P在线段AB上,连接DE,则线段PB,DE之间的数量关系是;(2)、如图2,若点P在线段AB的延长线上,连接AE,求证:EA=EP;(3)、如图3,若点P在线段BA的延长线上,顺次连接四边形ABCE各边的中点,则所得四边形的形状是 .26. 如图1,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为E.已知AD=4,BD=3.
(1)、如图1,若点P在线段AB上,连接DE,则线段PB,DE之间的数量关系是;(2)、如图2,若点P在线段AB的延长线上,连接AE,求证:EA=EP;(3)、如图3,若点P在线段BA的延长线上,顺次连接四边形ABCE各边的中点,则所得四边形的形状是 .26. 如图1,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为E.已知AD=4,BD=3. (1)、求证:四边形ADBE是矩形;(2)、如图2,延长AD至点F,使AF=AB,连接BF,G为BF的中点,连接EG,DG.求EG的长.(3)、如图3,在(2)问的条件下,P为BE边上的一个动点,连接PG并延长交AD延长线于点Q,连接CQ,H为CQ的中点,求点P从E点运动到B点时,点H所经过的路径长.27. 如图1,已知 , ,点D在 上,连接 并延长交 于点F,
(1)、求证:四边形ADBE是矩形;(2)、如图2,延长AD至点F,使AF=AB,连接BF,G为BF的中点,连接EG,DG.求EG的长.(3)、如图3,在(2)问的条件下,P为BE边上的一个动点,连接PG并延长交AD延长线于点Q,连接CQ,H为CQ的中点,求点P从E点运动到B点时,点H所经过的路径长.27. 如图1,已知 , ,点D在 上,连接 并延长交 于点F, (1)、猜想:线段 与 的数量关系为;(2)、探究:若将图1的 绕点B顺时针方向旋转,当 小于 时,得到图2,连接 并延长交 于点F,则(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由;(3)、拓展:图1中,过点E作 ,垂足为点G.当 的大小发生变化,其它条件不变时,若 , ,直接写出 的长.28. 将一块直角三角板的直角顶点和矩形ABCD(AB<BC)的对角线的交点O重合,如图(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
(1)、猜想:线段 与 的数量关系为;(2)、探究:若将图1的 绕点B顺时针方向旋转,当 小于 时,得到图2,连接 并延长交 于点F,则(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由;(3)、拓展:图1中,过点E作 ,垂足为点G.当 的大小发生变化,其它条件不变时,若 , ,直接写出 的长.28. 将一块直角三角板的直角顶点和矩形ABCD(AB<BC)的对角线的交点O重合,如图(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点. (1)、图①(三角板一直角边与OD重合)中,连接DN,则BN与DN的数量关系是 , 进而得到BN,CD,CN的数量关系是;(2)、写出图③(三角板一边与OC重合)中,CN,BN,CD的数量关系是;(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
(1)、图①(三角板一直角边与OD重合)中,连接DN,则BN与DN的数量关系是 , 进而得到BN,CD,CN的数量关系是;(2)、写出图③(三角板一边与OC重合)中,CN,BN,CD的数量关系是;(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.