初中数学同步训练必刷题（北师大版七年级下册 第六章 概率初步 全章测试卷）
试卷更新日期：2023-05-03 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 下列事件是随机事件的是（ ）A、打开电视，正在播放《中国机长》 B、白发三千丈，缘愁似个长 C、离离原上草，一岁一枯荣 D、钝角三角形的内角和大于2. 如图是一个游戏转盘，自由转动转盘，当转盘停止转动后，指针最大可能落在（ ）
A、红色区域 B、紫色区域 C、黄色区域 D、蓝色区域3. 按小王、小李、小马三位同学的顺序从一个不透明的盒子中随机抽取一张标注“主持人”和两张空白的纸条，确定一位同学主持班级“交通安全教有”主题班会.下列说法中正确的是（ ）A、小王的可能性最大 B、小李的可能性最大 C、小马的可能性最大 D、三人的可能性一样大4. 从甲，乙，丙三人中任选两名代表，甲被选中的可能性是（ ）A、 B、 C、 D、5. 小明任意抛掷一枚均匀骰子，六个面上分别刻着“1~6”的整数.抛掷一次正面朝上为偶数的概率为（ ）A、 B、 C、 D、6. 下列事件中，正确的是（ ）A、事件发生的可能性越大，概率越接近1 B、某种彩票中奖的概率是 ， 买100张该种彩票一定能中奖 C、抛掷一枚图钉，“针尖朝上”的概率是 D、射击运动员射击一次，命中靶心是必然事件7. 利用六张编号为1，2，3，4，5，6的扑克牌进行频率估计概率的试验中，同学小张统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（ ）
A、抽中的扑克牌编号是3的概率 B、抽中的扑克牌编号是3的倍数的概率 C、抽中的扑克牌编号大于3的概率 D、抽中的扑克牌编号是偶数的概率8. 在一个暗箱里放有个除颜色外完全相同的球，这个球中红球只有4个，每次将球充分摇匀后，随机从中摸出一球，记下颜色后放回，通过大量的重复试验后发现，摸到红球的频率为0.4，由此可以推算出约为（ ）A、7 B、3 C、10 D、69. 在一个不透明的口袋中装有2个红球和若干个白球，它们除颜色外其他完全相同.通过多次摸球试验后发现，摸到红球的频率稳定在20%附近，则口袋中白球可能有（ ）A、5个 B、6个 C、7个 D、8个10. 某小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图的折线统计图，则符合这一结果的试验最有可能的是（ ）
A、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率； B、任意写一个整数，它能被2整除的概率； C、掷一枚质地均匀正六面体骰子，向上的面点数是2的概率 D、暗箱中有1个红球和2个白球，它们只有颜色上的区别，从中任取一球是白球的概率二、填空题（每空3分，共30分）
-
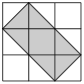
11. 抛掷一枚质地均匀的骰子一次，朝上一面的点数是2的倍数的概率是.12. 除夕的早上，小瑞和弟弟准备以掷骰子的方式决定谁来贴春联，由小瑞来投掷1个骰子，若掷出的点数不是3的倍数，则小瑞贴春联，否则弟弟贴春联，则小瑞贴春联的概率为 ．13. 在一个不透明的口袋中，装有若干个红球和7个黄球，它们只有颜色不同，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率稳定在0.7，则估计口袋中大约有红球 个．14. 如图，在方格纸中，随机撒一粒黄豆，落在阴影部分的概率是.
15. 淘宝某商户为了解新商品主图是否吸引人，对该商品的点击量和展现量进行了监测，得到商品点击率如下表所示：（注：）展现量
50
100
1000
5000
10000
50000
100000
点击量
4
7
78
385
760
3800
7600
点击率
根据上表，估计该商品展现量为30000时，点击率约为.
16. 某商场开展购物抽奖活动，抽奖箱内有标号分别为1、2、3、4、5、6、7、8、9、10十个质地、大小相同的小球，顾客从中任意摸出一个球，摸出的球的标号是3的倍数就得奖，顾客得奖概率是.17. 盒子里装有若干个彩色球，它们除颜色外完全相同，其中有6个黄球，从盒子中任意摸出一个球，摸到黄球的概率是 ， 则盒子里共有个彩色球．18. 如图是扫雷游戏的示意图.点击中间的按钮，若出现的数字是2，表明数字2周围的8个位置有2颗地雷，现任意点击这8个按钮中的一个，则不会出现地雷的概率为.
19. 圆周率是无限不循环小数.历史上，祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前，超级计算机已计算出的小数部分超过万亿位.有学者发现，随着小数部分位数的增加，这个数字出现的频率趋于稳定接近相同，从的小数部分随机取出一个数字，估计数字是的概率为.
20. 已知不透明的袋中装有红色、黄色、蓝色的乒乓球共120个，某学习小组做“用频率估计概率”的摸球试验（从中随机换出一个球，记下颜色后放回，统计了“摸出球为红色”出现的频率，绘制了如图的折线统计图，那么估计袋中红色球的数目为.（填整十数）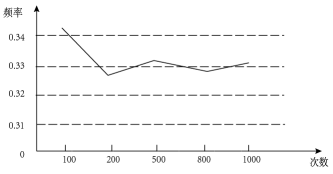
三、解答题（共5题，共60分）
-
21. 一只口袋里放着个红球、个黑球和若干个白球，这三种球除颜色外没有任何区别，并搅匀．(1)、取出红球的概率为 ， 白球有多少个？(2)、取出黑球的概率是多少？(3)、再在原来的袋中放进多少个红球，能使取出红球的概率达到？22. 如图，现有一个圆形转盘被平均分成6等份，分别标有2、3、4、5、6、7这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字．
(1)、转到数字9是 ， 转到数字6是 ， （从“随机事件”、“必然事件”、“不可能事件”选一个填入）(2)、转动转盘一次，转出的数字是3的倍数的概率是多少？(3)、现有两张分别写有2和5的卡片，随机转动转盘一次，转盘停止后记下转出的数字，与两张卡片上的数字分别作为三条线段的长度（长度单位均是厘米），这三条线段能构成三角形的概率是多少？23. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：摸球的次数n
1000
2000
3000
5000
8000
10000
摸到黑球的次数m
650
1180
1890
3100
4820
6013
摸到黑球的频率
0.65
0.59
0.63
0.62
0.6025
0.6013
(1)、请估计：当n很大时，摸到黑球的频率将会接近（精确到0.1）；(2)、试估计袋子中有黑球个；(3)、若学习小组通过试验结果，想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%，则可以在袋子中增加相同的白球个或减少黑球个．24. 某商场柜台为了吸引顾客，打出了一个小广告：本专柜为了感谢广大消费者的支持和厚爱，特举行购物抽奖活动，中奖率100%，最高奖50元．具体方法是：顾客每购买100元的商品，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准黄、红、绿、白色区域，顾客就可以分别获得50元、20元、10元、5元的购物券．（转盘的各个区域均被等分）请根据以上信息，解答下列问题：
(1)、小红的妈妈购物150元，她获得50元、5元购物券的概率分别是多少？(2)、请在转盘的适当地方写上一个区域的颜色，使得自由转动这个转盘，当它停止转动时，指针落在某一区域的事件发生概率为 ， 并说出此事件．25. 如图，某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：每购买500元商品，就能获得一次转动转盘的机会，如果转盘停止后，指针上对准的区域，顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份，如果指针恰好停在分割线上，那么重转一次，直到指针指向某一区域为止).
(1)、小华购物450元，他获得购物券的概率是多少?(2)、小丽购物600元，那么：①她获得50元购物券的概率是多少?
②她获得100元以上(包括100元)购物券的概率是多少?