初中数学同步训练必刷题(北师大版七年级下册 第五章 生活中的轴对称 全章测试卷)
试卷更新日期:2023-05-02 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,全面普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,若与关于直线对称,交于点 , 则下列说法中,不一定正确的是( )
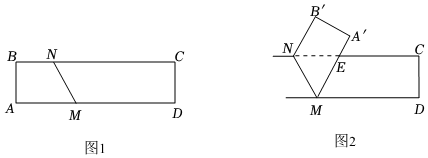
2. 如图,若与关于直线对称,交于点 , 则下列说法中,不一定正确的是( ) A、 B、 C、 D、3. 已知等腰三角形一腰上的中线将它的周长分成和两部分,则等腰三角形的底边长为( )A、 B、 C、或 D、或4. 如图,将沿AC所在的直线翻折得到 , 再将沿所在的直线翻折得到 , 点在同一条直线上, , 则( )
A、 B、 C、 D、3. 已知等腰三角形一腰上的中线将它的周长分成和两部分,则等腰三角形的底边长为( )A、 B、 C、或 D、或4. 如图,将沿AC所在的直线翻折得到 , 再将沿所在的直线翻折得到 , 点在同一条直线上, , 则( )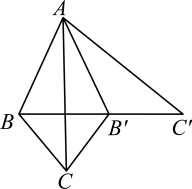 A、 B、 C、 D、5. 如图,在中, , 分别以点A、点B为圆心,大于的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若 , 则( )
A、 B、 C、 D、5. 如图,在中, , 分别以点A、点B为圆心,大于的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若 , 则( ) A、28° B、36° C、42° D、46°6. 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为10cm,则△ABC的周长为( )
A、28° B、36° C、42° D、46°6. 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为10cm,则△ABC的周长为( ) A、6cm B、10cm C、13cm D、16cm7. 如图,在△ABC中,∠C=90°,∠1=∠2,BC=16cm,点D到AB的距离为6cm,则BD的长为( )
A、6cm B、10cm C、13cm D、16cm7. 如图,在△ABC中,∠C=90°,∠1=∠2,BC=16cm,点D到AB的距离为6cm,则BD的长为( )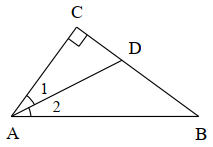 A、 B、 C、 D、8. 如图所示,将一张长方形纸片斜折过去,使顶点A落在处,BC为折痕,然后再把BE折过去,使之与重合,折痕为BD,若 , 则的度数为( )
A、 B、 C、 D、8. 如图所示,将一张长方形纸片斜折过去,使顶点A落在处,BC为折痕,然后再把BE折过去,使之与重合,折痕为BD,若 , 则的度数为( ) A、 B、 C、 D、9. 如图,在三角形纸片ABC中, . 将三角形纸片ABC沿DE折叠,使点A落在ABC所在平面内的点处.若 , 则的度数为( )
A、 B、 C、 D、9. 如图,在三角形纸片ABC中, . 将三角形纸片ABC沿DE折叠,使点A落在ABC所在平面内的点处.若 , 则的度数为( )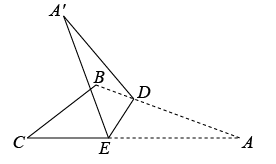 A、62.5° B、70° C、65° D、72.5°10. 如图(1)是一段长方形纸带, , 将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数为( )
A、62.5° B、70° C、65° D、72.5°10. 如图(1)是一段长方形纸带, , 将纸带沿折叠成图(2),再沿折叠成图(3),则图(3)中的的度数为( )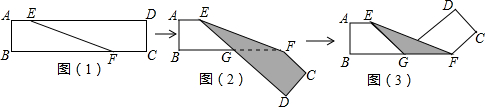 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共24分)
-
11. 等腰三角形的一边长为 , 另一边长为 , 则该等腰三角形的周长为 .12. 等腰三角形一腰上的高与另一腰的夹角为 , 则这个等腰三角形底角是 .13. 如图,OP平分∠MON,PA⊥ON于点A,若PA=3,则点P到射线OM的距离是 .
 14. 如图,在 的正方形网格中已有2个正方形涂黑,再选择一个正方形涂黑,使得3个涂黑的正方形组成轴对称图形,选择的位置共有处.
14. 如图,在 的正方形网格中已有2个正方形涂黑,再选择一个正方形涂黑,使得3个涂黑的正方形组成轴对称图形,选择的位置共有处. 15. 如图,在Rt△ABF中,∠AFB=90°,△CDE的顶点E在△ABF的边BF上,点C在BF的延长线上,∠C=∠B,且CD=CE,若∠A=36°,则∠D的度数为 .
15. 如图,在Rt△ABF中,∠AFB=90°,△CDE的顶点E在△ABF的边BF上,点C在BF的延长线上,∠C=∠B,且CD=CE,若∠A=36°,则∠D的度数为 . 16. 如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC面积为12,则BM+MD长度的最小值为 .
16. 如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC面积为12,则BM+MD长度的最小值为 . 17. 如图,在△ABC中,DF,EM分别垂直平分边AB,AC,若△AFM的周长为9,则BC= .
17. 如图,在△ABC中,DF,EM分别垂直平分边AB,AC,若△AFM的周长为9,则BC= .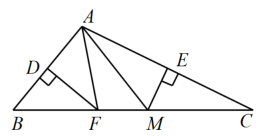 18. 如图,已知∠MON=30点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=1,则△A2021B2021A2022的边长为 .
18. 如图,已知∠MON=30点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=1,则△A2021B2021A2022的边长为 .
三、解答题(共6题,共66分)
-
19. 如图,在△ABC中,∠C=90°.
 (1)、用尺规作图法作∠CAB的平分线,交BC于点D(保留作图痕迹,不用写作法);(2)、在(1)的条件下,若CD=2,点E是AB边上的一个动点,连接DE,求DE的最小值.20. 如图,在中, , , , , 点D在边上,将沿折叠,使点A恰好落在边上的点处.
(1)、用尺规作图法作∠CAB的平分线,交BC于点D(保留作图痕迹,不用写作法);(2)、在(1)的条件下,若CD=2,点E是AB边上的一个动点,连接DE,求DE的最小值.20. 如图,在中, , , , , 点D在边上,将沿折叠,使点A恰好落在边上的点处. (1)、求的周长;(2)、若 , 求的度数.21. 如图,在△ABC中,AB=AC,作AB边的垂直平分线交直线BC于M,交AB于点N.
(1)、求的周长;(2)、若 , 求的度数.21. 如图,在△ABC中,AB=AC,作AB边的垂直平分线交直线BC于M,交AB于点N. (1)、如图(1),若∠A=40°,则∠NMB=度;(2)、如图(2),若∠A=70°,则∠NMB=度;(3)、如图(3),若∠A=120°,则∠NMB= 度;(4)、由(1)(2)(3)问,你能发现∠NMB与∠A有什么关系?写出猜想,并证明.22. 如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB对称点是D,连接CD交OA于M,交OB于N.
(1)、如图(1),若∠A=40°,则∠NMB=度;(2)、如图(2),若∠A=70°,则∠NMB=度;(3)、如图(3),若∠A=120°,则∠NMB= 度;(4)、由(1)(2)(3)问,你能发现∠NMB与∠A有什么关系?写出猜想,并证明.22. 如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB对称点是D,连接CD交OA于M,交OB于N. (1)、①若∠AOB=60°,则∠COD= ▲ °;
(1)、①若∠AOB=60°,则∠COD= ▲ °;②若∠AOB=α,求∠COD的度数.
(2)、若CD=4,则△PMN的周长为 .