初中数学同步训练必刷题（北师大版七年级下册 5.3 简单的轴对称图形）

试卷更新日期：2023-05-02 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 木工师傅将一把三角尺和一个重锤如图放置，就能检查一根横梁是否水平，能解释这一现象的数学知识是（）

A、角平分线定理 B、等腰三角形的三线合一 C、线段垂直平分线定理 D、两直线垂直的性质

查看试题解析
2. 等腰三角形的一个角是 $70 °$ ，则它的底角是（）

A、 $55 °$ B、 $70 °$ C、 $40 °$ 或 $70 °$ D、 $55 °$ 或 $70 °$

查看试题解析
3. 如图，△ABC中，AB＝6，BC＝4，AC的垂直平分线交AB，AC于点D和E，则△BCD的周长为（）

A、6 B、8 C、10 D、12

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B D$ 是 $△ A B C$ 的角平分线，过点 $D$ 作 $D E ⊥ A B$ ，垂足为 $E$ ，则下列结论错误的是（）

A、 $D E = D C$ B、 $∠ A D E = ∠ A B C$ C、 $B E = B C$ D、 $∠ A D E = ∠ A B D$

查看试题解析
5. 在 $△ A B C$ 中，分别以点A和B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧交于点M、N；作直线MN，交BC于点D；连接AD.若 $△ A D C$ 的周长为12， $A B = 6$ ，则 $△ A B C$ 的周长为（）

A、6 B、12 C、18 D、24

查看试题解析
6. 如图，在△ABC中，∠ABC=50°，∠ACB=100°，点M是射线AB上的一个动点，过点M作MN∥BC交射线AC于点N，连结BN。若△BMN中有两个角相等，则∠MNB的度数不可能是（）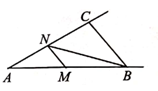

A、25° B、30° C、50° D、65°

查看试题解析
7. 如图，在 $△ A B C$ 中，DM垂直平分AB交AB于点D，交BC于点M，EN垂直平分AC交AC于点E．交BC于点N，且点M在点N的左侧，连AM，AN，若 $B C = 12 c m$ ，则 $△ A M N$ 的周长是（）

A、10cm B、12cm C、14cm D、16cm

查看试题解析
8. 如图，在△ABC中，AB＝AC，按如下步骤作图：以点A为圆心、适当长度为半径作弧，分别交AB、AC于点M、N；分别以点M、N为圆心、大于 $\frac{1}{2}$ MN的长为半径作弧，两弧相交于点F，连接AF并延长，交BC于点E．下列结论不一定成立的是（）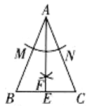

A、∠ABC＝∠ACB B、BE＝CE C、AE⊥BC D、∠BAE＝ $\frac{1}{2}$ ∠B

查看试题解析
9. 如图，由边长为1的小等边三角形构成的网格图中，有3个小等边三角形已涂上阴影．在余下的空白小等边三角形中选取一个涂上阴影，使得4个阴影等边三角形组成一个轴对称图形，符合选取条件的空白小等边三角形有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 已知等腰三角形一腰上的中线将这个等腰三角形的周长分为9cm和15cm两部分，则这个等腰三角形的腰长为（）

A、6cm B、10cm C、6cm或10cm D、11cm

查看试题解析

二、填空题（每空3分，共18分）

11. 等腰三角形的两边长分别为5和11，则这个三角形的周长为 .

查看试题解析
12. 如图，BO平分 $∠ A B C ， O D ⊥ B C$ 于点D，点E为射线BA上一动点，若 $O D = 5$ ，则OE的最小值为.

查看试题解析
13. 如图，在 $△ A B C$ 中，按以下步骤作图：①分别以点 $A$ 和 $B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于点 $M$ 和 $N$ ；②作直线 $M N$ ，分别交 $A B$ ， $A C$ 于点 $D$ ， $E$ ，连接 $B E$ ．若 $A C = 8$ ， $B C = 5$ ，则 $△ B C E$ 的周长为．

查看试题解析
14. 如图，在△ABC中，AB=AC，∠BAC=76°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数为.

查看试题解析
15. 如图，在锐角△ABC中，∠ABC＝30°，AC＝3，△ABC的面积为8，P为△ABC内部一点，分别作点P关于AB，BC，AC的对称点P₁ ， P₂ ， P₃ ，连接P₁P₂ ， PP₃ ，则2P₁P₂+PP₃的最小值为．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ C = 84 °$ ，分别以点 $A$ ， $B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧分别交于点 $M$ ， $N$ （点 $M$ 在 $A B$ 上方），作直线 $M N$ 交 $A C$ 边于点 $D$ ；在 $B A$ 和 $B C$ 上分别截取 $B E$ ， $B F$ ，使 $B E = B F$ ，分别以点 $E$ ， $F$ 为圆心，以大于 $\frac{1}{2} E F$ 的长为半径作弧，两弧在 $∠ A B C$ 内交于点 $P$ ，作射线 $B P$ ，若射线 $B P$ 恰好经过点 $D$ ，则 $∠ A =$ $°$ ．

查看试题解析

三、解答题（共8题，共72分）

17. 如图，等腰 $△ A B C$ 中， $A B = A C$ ， $∠ B = 35 °$ ， $E$ 是 $B C$ 边上一点且 $A E = C E$ ， $D$ 是 $B C$ 边上的中点，连接 $A D$ ， $A E$ ．

(1)、求 $∠ D A E$ 的度数；

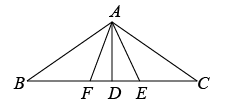(2)、若 $B D$ 上存在点 $F$ ，连接 $A F$ ，且 $∠ A F E = ∠ A E F$ ，试判断 $B F$ 与 $C E$ 之间的数量关系，并说明理由．

查看试题解析
18. 如图，在△ABC中，∠ABC＝20°，∠ACB＝65°，DE，FG分别为AB，AC的垂直平分线，E，G分别为垂足．

(1)、求∠DAF的度数．

(2)、若BC的长为50，求△DAF的周长．

查看试题解析
19. 尺规作图是理论上接近完美的作图方式，乐乐很喜欢用尺规画出要求的图形.在下面的 $△ A B C$ 中，请你也按要求用尺规作出下列图形（不写作法，但要保留作图痕迹）并填空.

（ 1 ）作出 $∠ B A C$ 的平分线交 $B C$ 边于点 $D$ ；

（ 2 ）作出 $A C$ 边上的垂直平分线 $l$ 交 $A D$ 于点 $G$ ；

（ 3 ）连接 $G C$ ，若 $∠ B = 55 ° ， ∠ B C A = 60 °$ ，则 $∠ A G C$ 的度数为▲ .

查看试题解析
20. 已知 $O M$ 是 $∠ A O B$ 的平分线，点 $P$ 是射线 $O M$ 上点，点 $C$ ， $D$ 分别在射线 $O A$ ， $O B$ 上，连接 $P C$ ， $P D$ .

(1)、发现问题：如图1，当 $P C ⊥ O A$ ， $P D ⊥ O B$ 时，则 $P C$ 与 $P D$ 的数量关系是.

(2)、探究问题：如图2，点 $C$ ， $D$ 在射线 $O A$ ， $O B$ 上滑动，且 $∠ A O B = 90 °$ ，当 $P C ⊥ P D$ 时， $P C$ 与 $P D$ 在（1）中的数量关系还成立吗？说明理由.（温馨提示：过 $P$ 作 $P E ⊥ O A$ 于 $E$ ， $P F ⊥ O B$ 于 $F$ ）

查看试题解析
21. 如图， $△ A B C$ 和 $△ B D E$ 均为等边三角形，点 $A$ ， $B$ ， $E$ 在同一直线上，且点 $C$ ， $D$ 在 $A E$ 所在直线的同一侧，连接 $A D$ ， $C E$ ， $A D$ 与 $C E$ 相交于点 $F$ ， $A D$ 与 $B C$ 相交于点 $G$ ．

(1)、 $△ A B D$ 与 $△ C B E$ 全等吗？请说明理由；

(2)、求 $∠ A F C$ 的度数．

查看试题解析
22. 数学理解

(1)、如图1，在等边 $△ A B C$ 内，作 $D B = D C$ ，且 $∠ B D C = 80 °$ ， E是 $△ D B C$ 内一点，且 $∠ C B E = 10 °$ ， $B E = B D$ ，求 $∠ B C E$ 的度数；

(2)、如图2，在 $△ D B C$ 中， $D B = D C$ ， $∠ B D C = 80 °$ ， E是 $△ D B C$ 内一点，且 $∠ C B E = 10 °$ ， $∠ B C E = 30 °$ ，连接DE，求 $∠ C D E$ 的度数．

查看试题解析
23. 如图，直线l与a、b相交于点A、B，且 $a ∥ b$ ．

(1)、尺规作图：过点B作 $∠ A B C$ 的角平分线交直线a于点D（保留作图痕迹，标注有关字母，不用写作法和证明）；

(2)、若 $∠ 1 = 48 °$ ，求 $∠ A D B$ 的度数；

(3)、P为直线l上任意一点，若点D到直线b的距离为 $3 c m$ ，则DP的最小值为cm．

查看试题解析
24. 如图，△ABC中∠ACB＝90°，将△ABC沿着一条直线折叠后，使点A与点C重合（如图②）．

(1)、在图①中用尺规作出折痕所在的直线l ，保留作图痕迹（不用写作法）；

(2)、直线l是线段AC的线；

(3)、设直线l与AB、AC分别相交于点M、N ，连接CM ，若△CMB的周长是21cm，AB＝14cm，求BC的长．

查看试题解析