2023年苏科版数学七年级下册全方位训练卷第十二章 证明
试卷更新日期:2023-05-02 类型:单元试卷
一、单选题(每题3分,共24分)
-
1. 下列语句中,不是命题的是( )A、两点确定一条直线 B、同位角相等 C、垂线段最短 D、连接、两点2. 对于命题“如果 , 那么 , 下面四组关于的值中,能说明这个命题是假命题的是( )A、 B、 C、 D、3. 下列命题是真命题的是( )A、相等的角是对顶角 B、在同一平面内,垂直于同一直线的两条直线平行 C、内错角相等 D、如果两个角的和等于平角,那么这两个角是邻补角4. 下列定理中没有逆定理的是( )A、内错角相等,两直线平行 B、直角三角形中,两锐角互余 C、等腰三角形两底角相等 D、对顶角相等5. 下列说法正确的是( )A、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 B、等腰三角形的高、中线、角平分线互相重合 C、“长度为3cm,4cm,5cm的三条线段可以构成三角形”是必然事件 D、“400人中有两人生日在同一天”是随机事件6. 命题“如果a<0,b<0,那么ab>0”的逆命题是( )A、如果a<0,b<o,那么ab<0 B、如果ab>0,那么a<0,b<0 C、如果a>0,b>0,那么a<0 D、如果ab<0,那么a>0,b>07. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:
证明:如图,∵ , ∴∠1=90°.
∵ , ∴∠2=90°,
∴∠1=∠2,∴ .
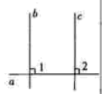
已知该证明过程是正确的,则证明的真命题是( )
A、在同一平面内,若 , 且 , 则 B、在同一平面内,若 , 且 , 则 C、同位角相等,两直线平行 D、两直线平行,同位角相等8. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.
求证:∠ACD=∠A+∠B.
证法1:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理)
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质)
证法2:如图,
∵∠A=88°,∠B=58°,
且∠ACD=146°(量角器测量所得)
又∵146°=88°+58°(计算所得)
∴∠ACD=∠A+∠B(等量代换)
下列说法正确的是( )
 A、证法1还需证明其他形状的三角形,该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证,就能证明该定理
A、证法1还需证明其他形状的三角形,该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证,就能证明该定理二、填空题(每空3分,共24分)
-
9. 将命题:“相交的两条直线一定不平行”改写成“如果……那么……”的形式: .10. 命题“如果一个三角形的两个角互余,那么这个三角形是直角三角形”的逆命题是: .11. 请写出命题“如果 ,那么 ”的逆命题:.12. 命题“平行于同一条直线的两条直线平行”的题设是 , 结论是这两条直线平行。13. 下列说法正确的是(填序号)
①三角形的三条角平分线相交于一点 ②三角形的三条高相交于一点
③全等三角形的面积相等 ④面积相等的三角形全等
14. 下列命题中:①两点的所有连线中,线段最短;②不等式两边加同一个数,不等号的方向改变;③等式两边加同一个数,结果仍相等;④两条直线被第三条直线所截,同位角相等.是假命题的是:(填编号)15. “如果 , 那么”的逆命题是.16. 命题:“若m=n,则”的逆命题为.三、解答题(共8题,共72分)
-
17. 写出下列命题的逆命题:(1)、两条直线被第三条直线所截,如果有一对同位角相等,那么这两条直线平行;(2)、角平分线上的点到角的两边的距离相等;(3)、若r²=a,则r叫a的平方根;(4)、如果a≥0,那么 =a.18. 证明是13的倍数.19. 完成下列证明:
如图,已知于点 , 于点 , 于点 , ,

求证: .
证明: , 已知 ,
▲ ,
▲ 两直线平行,内错角相等 ,
, 已知 ,
_▲ ,
,
已知 ,
.
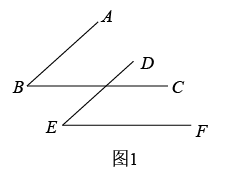
20. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性. 21. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
21. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.已知: ▲ . 结论: ▲ .
理由:
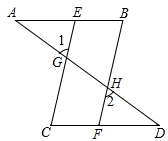 22. 如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
22. 如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题. (1)、你构造的是哪几个命题?(2)、你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
(1)、你构造的是哪几个命题?(2)、你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).