2023年苏科版数学七年级下册全方位训练卷 12.2 证明
试卷更新日期:2023-05-01 类型:同步测试
一、单选题(每题3分,共21分)
-
1. 如图,不能推出的条件是( )
 A、 B、 C、 D、2. 如图所示,不能证明ABCD的是( )
A、 B、 C、 D、2. 如图所示,不能证明ABCD的是( )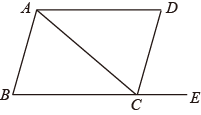 A、∠BAC=∠ACD B、∠ABC=∠DCE C、∠DAC=∠BCA D、∠ABC+∠DCB=180°3. 下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )A、
A、∠BAC=∠ACD B、∠ABC=∠DCE C、∠DAC=∠BCA D、∠ABC+∠DCB=180°3. 下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )A、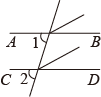 B、
B、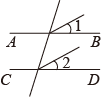 C、
C、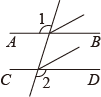 D、
D、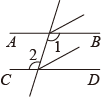 4. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:
4. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:证明:如图,∵ , ∴∠1=90°.
∵ , ∴∠2=90°,
∴∠1=∠2,∴ .
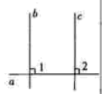
已知该证明过程是正确的,则证明的真命题是( )
A、在同一平面内,若 , 且 , 则 B、在同一平面内,若 , 且 , 则 C、同位角相等,两直线平行 D、两直线平行,同位角相等5. 如图,在中,点D为边上一点,给出如下关系:①平分;②于D;③D为中点.甲说:如果①②同时成立,可证明;乙说:如果②③同时成立,可证明;丙说:如果①③同时成立,可证明.则正确的说法是( ) A、甲、乙正确,丙错误 B、甲正确,乙、丙错误 C、乙正确,甲、丙错误 D、甲、乙、丙都正确6. 定理:三角形的内角和等于180°.
A、甲、乙正确,丙错误 B、甲正确,乙、丙错误 C、乙正确,甲、丙错误 D、甲、乙、丙都正确6. 定理:三角形的内角和等于180°.已知:的三个内角为、、
求证: .
证法1:如图
∵ , , (量角器测量)
∵(计算所得)
∴(等量代换)

证法2:如图,延长到 , 过点作 .
∴(两直线平行,内错角相等)
(两直线平行,同位角相等)
∵(平角定义).
∴(等量代换)
即 .

下列说法正确的是( )
A、证法1采用了从特殊到一般的方法证明了该定理 B、证法1还需要测量一百个进行验证,就能证明该定理 C、证法2还需证明其它形状的三角形,该定理的证明过程才完整 D、证法2用严谨的推理证明了该定理7. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.证法1:如图,
∵∠A=70°,∠B=63°,
且∠ACD=133°(量角器测量所得)
又∵133°=70°+63°(计算所得)
∴∠ACD=∠A+∠B(等量代换).
证法2:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理),
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质).
下列说法正确的是( )
 A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证,就能证明该定理 C、证法2还需证明其他形状的三角形,该定理的证明才完整 D、证法2用严谨的推理证明了该定理
A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证,就能证明该定理 C、证法2还需证明其他形状的三角形,该定理的证明才完整 D、证法2用严谨的推理证明了该定理二、解答题
-
8. 证明:等腰三角形的两底角相等9. 完成下面的证明.
如图、与互补, , 求证:.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
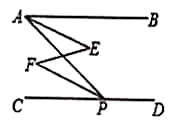
证明:与互补,(已知)
.( )
.( )
, (已知)
, (等量代换)
即_▲_=_▲_.
.( )
.( )
10. 完成下面的证明过程:已知:如图, , , , 求证:.

证明:∵ , (已知),
∴ ,
∴ ▲ ( ).
又∵(已知),
∴ ▲ ,
∴ ▲ ( ).
∴( ).
11. 已知:如图.求证:平分.
请完善证明过程,并在括号内填上相应依据:
证明:
∵ , ( )
∴ ▲ ▲ , ( )
∴ , ( )
∴ , ( )
∵(已知),
∴ ▲ ▲ , ( )
∴平分.( )
12. 叙述并证明三角形内角和定理.13. 如图, , 的平分线交于点F,交的延长线于点E, , 求证:.
请将下面的证明过程补充完整:
证明:∵(已知),
∴ , (① )
∵平分 ,
∴②▲ .(③ )
∴.(④ )
∵(已知),
∴⑤▲ .(⑥ )
∴.(⑦ )
∴.(⑧ )
14. 阅读下面的解答过程,并填空.如图, , 平分 , 平分 , . 求证: .

证明:∵平分 , 平分 , (已知)
∴ ▲ , ▲ . (角平分线的定义)
又∵ , (已知)
∴∠ ▲ =∠ ▲ . (等量代换)
又∵ , (已知)
∴∠ ▲ ∠ ▲ . (等量代换)
∴ . ( )
15. 证明命题“三角形三个内角的和等于180°”是真命题.已知:
求证:
证明:
16. 下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明. 三角形内角和定理:三角形三个内角和等于180°,
三角形内角和定理:三角形三个内角和等于180°,已知:如图, ,
求证:
方法一
证明:如图,过点A作

方法二
证明:如图,过点C作
