2022-2023学年人教版七年级数学下期末复习 相交线平行线
试卷更新日期:2023-05-01 类型:复习试卷
一、单选题
-
1. 如图各图中,∠1与∠2是对顶角的是( )A、
 B、
B、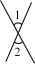 C、
C、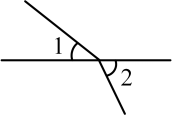 D、
D、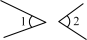 2. 2023 年第十九届亚运动会在中国杭州举办,其中吉祥物“莲莲”深受大家喜爱.由下图平移得到的图形是( )
2. 2023 年第十九届亚运动会在中国杭州举办,其中吉祥物“莲莲”深受大家喜爱.由下图平移得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,是测量学生跳远成绩的示意图,即的长为某同学的跳远成绩,其依据是( )
3. 如图,是测量学生跳远成绩的示意图,即的长为某同学的跳远成绩,其依据是( ) A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过一点有且只有一条直线与已知直线垂直4. 如图所示,∠1和∠2是同位角的是( )
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过一点有且只有一条直线与已知直线垂直4. 如图所示,∠1和∠2是同位角的是( ) A、②③ B、①②③ C、①②④ D、①④5. 如图,直线和相交于点O,平分 , .若 , , 则以下等式一定成立的是( )
A、②③ B、①②③ C、①②④ D、①④5. 如图,直线和相交于点O,平分 , .若 , , 则以下等式一定成立的是( )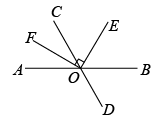 A、 B、 C、 D、6. 如图所示,以下5个条件:①∠B=∠4+∠5;②∠2=∠4;③∠1=∠5;④∠B=∠3;⑤∠D+∠4+∠5= 180°.其中一定能判定AD∥BC的有( )
A、 B、 C、 D、6. 如图所示,以下5个条件:①∠B=∠4+∠5;②∠2=∠4;③∠1=∠5;④∠B=∠3;⑤∠D+∠4+∠5= 180°.其中一定能判定AD∥BC的有( ) A、4个 B、3个 C、2个 D、1个7. 能说明命题“对于任何实数a,都有|a|=a"是假命题的反例是( )A、a=-2 B、a= C、a=1 D、a=8. 如图, , , 则、和的关系是( )
A、4个 B、3个 C、2个 D、1个7. 能说明命题“对于任何实数a,都有|a|=a"是假命题的反例是( )A、a=-2 B、a= C、a=1 D、a=8. 如图, , , 则、和的关系是( ) A、 B、 C、 D、9. 如图,三角板的直角顶点在直尺的一边上.若∠1=30°,∠2=70°,则∠3的度数是( )
A、 B、 C、 D、9. 如图,三角板的直角顶点在直尺的一边上.若∠1=30°,∠2=70°,则∠3的度数是( ) A、30° B、40° C、50° D、60°10. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )
A、30° B、40° C、50° D、60°10. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )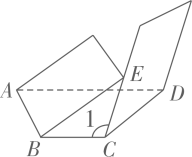 A、106° B、108° C、109° D、110°
A、106° B、108° C、109° D、110°二、填空题
-
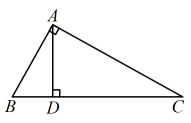
11. 如图: , , 垂足分别为A、D,则图中线段的长度能表示点到直线的距离的共有条.
 12. 如图是对顶角量角器,它所测量的角是度.
12. 如图是对顶角量角器,它所测量的角是度. 13. 如图,是的平分线, , , 则.
13. 如图,是的平分线, , , 则. 14. 如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=100°,∠B=160°,则∠C的度数是 .
14. 如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=100°,∠B=160°,则∠C的度数是 . 15. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时, , 则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为.
15. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时, , 则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为.
三、解答题
-
16. 如图,∠ABC+∠ECB=180°,∠P=∠Q.
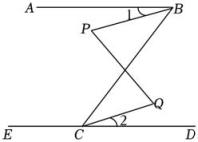
求证:∠1=∠2.
根据图形和已知条件,请补全下面这道题的解答过程.
证明:∵∠ABC+∠ECB=180°( ),
∴AB∥ED( ).
∴∠ABC=∠BCD( ).
又∵∠P=∠Q(已知),
∴PB∥ ▲ .
∴∠PBC= ▲ .
又∵∠1=∠ABC- ▲ , ∠2=∠BCD- ▲ ,
∴∠1=∠2(等量代换).
17. 如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2. 18. 如图,和相交于点 , 平分 , 于点 , , 求的度数.
18. 如图,和相交于点 , 平分 , 于点 , , 求的度数. 19. 如图,在四边形中, , , 平分 , 平分 , 则与有何位置关系?试说明理由.
19. 如图,在四边形中, , , 平分 , 平分 , 则与有何位置关系?试说明理由.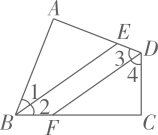 20. 如图,将△ABC向左平移6个单位长度,再向下平移4个单位长度,可以得到△A1B1C1 , 画出平移后的△A1B1C1
20. 如图,将△ABC向左平移6个单位长度,再向下平移4个单位长度,可以得到△A1B1C1 , 画出平移后的△A1B1C1
①直接写出△A1B1C1各个顶点的坐标;
②写出S△ABC= ▲ .
21. 如图,有三个论断①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.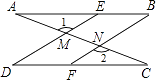
四、综合题
-
22. 如图,已知 , , 点是射线上一动点(与点不重合), , 分别平分和 , 交射线于点 , .
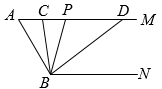 (1)、求的度数;(2)、在点运动过程中,试判断与之间的数量关系?并说明理由;(3)、当点运动到使时,求出的度数.23. 如图1,点O在直线上,过点O引一条射线 , 使 , 将一个直角三角尺的直角顶点放在点O处,直角边在射线上,另一边在直线的下方.
(1)、求的度数;(2)、在点运动过程中,试判断与之间的数量关系?并说明理由;(3)、当点运动到使时,求出的度数.23. 如图1,点O在直线上,过点O引一条射线 , 使 , 将一个直角三角尺的直角顶点放在点O处,直角边在射线上,另一边在直线的下方.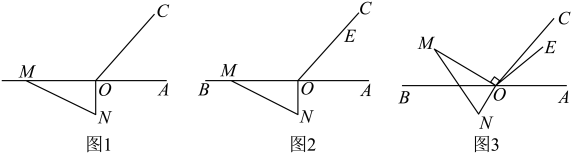
【操作一】:将图1中的三角尺绕着点O以每秒的速度按顺时针方向旋转.当它完成旋转一周时停止,设旋转的时间为t秒.
(1)、的度数是 , 图1中与它互补的角是.(2)、三角尺旋转的度数可表示为(用含t的代数式表示);当时,.(3)、【操作二】:如图2将一把直尺的一端点也放在点O处,另一端点E在射线上.如图3,在三角尺绕着点O以每秒的速度按顺时针方向旋转的同时,直尺也绕着点O以每秒的速度按顺时针方向旋转,当一方完成旋转一周时停止,另一方也停止旋转,设旋转的时间为t秒. 试探索:在三角尺与直尺旋转的过程中,当 , 是否存在某个时刻,使得与中其中一个角是另一个角的两倍?若存在,请求出所有满足题意的t的值;若不存在,请说明理由.