2023年浙江省杭州市初中毕业生学业水平测试数学模拟试题(四)

试卷更新日期：2023-04-30 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 有理数 $- \frac{1}{2}$ ， 5，0， $- (- 3)$ ， $- 2$ ， $- | - 25 |$ 中，负数的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
2. “水是生命之源，滋润着世间万物"国家节水标志由水滴，手掌和地球变形而成．寓意：像对待掌上明珠一样，珍惜每一滴水！以下通过平移左侧的节水标志得到的图形是（）

A、 B、 C、 D、

查看试题解析
3. 用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为( )

A、2πcm B、1.5cm C、πcm D、1cm

查看试题解析
4. 下列说法正确的是（）

A、要了解一批灯泡的使用寿命，采用全面调查的方式 B、要了解全市居民对环境的保护意识，采用抽样调查的方式 C、一个游戏的中奖率是1%，则做100次这这样的游戏一定会中奖 D、若甲组数据的方差S_甲²=0.05，乙组数据的方差S_乙²=0.1，则乙组数据比甲组数据稳定

查看试题解析
5. 如图所示的物体有两个紧靠在一起的圆柱体组成，它的主视图是（）

A、 B、 C、 D、

查看试题解析
6. 北斗卫星导航系统是中国自行研制的全球卫星导航系统，授时精度优于0.00000001秒，0.00000001用科学记数法可表示为（）

A、0.1×10^﹣7 B、1×10^﹣8 C、1×10^﹣7 D、0.1×10^﹣8

查看试题解析
7. 在矩形纸片 $A B C D$ 中， $A B = 2 c m$ ， $B C = 4 c m$ ，现将纸片折叠压平，使 $A$ 与 $C$ 重合，如果设折痕为 $E F$ ，那么重叠部分 $△ A E F$ 的面积等于（）

A、1 B、1.5 C、2 D、2.5

查看试题解析
8. 如图，线段AB= $\sqrt{2}$ 、CD= $\sqrt{5}$ ，那么，线段EF的长度为（）

A、 $\sqrt{7}$ B、 $\sqrt{11}$ C、 $\sqrt{13}$ D、 $\sqrt{15}$

查看试题解析
9. 已知抛物线 $y = a x^{2} + b x + c$ 的部分图象如图所示，则当y>0时，x的取值范围是（）

A、x<3 B、x>-1 C、-1<x<3 D、x<-1或x>3

查看试题解析
10. 如图，半径为A的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F，当点E从点B出发逆时针运动到点C时，点F经过的路径长是（）

A、 $\frac{4 π}{3}$ B、 $\frac{8 \sqrt{3} π}{3}$ C、 $\frac{4 \sqrt{3} π}{3}$ D、2 $\sqrt{3}$ π

查看试题解析

二、填空题（每空4分，共24分）

11. 当x时，式子 $x + 2$ 的值不小于 $2 x - 1$ 的值

查看试题解析
12. 若M＝a²-ac+1，N＝ac-c² ，则M与N的大小关系是MN．

查看试题解析
13. 在一个不透明的袋子中，装有2个红球和3个白球，它们除颜色外其余均相同．现随机从袋中摸出一个球，颜色是白色的概率是．

查看试题解析
14. 如图，圆 $O$ 过正方形 $A B C D$ 的顶点 $A$ 、 $D$ ，且与边 $B C$ 相切，若正方形的边长为 $2$ ，则圆 $O$ 的半径为．

查看试题解析
15. 如图，在 $Δ A B C$ 中， $∠ C = 90^{°} ， A C = B C ， A B = 2 \sqrt{2} + 2$ ，点M，N分别是AB，AC上的动点，沿MN所在的直线折叠，使点A的对应点 $A^{'}$ 始终落在BC上， $Δ M A^{'} B$ 若为直角三角形，则BM的长为；

查看试题解析
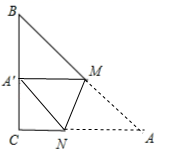16. 如图，二次函数y＝ax²+bx+c的图象开口向上，图象经过点（﹣1，2）和（1，0），且与y轴交于负半轴，给出六个结论：①a＞0；②b＞0；③c＞0；④a+b+c＝0；⑤b²﹣4ac＞0；⑥2a﹣b＞0，其中正确结论的序号是

查看试题解析

三、解答题（共7题，共66分）

17. 计算： ${(\frac{1}{2})}^{- 1} - 2 \cos 30 ° - {(2019 + π)}^{0} + 2 \sqrt{3} \sin 30 °$ .

查看试题解析
18.
某中学开展“绿化家乡、植树造林”活动，为了解全校植树情况，对该校甲、乙、丙、丁四个班级植树情况进行了调查，将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图，请根据图中的信息，完成下列问题：
（1）这四个班共植树多少棵？
（2）请你在答题卡上不全两幅统计图；
（3）求图1中“甲”班级所对应的扇形圆心角的度数；
（4）若四个班级植树的平均成活率是95%，全校共植树2000棵，请你估计全校种植的树中成活的树有多少棵？

查看试题解析
19. 如图，一座古塔AH的高为33米，AH⊥直线l ，某校九年级数学兴趣小组为了测得该古塔塔刹AB的高，在直线l上选取了点D ，在D处测得点A的仰角为26.6°，测得点B的仰角为22.8°，求该古塔塔刹AB的高．（精确到0.1米）(参考数据：sin26.6°＝0.45，cos26.6°＝0.89，tan26.6°＝0.5，sin22.8°＝0.39，cos22.8°＝092，tan22.8°＝0.42)

查看试题解析
20. 如图，图中的小方格都是边长为1的正方形，
①直接写出△ABC的各顶点坐标：
A（，），B （，），C （，）；
②画出△ABC关于y轴的对称图形△A₁B₁C₁；
③直接写出△ABC关于x轴对称的△A₂B₂C₂的顶点A₂ （，） B₂ （，） (其中A₂与A对应，B₂与B对应，不必画图．)

查看试题解析
21.
如图，点A、B在⊙O上，直线AC是⊙O的切线，OC⊥OB，连接AB交OC于点D．
（1）AC与CD相等吗？为什么？
（2）若AC=2，AO= $\sqrt{5}$ ，求OD的长度．

查看试题解析
22.
如图，已知△ABC中，AB=AC，D为△ABC所在平面内的一点，过D作DE∥AB，DF∥AC分别交直线AC、直线AB于点E、F．

（1）如图1，当点D在线段BC上时，通过观察分析线段DE、DF、AB之间的数量关系，并说明理由；
（2）如图2，当点D在直线BC上，其它条件不变时，试猜想线段DE、DF、AB之间的数量关系（请直接写出等式，不需证明）；
（3）如图3，当点D是△ABC内一点，过D作DE∥AB，DF∥AC分别交直线AC、直线AB和直线BC于E、F和G．试猜想线段DE、DF、DG与AB之间的数量关系（请直接写出等式，不需证明）．

查看试题解析
23. 如图1，正方形ABCD的边长为4，点E，F分别在BC，BD上，且BE=1，过三点C，E，F作⊙O交CD于点G。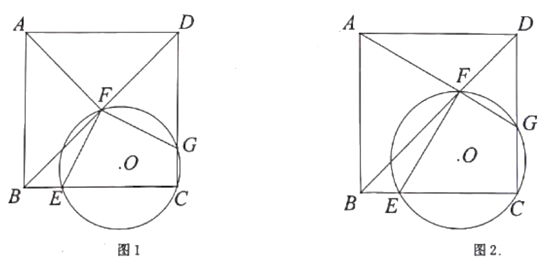

(1)、证明∠EFG=90°．

(2)、如图2，连结AF，当点F运动至点A，F，G三点共线时，求△ADF的面积。

(3)、在点F整个运动过程中，
①当EF，FG，CG中满足某两条线段相等，求所有满足条件的BF的长。

②连接EG，若 $\frac{E F}{F G} = \frac{1}{2}$ 时，求⊙O的半径(请直接写出答案)。

查看试题解析