2023年浙江省杭州市初中毕业生学业水平测试数学模拟试题(三)
试卷更新日期:2023-04-30 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 下列说法中,正确的是( )A、不带根号的数不是无理数 B、 的立方根是±2 C、绝对值等于 的实数是 D、每个实数都对应数轴上一个点2. 下列手机手势解锁图案中,是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 3. 一个空间几何体的主视图和左视图都是边长为4的正三角形,俯视图是一个半径为2的圆,那么这个几何体的全面积是 ( )A、8πcm2 B、10πcm2 C、12πcm2 D、16πcm24. 对某村一到六年级适龄儿童人数进行了统计,得到每个年级的儿童人数分别10,15,10,17,18,20.对于这组数据,下列说法错误的是( )A、平均数是15 B、众数是10 C、中位数是17 D、方差是5. 如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( )
3. 一个空间几何体的主视图和左视图都是边长为4的正三角形,俯视图是一个半径为2的圆,那么这个几何体的全面积是 ( )A、8πcm2 B、10πcm2 C、12πcm2 D、16πcm24. 对某村一到六年级适龄儿童人数进行了统计,得到每个年级的儿童人数分别10,15,10,17,18,20.对于这组数据,下列说法错误的是( )A、平均数是15 B、众数是10 C、中位数是17 D、方差是5. 如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( ) A、
A、 B、
B、 C、
C、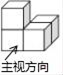 D、
D、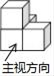 6. 某种颗粒每粒的质量为0.000000037克,500粒此种颗粒的质量用科学记数法可以表示为克,则的值是( )A、-5 B、-6 C、-7 D、-87. 如图,菱形ABCD的边AD⊥EF,垂足为点E,点H是菱形ABCD的对称中心.若FC= ,EF= DE,则菱形ABCD的边长为( )
6. 某种颗粒每粒的质量为0.000000037克,500粒此种颗粒的质量用科学记数法可以表示为克,则的值是( )A、-5 B、-6 C、-7 D、-87. 如图,菱形ABCD的边AD⊥EF,垂足为点E,点H是菱形ABCD的对称中心.若FC= ,EF= DE,则菱形ABCD的边长为( ) A、 B、3 C、4 D、58. 如图所示,在Rt△ABC中,AB=8,AC=6,∠CAB=90°,AD⊥BC,那么AD的长为( )
A、 B、3 C、4 D、58. 如图所示,在Rt△ABC中,AB=8,AC=6,∠CAB=90°,AD⊥BC,那么AD的长为( ) A、1 B、2 C、3 D、4.89. 已知二次函数y=x2-x+ , 当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2 , 则y1、y2满足( )
A、1 B、2 C、3 D、4.89. 已知二次函数y=x2-x+ , 当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2 , 则y1、y2满足( )
A、y1>0,y2>0 B、y1<0,y2>0 C、y1<0,y2<0 D、y1>0,y2<010. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )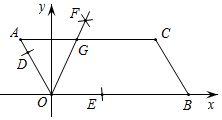 A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)
A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)二、填空题(每空4分,共24分)
-
11. 若Z= , 分解因式:x3y2﹣ax= .12. 我国“辽宁号”航空母舰的满载排水量为67500吨,将数据67500精确到千位的近似值为 . (结果用科学记数法表示)13. 在一个不透明的盒子中,装有除颜色外完全相同的乒乓球共16个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为 ,则该盒子中装有黄色兵乓球的个数是 .
14. 如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是 的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=. 15. 如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为.
15. 如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为. 16. 如图,已知顶点为 的抛物线 经过点 ,下列结论:① ;② ;③若点 在抛物线上,则 ;④关于 的一元二次方程 的两根为 和 ,其中正确的是.
16. 如图,已知顶点为 的抛物线 经过点 ,下列结论:① ;② ;③若点 在抛物线上,则 ;④关于 的一元二次方程 的两根为 和 ,其中正确的是.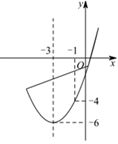
三、解答题(共7题,共66分)
-
17. 先化简,再求值:( )÷ ,其中x=2sin45°.18. 某校为了解初中学生每天在校体育活动的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
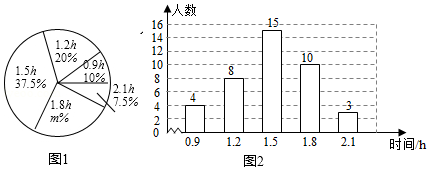 (1)、本次接受调查的初中学生人数为 , 图①中m的值为;(2)、求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;(3)、根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.19. 拉杆旅行箱为人们的出行带来了极大的方便,右图是一种拉杆旅行箱的侧面示意图,箱体ABCD可视为矩形,其中AB为50cm,BC为30cm,点A到地面的距离AE为4cm,旅行箱与水平面AF成60°角,求箱体的最高点C到地面的距离.
(1)、本次接受调查的初中学生人数为 , 图①中m的值为;(2)、求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;(3)、根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.19. 拉杆旅行箱为人们的出行带来了极大的方便,右图是一种拉杆旅行箱的侧面示意图,箱体ABCD可视为矩形,其中AB为50cm,BC为30cm,点A到地面的距离AE为4cm,旅行箱与水平面AF成60°角,求箱体的最高点C到地面的距离. 20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为 .
20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为 .
( 1 )请在如图所示的网格内作出x轴、y轴;
( 2 )请作出∆ABC关于y轴对称的∆ , 并写出点的坐标;
( 3 )求出∆的面积.
21.如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.

(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.22.在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
 23.
23.已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.
