2023年浙江省杭州市初中毕业生学业水平测试数学模拟试题(一)

试卷更新日期：2023-04-30 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列命题是真命题的是（）

A、内错角相等 B、三角形的内角和等于180° C、相等的角是对顶角 D、如果一个数是无限小数，那么这个数是无理数

查看试题解析
2. 下列平面图形中，既是中心对称图形，又是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 一个几何体的三视图如图所示，则这个几何体的侧面积是（）

A、 $27 π {cm}^{2}$ B、 $48 π {cm}^{2}$ C、 $96 π {cm}^{2}$ D、 $36 π {cm}^{2}$

查看试题解析
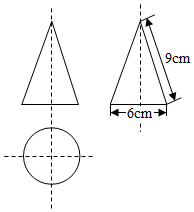4. 某棵果树前x年的总产量y与x之间的关系如图所示，从目前记录的结果看，前x年的年平均产量最高，则x的值为（）

A、3 B、5 C、7 D、9

查看试题解析
5. 如图是由大小相同的正方体搭成的几何体，将小正方体①去掉后，下列说法正确的是（）

A、主视图不变 B、俯视图不变 C、左视图不变 D、三种视图都不变

查看试题解析
6. 2020年2月11日在日内瓦，世卫组织总干事谭德塞在记者会上宣布，将新型冠状病毒（2019-nCov）引发的疾病正式命名为：2019冠状病毒病，（COVID-19，即Corona Virus Disease 2019），大小约为 $40 - 60 nm$ $(1 n m = 0.000000001 m)$ ，有包膜，基因特征与SARS-Cov有区别。用科学记数法表示 $58 nm$ 等于（）米.

A、 $58 \times 10^{- 8}$ B、 $58 \times 10^{- 9}$ C、 $5.8 \times 10^{- 8}$ D、 $5.8 \times 10^{- 9}$

查看试题解析
7. 如图，AB为⊙O的直径，AB=10cm，弦CD⊥AB，垂足为E，且AE：EB=2：3，则AC=（）

A、3cm B、4cm C、 cm D、 cm

查看试题解析
8. 如图，在Rt△ABC 中∠ACB = 90° ， AC = 3 ，BC = 4 ，点 D在 AB上， AD = AC ， AF⊥CD 交CD 于点 E ，交CB 于点 F ，则CF 的长是（）

A、2.5 B、2 C、1.8 D、1.5

查看试题解析
9. 若二次函数y＝x²+ $\frac{1}{2}$ 与y＝－x²+k的图象的顶点重合，则下列结论不正确的是（）

A、这两个函数图象有相同的对称轴 B、这两个函数图象的开口方向相反 C、方程－x²+k＝0没有实数根 D、二次函数y＝－x²＋k的最大值为 $\frac{1}{2}$

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中，点M为 $C D$ 的中点， $A M$ 与 $B D$ 相交于点N，若已知 $S_{△ D M N} = 3$ ，那么 $S_{△ A D N}$ 等于（）

A、6 B、9 C、12 D、3

查看试题解析

二、填空题（每空4分，共24分）

11. 分解因式： $16 x^{4} - 1 =$ .

查看试题解析
12. 某人一天饮水1890毫升，将1890精确到1000后可以表示为.

查看试题解析
13. 一个质地均匀的小正方体，6个面分别标有数字1，2，3，4，5，6．若随机投掷一次小正方体，则朝上一面的数字是3的概率是．

查看试题解析
14. 如图，在直角坐标系中，⊙A的圆心A的坐标为（﹣1，0），半径为1，点P为直线y=﹣ $\frac{3}{4}$ x+3上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是．

查看试题解析
15. 如图，长方形ABOC中点A坐标为（4，5），点E是x轴上一动点，连接AE，把∠B沿AE折叠，当点B落在y轴上时点E的坐标为．

查看试题解析
16. 如图1是一种阳台户外伸缩晾衣架，侧面示意图如图2所示，其支架AB，CD，EF，GH，BE，DG，FK的长度都为40cm（支架的宽度忽略不计），四边形BQCP、DMEQ、FNGM是互相全等的菱形，当晾衣架的A端拉伸到距离墙壁最远时，∠B=∠D=∠F=80°，这时A端到墙壁的距离约为cm．
（sin40°≈0.643，cos40°≈0.766，tan40°≈0.839）

查看试题解析

三、解答题（共7题，共66分）

17. 化简下列各式：

(1)、（a﹣2b）²+（a﹣b）（a+4b）；

(2)、 $\frac{x^{2} - 9}{x + 2} \div (\frac{6 x + 13}{x + 2} + x - 2)$ .

查看试题解析
18. 某台风给香港造成了重大的损失，某中学开展爱心捐助活动，根据预备年级的捐款情况绘制如下统计图：

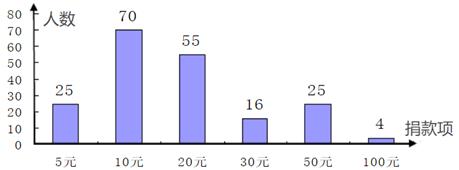
请根据统计图给出得信息回答下列问题：

(1)、本次活动中预备年级共有名同学捐款？

(2)、本次活动种捐款20元以上（不包括捐款20元的）人数占预备年级捐款总人数的几分之几？（写出过程）

查看试题解析
19.
放风筝是大家喜爱的一种运动．星期天的上午小明在大洲广场上放风筝．如图他在A处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D处．此时风筝线AD与水平线的夹角为30°．为了便于观察．小明迅速向前边移动边收线到达了离A处7米的B处，此时风筝线BD与水平线的夹角为45°．已知点A、B、C在冋一条直线上，∠ACD=90°．请你求出小明此吋所收回的风筝线的长度是多少米？（本题中风筝线均视为线段， $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732．最后结果精确到1米）

查看试题解析
20. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $A (- 2 ， 1)$ ， $B (1 ， n)$ 两点.

$($ Ⅰ $)$ 试确定上述反比例函数和一次函数的表达式；

$($ Ⅱ $)$ 连OB，在x轴上取点C，使 $B C = B O$ ，并求 $△ O B C$ 的面积；

$($ Ⅲ $)$ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.

查看试题解析
21. 如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B $\overset{⌢}{C E}$ 的中点，过点B的切线与AC的延长线交于点D.

①求证：BD⊥AD；

②若AC＝9，tan∠ABC＝ $\frac{3}{4}$ ，求⊙O的半径.

查看试题解析
22.
如图，一块平行四边形场地ABCD，测得∠ABC=60°，AB=2，AD=4，AE⊥BD于点E，CF⊥BD于点F，连接CE，AF．现计划在四边形AECF区域内种植花草．
（1）求证：四边形AECF是平行四边形；
（2）求四边形AECF的面积．

查看试题解析
23. 将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．

(1)、求证：AF+EF=DE；

(2)、若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；

(3)、若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．

查看试题解析