2023年浙江省绍兴市初中毕业生学业水平测试数学模拟试题(五)

试卷更新日期：2023-04-30 类型：中考模拟

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列各组数中，互为相反数的是（　　）

A、2和﹣2 B、﹣2和 $\frac{1}{2}$ C、﹣2和- $\frac{1}{2}$ D、 $\frac{1}{2}$ 和2

查看试题解析
2. 芜湖地处长江中下游，水资源丰富，素有“江南水乡”之美称．据测量，仅浅层地下水蕴藏量就达56000万m³ ，用科学记数法记作（　　）

A、5.6×10⁹m³ B、56×10⁸m³ C、5.6×10⁸m³ D、56000×10⁴m³

查看试题解析
3. 四个选项中四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体其中有三个几何体的某一种视图都是同一种几何图形，则另外一个几何体是（）

A、 B、 C、 D、

查看试题解析
4. 现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为 $x$ 、小明掷B立方体朝上的数字为 $y$ 来确定点P（ $x ， y$ ），那么他们各掷一次所确定的点P落在已知抛物线 $y = - x^{2} + 4 x$ 上的概率为（）

A、 $\frac{1}{18}$ B、 $\frac{1}{12}$ C、 $\frac{1}{9}$ D、 $\frac{1}{6}$

查看试题解析
5. 下列计算正确的是（）

A、 ${(a^{4} b)}^{3} = a^{7} b^{3}$ B、 $- 2 b (4 a - 1) = - 8 a b - 2 b$ C、 $a \times a^{3} + {(a^{2})}^{2} = 2 a^{4}$ D、 ${(a - 1)}^{2} = a^{2} - 1$

查看试题解析
6. 如图，小明从A处出发沿北偏东 $60 °$ 方向行走至B处，又沿北偏西 $20 °$ 方向行走至C处，则 $∠ A B C$ 的度数是（）

A、 $100 °$ B、 $90 °$ C、 $80 °$ D、 $70 °$

查看试题解析
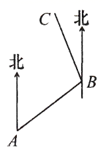7. 为了建设社会主义新农村，我市积极推进“行政村通畅工程”，对甲村和乙村之间的道路需要进行改造，施工队在工作了一段时间后，因暴雨被迫停工几天，不过施工队随后加快了施工进度，按时完成了两村之间道路的改造．下面能反映该工程改造道路里程 $y$ （公里）与时间 $x$ （天）的函数关系大致的图像是（）．

A、 B、 C、 D、

查看试题解析
8.
如图，矩形ABCD中，F是DC上一点，BF⊥AC，垂足为E， $\frac{A D}{A B} = \frac{1}{2}$ ， △CEF的面积为S₁ ， △AEB的面积为S₂ ，则 $\frac{S_{1}}{S_{2}}$ 的值等于（　　）

A、 $\frac{1}{16}$ B、 $\frac{1}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{25}$

查看试题解析
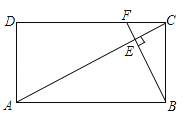9. 如图，抛物线y=ax²+bx+c，下列结论：①a＞0：②b²-4ac＞0：③4a+b=0；④不等式ax²+（b-1）x+c<0的解集为1<x<3，正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10. 在一条笔直的公路上有A、B两地，甲乙两人同时出发，甲骑自行车从A地到B地，乙骑自行车从B地到A地，到达A地后立即按原路返回B地.如图是甲、乙两人离B地的距离 $y (km)$ 与行驶时间 $x (h)$ 之间的函数图象，下列说法中①A、B两地相距30千米；②甲的速度为15千米/时；③点M的坐标为( $\frac{2}{3}$ ，20)；④当甲、乙两人相距10千米时，他们的行驶时间是 $\frac{4}{9}$ 小时或 $\frac{8}{9}$ 小时. 正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每空5分，共30分）

11. 已知a+b=2，a-b=-1，则a²-b²= ．

查看试题解析
12. 若 $\sqrt{a - 3} - 2 \sqrt{3 - a} = b + 6$ ，则a-b的算术平方根为．

查看试题解析
13. 程大位，明代珠算发明家，被称为珠算之父、卷尺之父．少年时，读书极为广博，对数学颇感兴趣，60岁时完成其杰作《直指算法统宗》(简称《算法统宗》)．《算法统宗》中有这样一道题，其大意为：有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：这一群人共有多少人？所分的银子共有多少两？若设共有x人，则可列方程为．

查看试题解析
14. 如图，AB是半圆的直径，点O为圆心，OA＝5，弦AC＝8，OD⊥AC，垂足为E，交⊙O于D，连接BE.设∠BEC＝α，则sinα的值为.

查看试题解析
15. 如图，在正方形ABCD中，E是CD边上一点，DE＝2，过B作AE的垂线，垂足为点F，BF＝3，将△ADE沿AE翻折，得到△AGE，AG与BF于点M，连接BG，则△BMG的周长为

查看试题解析
16. 在古埃及，人们把三边之比为3：4：5的三角形称为“埃及三角形”，古埃及人用一张正方形纸片，将一边中点和对边的两个端点连结，就能得到“埃及三角形”，如图所示，在正方形ABCD中，点E、F、G分别是AB、BC、CD的中点，则图中为“埃及三角形”的是（至少写出两个）.

查看试题解析

三、解答题（共8题，共80分）

17. 化简求值：

(1)、（28a³﹣28a²﹣7a）÷7a，其中a= $\frac{3}{4}$ ．

(2)、[（5x+2y）（3x+2y）+（x+2y）（x﹣2y）]÷4x，其中x=2，y=﹣3．

查看试题解析
18. 某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了如图①②两幅不完整的统计图，请根据图中的信息解答下列问题．

(1)、九年级(1)班接受调查的学生共有多少名？

(2)、补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数．

查看试题解析
19. 司机小王开车从A地出发去B地送信，其行驶路s与行驶时间t之间的关系如图所示，当汽车行驶若干小时到达C地时，汽车发生了故障，需停车检修，修理了几小时后，为了按时赶到B地，汽车加快了速度，结果正好按时赶到，根据题意结合图回答下列问题：

(1)、上述问题中反映的是哪两个变量之间的关系？指出自变量和因变量．

(2)、汽车从A地到C地用了几小时？平均每小时行驶多少千米？

(3)、汽车停车检修了多长时间？车修好后每小时走多少千米？

查看试题解析
20.
假日，小强在广场放风筝．如图，小强为了计算风筝离地面的高度，他测得风筝的仰角为60°，已知风筝线BC的长为10米，小强的身高AB为1.55米，请你帮小强画出测量示意图，并计算出风筝离地面的高度．（结果精确到1米，参考数据 $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73 ）

查看试题解析
21.
如图，在△ABC中，D为AB上一点，⊙O经过B、C、D三点，∠COD=90°，∠ACD=∠BCO+∠BDO．
（1）求证：直线AC是⊙O的切线；
（2）若∠BCO=15°，⊙O的半径为2，求BD的长．

查看试题解析
22. “扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量 $y$ （件）与销售单价 $x$ （元）之间存在一次函数关系，如图所示.

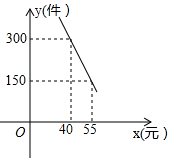(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.

查看试题解析
23. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ；

$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$

$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$

请你根据以上三个等式提供的信息解答下列问题

(1)、猜想： $\sqrt{1 + \frac{1}{7^{2}} + \frac{1}{8^{2}}} =$ =

(2)、归纳：根据你的观察，猜想，请写出一个用n(为正整数)表示的等式：

(3)、应用：计算 $\sqrt{\frac{82}{81} + \frac{1}{100}} =$

查看试题解析
24. 如图，在网格中，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点 $A$ 、 $B$ 、 $C$ 、 $D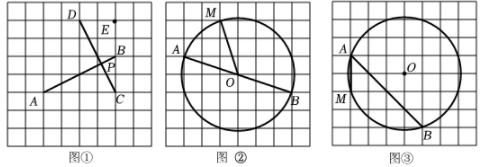$ 、 $M$ 均为格点.

(1)、【操作探究】在数学活动课上，佳佳同学在如图①的网格中，用无刻度的直尺画了两条互相垂直的线段 $A B$ 、 $C D$ ，相交于点 $P$ 并给出部分说理过程，请你补充完整：

解：在网格中取格点 $E$ ，构建两个直角三角形，分别是△ABC和△CDE.

在Rt△ABC中， $t a n ∠ B A C = \frac{1}{2}$

在Rt△CDE中，，

所以 $t a n ∠ B A C = t a n ∠ D C E$ .

所以∠ $B A C$ =∠ $D C E$ .

因为∠ $A C P +$ ∠ $D C E$ =∠ $A C B$ =90°，

所以∠ $A C P$ +∠ $B A C$ =90°，

所以∠ $A P C$ =90°，

即 $A B$ ⊥ $C D$ .

(2)、【拓展应用】如图②是以格点 $O$ 为圆心， $A B$ 为直径的圆，请你只用无刻度的直尺，在 $\overset{⌢}{B M}$ 上找出一点P，使 $\overset{⌢}{P M} = \overset{⌢}{A M}$ ，写出作法，并给出证明：

(3)、【拓展应用】如图③是以格点 $O$ 为圆心的圆，请你只用无刻度的直尺，在弦 $A B$ 上找出一点P.使 $A M^{2}$ = $A P$ · $A B$ ，写出作法，不用证明.

查看试题解析