2023年浙江省绍兴市初中毕业生学业水平测试数学模拟试题(四)
试卷更新日期:2023-04-30 类型:中考模拟
一、单选题(每题4分,共40分)
-
1. 在实数3π, , 0.2112111211112……(每两个2之多一个1), , 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 小明用如图所示的扇形纸片折叠成一个圆锥的侧面,已知圆锥的母线长为5cm,扇形的弧长是6 cm,那么这个圆锥的高是( )
3. 小明用如图所示的扇形纸片折叠成一个圆锥的侧面,已知圆锥的母线长为5cm,扇形的弧长是6 cm,那么这个圆锥的高是( ) A、4cm B、6cm C、8cm D、3cm4. 在一次体检中,甲、乙、丙、丁四位同学的平均身高为1.65米,而甲、乙、丙三位同学的平均身高为1.63米,下列说法一定正确的是( )A、四位同学身高的中位数一定是其中一位同学的身高 B、丁同学的身高一定高于其他三位同学的身高 C、丁同学的身高为1.71米 D、四位同学身高的众数一定是1.655. 某物体如图所示,它的俯视图为( )
A、4cm B、6cm C、8cm D、3cm4. 在一次体检中,甲、乙、丙、丁四位同学的平均身高为1.65米,而甲、乙、丙三位同学的平均身高为1.63米,下列说法一定正确的是( )A、四位同学身高的中位数一定是其中一位同学的身高 B、丁同学的身高一定高于其他三位同学的身高 C、丁同学的身高为1.71米 D、四位同学身高的众数一定是1.655. 某物体如图所示,它的俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.076微克,用科学记数法表示是( )A、0.76×10﹣2微克 B、7.6×10﹣2微克 C、76×102微克 D、7.6×102微克7. 如图,在5×4的正方形网格中,每个小正方形的边长都是l,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
6. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.076微克,用科学记数法表示是( )A、0.76×10﹣2微克 B、7.6×10﹣2微克 C、76×102微克 D、7.6×102微克7. 如图,在5×4的正方形网格中,每个小正方形的边长都是l,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )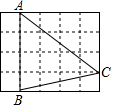 A、 B、 C、 D、8. 如图,在 中,分别以点A和B为圆心,大于 和长为半径画弧,两弧相交于点M,N,作直线 ,交 于点D,连接 ,若 的周长为 , ,则 的周长是( )
A、 B、 C、 D、8. 如图,在 中,分别以点A和B为圆心,大于 和长为半径画弧,两弧相交于点M,N,作直线 ,交 于点D,连接 ,若 的周长为 , ,则 的周长是( ) A、 B、 C、 D、9. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x= ,且经过点(2,0),下列说法:
A、 B、 C、 D、9. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x= ,且经过点(2,0),下列说法:①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(﹣2,y1),(﹣3,y2)是抛物线上的两点,则y1<y2 ,
其中说法正确的是( )
 A、①②④ B、③④ C、①③④ D、①②10. 如图,在中, , , , 且 , 若 , 点是线段上的动点,则的最小值是( )
A、①②④ B、③④ C、①③④ D、①②10. 如图,在中, , , , 且 , 若 , 点是线段上的动点,则的最小值是( )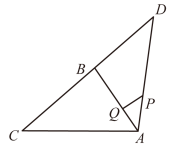 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空5分,共30分)
-
11. 因式分解:a4-1=。12. 圆周率 ,用四舍五入法把 精确到千分位,得到的近似值是.13. 如图,有两个转盘A、B,在每个转盘各自的两个扇形区域中分别标有数字 、 ,分别转动转盘A、B,当转盘停止转动时,若事件“指针都落在标有数字 的扇形区域内”的概率是 ,则转盘B中标有数字 的扇形的圆心角的度数是°.

 14. 如图,要测量小河两岸相对的两点P、A的距离,可以在小河边取PA的垂线PQ上的一点G,测得PG= 米,∠PGA=30°,则小河宽PA为米.
14. 如图,要测量小河两岸相对的两点P、A的距离,可以在小河边取PA的垂线PQ上的一点G,测得PG= 米,∠PGA=30°,则小河宽PA为米. 15. 如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.
15. 如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.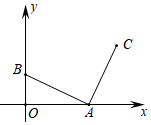 16. 如图, 于点A, 于点B,点P为线段AB上任意一点,若 , , ,则 的最小值是.
16. 如图, 于点A, 于点B,点P为线段AB上任意一点,若 , , ,则 的最小值是.
三、解答题(共8题,共80分)
-
17. 化简:(1)、(x-2y)(x+2y)-(x-2y) ;(2)、 .18. 已知a、b、c的大致位置如图所示:化简|a+c|+|b﹣c|﹣|a﹣b|.
 19. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
19. 如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼AB的高度进行测量.先测得居民楼AB与CD之间的距离AC为35m,后站在M点处测得居民楼CD的顶端D的仰角为45°.居民楼AB的顶端B的仰角为55°.已知居民楼CD的高度为16.6m,小莹的观测点N距地面1.6m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)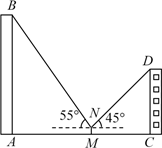 20. 某水果批发市场香蕉的价格如下表
20. 某水果批发市场香蕉的价格如下表购买香蕉数(千克)
不超过20千克
20千克以上但不超过40千克
40千克以上
每千克的价格
6元
5元
4元
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?
21. 如图,在△ABC中,点D , E分别是边AB , AC的中点,AF⊥BC , 垂足为点F , ∠ADE=30°,DF=3, ,求FC的长度. 22. 如图,一块平行四边形场地ABCD,测得∠ABC=60°,AB=2,AD=4,AE⊥BD于点E,CF⊥BD于点F,连接CE,AF.现计划在四边形AECF区域内种植花草.
22. 如图,一块平行四边形场地ABCD,测得∠ABC=60°,AB=2,AD=4,AE⊥BD于点E,CF⊥BD于点F,连接CE,AF.现计划在四边形AECF区域内种植花草.(1)求证:四边形AECF是平行四边形;
(2)求四边形AECF的面积.
 23. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
23. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .(Ⅰ)求抛物线的解析式和直线 的解析式;
(Ⅱ)当点 在线段 上运动时,求线段 的最大值;
(Ⅲ)当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.
 24. 已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.
24. 已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.
提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.