2023年浙江省绍兴市初中毕业生学业水平测试数学模拟试题(三)
试卷更新日期:2023-04-30 类型:中考模拟
一、单选题(每题4分,共40分)
-
1. 在下列实数中,无理数是( )A、 B、 C、 D、2. 剪纸是中国民间艺术的瑰宝,下列剪纸作品中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,从一块半径是 2 的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )
3. 如图,从一块半径是 2 的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( ) A、 B、 C、 D、4. 抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了如下统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
A、 B、 C、 D、4. 抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了如下统计图.根据如图提供的信息,红包金额的众数和中位数分别是( ) A、30,30 B、30,20 C、40,40 D、30,405. 如下图所示的几何体,它的俯视图是( )
A、30,30 B、30,20 C、40,40 D、30,405. 如下图所示的几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 国产手机芯片麒麟是全球首个纳米制程芯片,已知纳米米,将纳米用科学记数法表示为( )A、米 B、米 C、米 D、米7. 如图,的顶点O与坐标原点重合,顶点A,B分别在第二、三象限,且轴,若 , , 则点A的坐标为( )
6. 国产手机芯片麒麟是全球首个纳米制程芯片,已知纳米米,将纳米用科学记数法表示为( )A、米 B、米 C、米 D、米7. 如图,的顶点O与坐标原点重合,顶点A,B分别在第二、三象限,且轴,若 , , 则点A的坐标为( ) A、 B、 C、 D、8. 下面是教师出示的作图题.
A、 B、 C、 D、8. 下面是教师出示的作图题.已知:线段a,h,小明用如图所示的方法作 , 使 , 上的高 .

作法:①作射线 , 以点A为圆心、※为半径画弧,交射线于点B;②分别以点A,B为圆心、△为半径画弧,两弧交于点D,E;③作直线 , 交于点P;④以点P为圆心、为半径在上方画弧,交直线于点C,连接 , .
对于横线上符号代表的内容,下列说法错误的是()
A、※代表“线段a的长” B、△代表“任意长” C、△代表“大于的长” D、代表“线段h的长”9. 如图,二次函数的图象与x轴相交于 , B两点,对称轴是直线 , 下列说法正确的是( )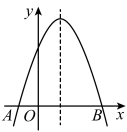 A、 B、当时,y的值随x值的增大而增大 C、点B的坐标为 D、10. 如图,在中, , 于点 . 点是上两点,且 , , 若 , . 则的值为( )
A、 B、当时,y的值随x值的增大而增大 C、点B的坐标为 D、10. 如图,在中, , 于点 . 点是上两点,且 , , 若 , . 则的值为( )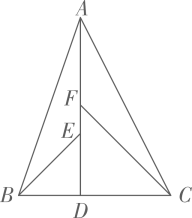 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空5分,共30分)
-
11. 已知长方形的面积是 ,一边长是 ,则长方形的周长是.12. 某公司组织内部抽奖活动,共准备了张奖券,设一等奖个,二等奖个,三等奖个.若每张奖券获奖的可能性相同,则随机抽一张奖券中一等奖的概率为 .13. 科技小组为了验证某电路的电压、电流电阻三者之间的关系: , 测得数据如表格:那么,当电阻时,电流A.
2
4
6
9
18
9
6
4
14. 用计算器计算:.(结果精确到0.01)15. 如图,甲楼AB高16米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1: , 已知两楼相距BD为12米,那么甲楼的影子落在乙楼上的高DE=米(结果保留根号). 16. 如图,正方形ABCD的边长为2,G是对角线BD上一动点,GE⊥CD于点E,GF⊥BC于点F,连结EF.给出四种情况:
16. 如图,正方形ABCD的边长为2,G是对角线BD上一动点,GE⊥CD于点E,GF⊥BC于点F,连结EF.给出四种情况:
①若G为BD上任意一点,则AG=EF;
②若BG=AB,则∠DAG=22.5°;
③若G为BD的中点,则四边形CEGF是正方形;
④若DG:BG=1:3,则S△ADG=
则其中正确的是.
三、解答题(共8题,共80分)
-
17.(1)、化简:(2)、解不等式:.18. 如图,数轴上有a,b,c三点,化简:.
 19. 如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B的中点,过点B的切线与AC的延长线交于点D.
19. 如图,⊙O是△ABC的外接圆,AE是⊙O的直径,点B的中点,过点B的切线与AC的延长线交于点D.
①求证:BD⊥AD;
②若AC=9,tan∠ABC= , 求⊙O的半径.
20. 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.“冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物.某冬奥官方特许商品零售店购进了一批同一型号的“冰墩墩”和“雪容融”玩具,连续两个月的销售情况如下表:
月份
销售量/件
销售额/元
冰墩墩
雪容融
第1个月
120
40
17160
第2个月
150
60
22200
求此款“冰墩墩”和“雪容融”玩具的零售价格.
解题方案:设此款“冰墩墩”玩具的零售价格为元,“雪容融”玩具的零售价格为元,
(Ⅰ)根据题意,列出方程组
(Ⅱ)解这个方程组,得
答:此款“冰墩墩”玩具的零售价格为元,“雪容融”玩具的零售价格为元.
21. 如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?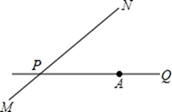 22. 在①;②;③这三个条件中任选一个补充在下面横线上,并完成证明过程.
22. 在①;②;③这三个条件中任选一个补充在下面横线上,并完成证明过程.已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上,(填写序号).
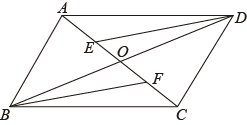
求证:四边形DEBF是平行四边形.
23. 如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ,x1•x2= ) (1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(3)、在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.24. 旋转的图形带来结论的奥秘.已知 , 将绕点逆时针旋转得到.初步探索
素材1:

如图①,连接对应点 , , 则.
素材2:

如图②,以为圆心,边上的高为半径作 , 则与相切.
问题解决
(1)(ⅰ)请证明素材1所发现的结论.
(ⅱ)如图2,过点作 , 垂足为.证明途径可以用下面的框图表示,请填写其中的空格.

深入研究
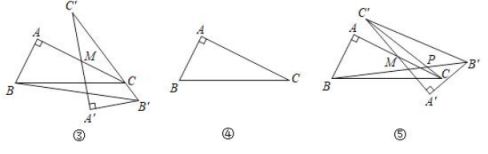
(2)在满足 , , 是的中点,绕点逆时针旋转得.
(ⅰ)如图③,当边恰好经过点时,连接 , 则的长为▲ .
(ⅱ)若一时边所在直线恰好经过点 , 于图④中利用无刻度的直尺和圆规作出直线.(只保留作图痕迹)
(3)在(2)的条件下,如图⑤,在旋转过程中,直线 , 交于点 , 求的最大值为▲ .