2023年浙江省绍兴市初中毕业生学业水平测试数学模拟试题 (二)
试卷更新日期:2023-04-30 类型:中考模拟
一、单选题(每题4分,共40分)
-
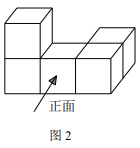
1. 的绝对值是( )A、-2023 B、2023 C、 D、2. 2023年春节期间,我省文化和旅游经济呈现“总体回暖,强势复苏”的可喜局面,其中体现巴蜀文化风韵的川渝春晚网络话题反响热烈,累计阅读量超过亿人次.将数据亿用科学记数法表示为( )A、 B、 C、 D、3. 如图2,是由相同大小的五个小正方体组成的立体模型,它的俯视图是( )
 A、
A、 B、
B、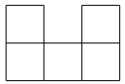 C、
C、 D、
D、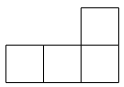 4. 下列命题中,假命题是( )A、平行四边形的对角线相等 B、正方形的对角线互相垂直平分 C、对角线互相垂直的平行四边形是菱形 D、有一个角为的平行四边形是矩形5. 为迎接体育中考,九年级班八名同学课间练习垫排球,记录成绩个数如下:40,38,42,35,45,40,42,42,则这组数据的众数与中位数分别是( )A、40,41 B、42,41 C、41,42 D、41,406. 若反比例函数y=(k<0)的图象经过A(-2,a),B(-3,b),C(2,c)三点,则a,b,c的大小关系正确的是( )A、a>b>c B、c>b>a C、a>c>b D、c>a>b7. 如图,在Rt△ABC中,∠C=90°,点D在斜边AB上,以BD为直径的⊙O经过边AC上的点E,连接BE,且BE平分∠ABC.若⊙O的半径为3,AD=2,则线段BC的长为( )
4. 下列命题中,假命题是( )A、平行四边形的对角线相等 B、正方形的对角线互相垂直平分 C、对角线互相垂直的平行四边形是菱形 D、有一个角为的平行四边形是矩形5. 为迎接体育中考,九年级班八名同学课间练习垫排球,记录成绩个数如下:40,38,42,35,45,40,42,42,则这组数据的众数与中位数分别是( )A、40,41 B、42,41 C、41,42 D、41,406. 若反比例函数y=(k<0)的图象经过A(-2,a),B(-3,b),C(2,c)三点,则a,b,c的大小关系正确的是( )A、a>b>c B、c>b>a C、a>c>b D、c>a>b7. 如图,在Rt△ABC中,∠C=90°,点D在斜边AB上,以BD为直径的⊙O经过边AC上的点E,连接BE,且BE平分∠ABC.若⊙O的半径为3,AD=2,则线段BC的长为( ) A、 B、8 C、 D、8. 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A(0,a)、B(-3,2)、C(c,m)、D(d,m),则点E的坐标是( )
A、 B、8 C、 D、8. 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A(0,a)、B(-3,2)、C(c,m)、D(d,m),则点E的坐标是( )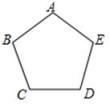 A、(2,-3) B、(2,3) C、(3,-2) D、(3,2)9. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作平行四边形AEDF,设BE=x,平行四边形AEDF的面积为y,则y与x之间的关系描述正确的是( )
A、(2,-3) B、(2,3) C、(3,-2) D、(3,2)9. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作平行四边形AEDF,设BE=x,平行四边形AEDF的面积为y,则y与x之间的关系描述正确的是( ) A、y与x之间是函数关系,且当x增大时,y先增大再减小 B、y与x之间是函数关系,且当x增大时,y先减小再增大 C、y与x之间是函数关系,且当x增大时,y一直保持不变 D、y与x之间不是函数关系10. 在平面直角坐标系xOy中,点A在直线上l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E,给出如下定义:若线段OE,⊙A和直线1上分别存在点B,点C和点D,使得四边形ABCD是矩形(点A,B.C,D顺时针排列),则称矩形ABCD为直线的“理想矩形.例如,图中的矩形ABCD为直线1的“理想矩形”,若点A(3,4),则直线y=kx+1(k≠0)的“理想矩形”的面积为( )
A、y与x之间是函数关系,且当x增大时,y先增大再减小 B、y与x之间是函数关系,且当x增大时,y先减小再增大 C、y与x之间是函数关系,且当x增大时,y一直保持不变 D、y与x之间不是函数关系10. 在平面直角坐标系xOy中,点A在直线上l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E,给出如下定义:若线段OE,⊙A和直线1上分别存在点B,点C和点D,使得四边形ABCD是矩形(点A,B.C,D顺时针排列),则称矩形ABCD为直线的“理想矩形.例如,图中的矩形ABCD为直线1的“理想矩形”,若点A(3,4),则直线y=kx+1(k≠0)的“理想矩形”的面积为( )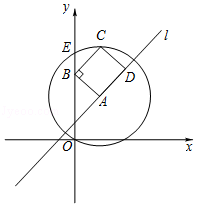 A、12 B、3 C、4 D、3
A、12 B、3 C、4 D、3二、填空题(每空5分,共30分)
-
11. 分解因式: .12. 已知一个多边形的每个内角都相等,其内角和为2340°,则这个多边形每个外角的度数是°.13. 关于 的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为.
 14. 如图,AB是⊙O的直径,弦CD⊥AB于点E,AB=4,CD=2 , 则BE的长度是
14. 如图,AB是⊙O的直径,弦CD⊥AB于点E,AB=4,CD=2 , 则BE的长度是 15. 如图,在边长相同的小正方形组成的网格中,点、、、都在这些小正方形的顶点上,线段、 , 相交于点 , 则的值是 .
15. 如图,在边长相同的小正方形组成的网格中,点、、、都在这些小正方形的顶点上,线段、 , 相交于点 , 则的值是 . 16. 如图,一块拼图卡片的长度为 厘米,两块相同的拼图卡片拼接在一起的长度为9厘米,则将 块相同的拼图卡片拼接在一起的长度为厘米.(用含 的式子表示)
16. 如图,一块拼图卡片的长度为 厘米,两块相同的拼图卡片拼接在一起的长度为9厘米,则将 块相同的拼图卡片拼接在一起的长度为厘米.(用含 的式子表示)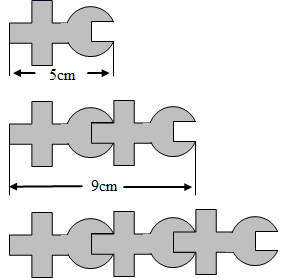
三、解答题(共8题,共80分)
-
17. 计算:18. 某报社为了解读者对本社一种报纸四个版面的喜爱情况,对读者作了一次问卷调查,要求读者选出最喜欢的一个版面,将所得数据整理绘制成了如下的条形统计图:
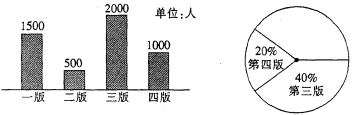 (1)、请写出从条形统计图中获得的一条信息;(2)、请根据条形统计图中的数据补全扇形统计图(要求:第二版与批三版相邻),并说明这两幅统计图各有什么特点?(3)、请你根据上述数据,对该报社提出一条合理的建议.19. 某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.(1)、设该学校所买的电脑台数是x台,选择甲商场时,所需费用为元,选择乙商场时,所需费用为元,请分别写出 , 与x之间的关系式;(2)、该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?20. 成都新世纪环球中心被誉为亚洲第一大单体建筑,可容纳20个悉尼歌剧院,3个五角大楼.某校开展综合实践活动,测量环球中心主体顶端A离地面的高度的长,如图,在观测点C处测得建筑物顶端A的仰角为 , 在观测点C测得建筑物底部B的俯角为 , 观测点C与建筑物的水平距离为120米,且垂直于(点A,B,C,D在同一平面内).求环球中心主体顶端A离地面的高度的长.(结果精确到1米;参考数据: , , , )
(1)、请写出从条形统计图中获得的一条信息;(2)、请根据条形统计图中的数据补全扇形统计图(要求:第二版与批三版相邻),并说明这两幅统计图各有什么特点?(3)、请你根据上述数据,对该报社提出一条合理的建议.19. 某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.(1)、设该学校所买的电脑台数是x台,选择甲商场时,所需费用为元,选择乙商场时,所需费用为元,请分别写出 , 与x之间的关系式;(2)、该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?20. 成都新世纪环球中心被誉为亚洲第一大单体建筑,可容纳20个悉尼歌剧院,3个五角大楼.某校开展综合实践活动,测量环球中心主体顶端A离地面的高度的长,如图,在观测点C处测得建筑物顶端A的仰角为 , 在观测点C测得建筑物底部B的俯角为 , 观测点C与建筑物的水平距离为120米,且垂直于(点A,B,C,D在同一平面内).求环球中心主体顶端A离地面的高度的长.(结果精确到1米;参考数据: , , , ) 21. 如图①, 是 的弦, ,垂足为P , 交 于点E , 且 , .
21. 如图①, 是 的弦, ,垂足为P , 交 于点E , 且 , .
(Ⅰ)求 的半径;
(Ⅱ)如图②,过点E作 的切线 ,连接 并延长与该切线交于点D , 延长 交 于C , 求 的长.
22. 课堂上,同学们在讨论解答数学课本50页综合运用的第9题“如图,在梯形ABCD中,AB∥CD,已知∠A=∠B,求证AD=BC.”时,提出了两种解答思路:思路1:过一个顶点作另一条腰的平行线,将梯形转化为等腰三角形和平行四边形;
思路2:过同一底上的两个顶点作另一底的垂线段,将梯形转化为直角三角形和矩形;请结合以上思路,选用一种方法证明上题.
 23. 已知抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 .点 是点 关于抛物线对称轴的对称点.过 , 两点的直线与 轴交于点 .
23. 已知抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 .点 是点 关于抛物线对称轴的对称点.过 , 两点的直线与 轴交于点 .(Ⅰ)求 , 两点的坐标;
(Ⅱ)若点 是抛物线上的点,点 的横坐标为 ,过点 作 轴,垂足为 .线段 与直线 交于点 ,当 时,求点 的坐标;
(Ⅲ)若点 是 轴上的点,且满足 ,求点 的坐标.
24. 在平面直角坐标系中,O为原点, 是等腰直角三角形, ,顶点 ,点B在第一象限,矩形 的顶点 ,点C在y轴的正半轴上,点D在第二象限,射线 经过点B.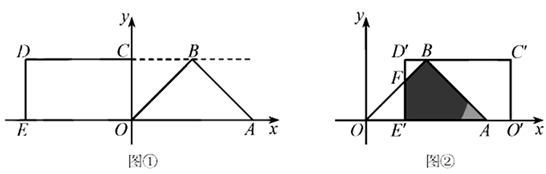
(Ⅰ)如图①,求点B的坐标;
(Ⅱ)将矩形 沿x轴向右平移,得到矩形 ,点O,C,D,E的对应点分别为 , , , ,设 ,矩形 与 重叠部分的面积为S.
①如图②,当点 在x轴正半轴上,且矩形 与 重叠部分为四边形时, 与 相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 时,求S的取值范围(直接写出结果即可).