2023年山西省中考模拟题人教版

试卷更新日期：2023-04-28 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 剪纸是中国民间艺术的瑰宝，下列剪纸作品中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列四个实数中，相反数最小的数是（）

A、 $- 1$ B、 $0$ C、 $\sqrt{5}$ D、 $- \frac{1}{3}$

查看试题解析
3. 中华人民共和国第十四届人民代表大会第一次会议政府工作报告指出：2023年国内生产总值预期增长目标5%左右，城镇新增就业1200万人左右，将1200万用科学记数法表示为（）

A、 $12 \times 1 0^{6}$ B、 $1.2 \times 1 0^{7}$ C、 $1.2 \times 1 0^{8}$ D、 $0.12 \times 1 0^{8}$

查看试题解析
4. 下列计算正确的是（）

A、4a－2a＝2 B、 $a^{8} \div a^{4} = a^{2}$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 ${(b^{2})}^{3} = b^{5}$

查看试题解析
5. 如图所示，几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 我们在解一元二次方程 $(x + 1)^{2} - 9 = 0$ 时，先将等号左边利用平方差公式进行因式分解，得到 $(x + 1 + 3) (x + 1 - 3) = 0$ ，再把它转化为两个一元一次方程 $x + 1 + 3 = 0$ 或 $x + 1 - 3 = 0$ ，进而解得 $x_{1} = - 4$ ， $x_{2} = 2$ ，这种解方程的过程体现出来的数学思想是（　　）

A、抽象的思想 B、数形结合的思想 C、公理化的思想 D、转化的思想

查看试题解析
7. 已知关于x的一元二次方程 $k x^{2} - 4 \sqrt{2} x + 2 = 0$ 有两个不相等的实数根，则k的取值范围是（）

A、 $k < 4$ B、 $k < 4$ 且 $k \neq 0$ C、 $k \geq - 4$ 且 $k \neq 0$ D、 $k \leq - 4$ 且 $k \neq 0$

查看试题解析
8. 如图，点A、C为反比例函数 $y = \frac{k}{x} (x < 0)$ 图象上的点，过点A、C分别作 $A B ⊥ x$ 轴， $C D ⊥ x$ 轴，垂足分别为B、D，连接 $O A$ 、 $A C$ 、 $O C$ ，线段 $O C$ 交 $A B$ 于点E，点E恰好为 $O C$ 的中点，当 $Δ A E C$ 的面积为6时，k的值为（）

A、 $- 16$ B、8 C、 $- 8$ D、 $- 12$

查看试题解析
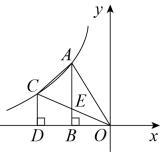9. 已知实数 $a \neq b$ ，且满足 $(a + 1)^{2} = 3 - 3 (a + 1)$ ， $(b + 1)^{2} = 3 - 3 (b + 1)$ ，则 $b \sqrt{\frac{b}{a}} + a \sqrt{\frac{a}{b}}$ 的值为（）

A、23 B、-23 C、-2 D、-13

查看试题解析
10. 如图，△ABC是一块锐角三角形材料，高线AH长8 cm，底边BC长10 cm，要把它加工成一个矩形零件，使矩形DEFG的一边EF在BC上，其余两个顶点D，G分别在AB，AC上，则四边形DEFG的最大面积为（）

A、40 cm² B、20 cm² C、25 cm² D、10 cm²

查看试题解析

二、填空题

11. 化简： $\frac{2}{a - 2} - \frac{8}{a^{2} - 4} =$ ．

查看试题解析
12. 分解因式：x²－4x+4＝．

查看试题解析
13. 如图，在 $5 \times 5$ 的正方形网格飞镖游戏板中，每块小正方形除颜色外都相同，小正方形的顶点称为格点.假设飞镖击中每一块小正方形是等可能的，任意投掷飞镖一次，飞镖击中阴影部分的概率是.

查看试题解析
14. $▱ A B C D$ 中， $∠ B A C = 60 °$ ， $A C$ 、 $B D$ 相交于点 $O$ ，且 $∠ B O C = 2 ∠ A C B$ ，若 $A B = 4$ ，则 $B D$ 的长为．

查看试题解析
15. $△ A B C$ 中， $∠ A C B = 90 °$ ，把 $△ A B C$ 绕点A逆时针旋转 $α$ 度 $(0 ° < α < 90 °)$ ，得到 $△ A D E$ ，点B，C的对应点分别为点D，E，连接EC并延长交BD于点P.若 $s i n ∠ B A C = \frac{3}{5}$ ，则 $\frac{B P}{C E}$ 的值为.

查看试题解析

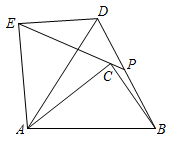
三、解答题

16. 计算：| $\sqrt{3}$ ﹣2|+3tan30°+（ $\frac{1}{2}$ ）^﹣1﹣（3﹣π）⁰﹣（ $\sqrt{2}$ ）² ．

查看试题解析
17. 先化简，再求值： $\frac{x - 1}{x^{2} - 1} \cdot \frac{x^{2} - 2 x + 1}{x - 4} - \frac{x}{x + 1}$ ，其中x=2 $\sqrt{2}$ ﹣1．

查看试题解析
18. 已知 $D A ， D C$ 分别与 $⊙ O$ 相切于点 $A ， C$ ，延长 $D C$ 交直径 $A E$ 的延长线于点 $P$ ．

(1)、如图①，若 $D C = P C$ ，求 $∠ P$ 的度数；

(2)、如图②，在 $⊙ O$ 上取一点 $B$ ，连接 $A B ， B C ， B E$ ，当四边形 $A B C D$ 是平行四边形时，求 $∠ P$ 及 $∠ A E B$ 的大小．

查看试题解析
19. 某校准备在甲、乙两家公司为毕业班学生制作一批纪念册．甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费．
（1）请写出制作纪念册的册数x与甲公司的收费y₁（元）的函数关系式．
（2）请写出制作纪念册的册数x与甲公司的收费y₂（元）的函数关系式．
（3）如果学校派你去甲、乙两甲公司订做纪念册，你会选择哪家公司？

查看试题解析
20.
某中学开展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．
班级
平均数（分）
中位数
众数
九（1）
85

85
九（2）

80

（1）根据图示填写上表；
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差，并说明哪个班级的成绩较稳定．

查看试题解析
21. 在交城县城西北方向的卦山群峰中，位于中央的小山峰上屹立着一座白塔，它在卦山诸多名胜中最引人注目 $($ 如图 $1)$ ．某数学小组为测量白塔的高度，在 $A$ 处 $($ 如图 $2)$ 测得塔顶 $C$ 的仰角为 $45 °$ ，然后沿着斜坡 $A B$ 前进 $13$ 米到达 $B$ 处，在 $B$ 处测得到塔脚的距离 $B D = 15$ 米，已知 $t a n ∠ B A F = \frac{5}{12}$ ， $∠ E = 90 °$ ，求白塔的高度 $C D$ ．

查看试题解析

22. 先阅读下列材料，再解答问题．

尺规作图：

已知： $△ A B C$ ， D是边 $A B$ 上一点，如图1．

求作：四边形 $D B C F$ ，使得四边形 $D B C F$ 是平行四边形．

小明的做法如下：

⑴设计方案

先一个正确的草图，如图2，

再分析实现目标的具体方法．

⑵设计作图步骤，完成作图

作法：如图3，

①以点C为圆心、 $B D$ 为半径画弧；

②再以点D为圆心、 $B C$ 为半径画弧，两弧交于点F；

③连接 $D F$ 与 $C F$ ．

∴四边形 $D B C F$ 即为所求．

请在图3中完成尺规作图，保留作图痕迹

⑶推理论证

证明：∵ ，

∴四边形DBCF是平行四边形．（）（填推理依据）

查看试题解析

四、综合题

23. 如图1， $△ A B C$ 中， $∠ A C B = 90 ° ， A C = B C$ ，点D，E分别在边 $A C ， A B$ 上，且 $D E ∥ B C$ ．

(1)、则 $\frac{C D}{B E}$ 的值为；

(2)、将 $△ A D E$ 绕点A逆时针旋转到如图2的位置，旋转角为 $a (45 ° < a < 90 °)$ ，连接 $C D ， B E$ ，求 $\frac{C D}{B E}$ 的值；

(3)、将 $△ A D E$ 绕点A旋转，当 $∠ D E B = 90 ° ， A C = 5 ， A D = \sqrt{5}$ 时，请直接写出线段 $C D$ 的长．

查看试题解析
24. 如图，在平而直角坐标系中，抛物线 $y = a x^{2} + b x + 4$ 与x轴交于 $A (- 2 ， 0)$ ， $B (4 ， 0)$ 两点，与y轴交于点C．

(1)、试求抛物线的解析式；

(2)、直线 $y = k x + 1 (k > 0)$ 与y轴交于点D，与抛物线在第一象限交于点P，与直线 $B C$ 交于点M，记 $m = \frac{S_{△ C P M}}{S_{△ C D M}}$ ，试求m的最大值及此时点P的坐标；

(3)、在（2）的条件下，m取最大值时，是否存在x轴上的点Q及坐标平面内的点N，使得P，D，Q，N四点组成的四边形是矩形？若存在，请直接写出所有满足条件的Q点和N点的坐标：若不存在，请说明理由．

查看试题解析

班级	平均数（分）	中位数	众数
九（1）	85		85
九（2）		80

2023年山西省中考模拟题 人教版

一、单选题

二、填空题

三、解答题

四、综合题

2023年山西省中考模拟题人教版