江苏省扬州市宝应县东北片2022-2023学年九年级下学期3月月考数学试题
试卷更新日期:2023-04-28 类型:月考试卷
一、单选题
-
1. -2023的相反数等于( )A、 -2023 B、2023 C、±2023 D、2. 下列计算,正确的是( )A、 B、 C、 D、3. 下列展开图中,是正方体展开图的是( )A、
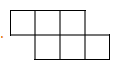 B、
B、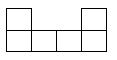 C、
C、 D、
D、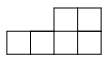 4. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果一间客房住7人,那么有7人无房可住;如果一间客房住9人,那么就空出一间客房,若设该店有客房x间,房客y人,则列出关于x、y的二元一次方程组正确的是( )A、 B、 C、 D、5. 如图,直线AB与CD相交于点O, , ,则 的度数是( )
4. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果一间客房住7人,那么有7人无房可住;如果一间客房住9人,那么就空出一间客房,若设该店有客房x间,房客y人,则列出关于x、y的二元一次方程组正确的是( )A、 B、 C、 D、5. 如图,直线AB与CD相交于点O, , ,则 的度数是( ) A、25° B、30° C、40° D、50°6. 在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )A、12π B、15π C、20π D、24π7. 二次函数 的图象如图所示,当 时 ,那么当 时,函数值( )
A、25° B、30° C、40° D、50°6. 在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )A、12π B、15π C、20π D、24π7. 二次函数 的图象如图所示,当 时 ,那么当 时,函数值( )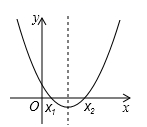 A、 B、 C、 D、8. 如图,在 ABCD中, , ,点E在AD上, ,则 的值是( )
A、 B、 C、 D、8. 如图,在 ABCD中, , ,点E在AD上, ,则 的值是( )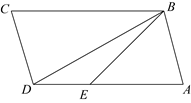 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
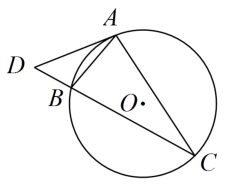
9. 已知一组数据:4,5,5,6,5,4,7,8,则这组数据的众数是.10. 若二次根式有意义,则实数x的取值范围是.11. 分解因式:.12. 地球上陆地的面积约为149 000 000平方千米,把数据149 000 000用科学记数法表示为13. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
 14. 如图,在中,是中线的中点.若的面积是1,则的面积是.
14. 如图,在中,是中线的中点.若的面积是1,则的面积是. 15. 若关于 的一元二次方程 的一个解是 ,则 的值是.16. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为.17. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.
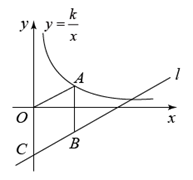
15. 若关于 的一元二次方程 的一个解是 ,则 的值是.16. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为.17. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.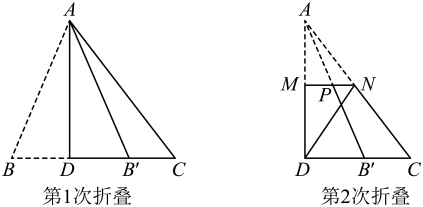 18. 如图,点A在双曲线 上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:
18. 如图,点A在双曲线 上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:① ②当 时, ③ ④
则所有正确结论的序号是 .
三、解答题
-
19.(1)、(2)、20. 解不等式组 , 并求出它的所有整数解的和.21. 每年的6月6日为“全国爱眼日”.某初中学校为了解本校学生视力健康状况,组织数学兴趣小组按下列步骤来开展统计活动.(1)、一,确定调查对象
有以下三种调查方案:
方案一:从七年级抽取140名学生,进行视力状况调查;
方案二:从七年级、八年级中各随机抽取140名生,进行视力状况调查;
方案三:从全校1600名学生中随机抽取600名学生,进行视力状况调查.
其中最具有代表性和广泛性的抽样调查方案是 ;
(2)、二,收集整理数据按照国家视力健康标准,学生视力状况分为A,B,C,D四个类别.数学兴趣小组随机抽取本校部分学生进行调查,绘制成如图一幅不完整的统计图.
抽取的学生视力状况统计表
类别
A
B
C
D
视力
视力
4.9
视力
视力
健康状况
视力正常
轻度视力不良
中度视力不良
重度视力不良
人数
160
m
n
56
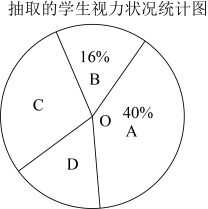
三,分析数据,解答问题
表中 , 调查视力数据的中位数所在类别为 类;
(3)、该校共有学生1600人,请估算该校学生中,中度视力不良和重度视力不良的总人数;22. “石头、剪子、布”是一个广为流传的游戏,规则是:甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种,其中“石头”赢“剪子”,“剪子”赢“布”,“布”赢“石头”,手势相同不分输赢.假设甲、乙两人每次都随意并且同时做出3种手势中的1种.(1)、甲每次做出“石头”手势的概率为;(2)、用画树状图或列表的方法,求乙不输的概率.23. 为了加强学生的体育锻炼,某班计划购买部分绳子和实心球.已知每条绳子的价格比每个实心球的价格少23元,且84元购买绳子的数量与360元购买实心球的数量相同,绳子和实心球的单价各是多少元?24. 如图,线段DE与AF分别为△ABC的中位线与中线.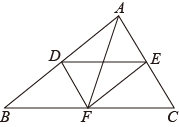 (1)、求证:AF与DE互相平分;(2)、当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.25. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC交AC于点E.
(1)、求证:AF与DE互相平分;(2)、当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.25. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC交AC于点E.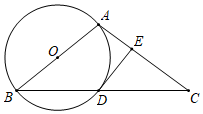 (1)、试判断直线DE与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为5,BC=16,求DE的长.26. 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如图,在中, , 顶角A的正对记作 , 这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:
(1)、试判断直线DE与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为5,BC=16,求DE的长.26. 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如图,在中, , 顶角A的正对记作 , 这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题: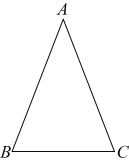 (1)、 的值为( ).A、 B、1 C、 D、2(2)、对于 , 的正对值的取值范围是.(3)、已知 , 其中α为锐角,试求的值.27. 某雨润肉店店主从市场行情了解到,在足够长的一段时间里,猪肉的进价均为20元/kg若该店月猪肉销量y(kg)与销售价格x(元)的关系如下表,且y是x的一次函数.
(1)、 的值为( ).A、 B、1 C、 D、2(2)、对于 , 的正对值的取值范围是.(3)、已知 , 其中α为锐角,试求的值.27. 某雨润肉店店主从市场行情了解到,在足够长的一段时间里,猪肉的进价均为20元/kg若该店月猪肉销量y(kg)与销售价格x(元)的关系如下表,且y是x的一次函数.800
2000
x(元)
30
24
(1)、求y与x的函数关系式;(2)、若在销售猪肉所获得利润的基础上,该店每月还需用其支付其它开支共4000元.试求该店销售猪肉所获得的月净利润p(元)与x(元)之间的函数关系式;(3)、在第(2)问的基础上,根据店主提供的数据,该肉店的猪肉月销售量至少为 , 则当销售价格为多少元时,p最大?并求出该最大值.28. 已知:正方形 , 等腰直角三角板的直角顶点落在正方形的顶点处,使三角板绕点旋转.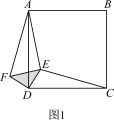
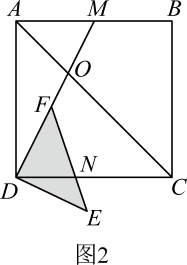 (1)、当三角板旋转到图1的位置时,猜想与的数量关系,并加以证明;(2)、在(1)的条件下,若 , 求的度数;(3)、若 , 点是边的中点,连结 , 与交于点 , 当三角板的边与边重合时(如图2),若 , 求的长.
(1)、当三角板旋转到图1的位置时,猜想与的数量关系,并加以证明;(2)、在(1)的条件下,若 , 求的度数;(3)、若 , 点是边的中点,连结 , 与交于点 , 当三角板的边与边重合时(如图2),若 , 求的长.