江苏省盐城市大丰区2022-2023学年九年级下学期3月月考数学试题
试卷更新日期:2023-04-28 类型:月考试卷
一、单选题
-
1. -2023的倒数是( )A、-2023 B、2023 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 下列四个汉字中,是轴对称图形的是( )A、我 B、爱 C、飞 D、中4. 近年来,我国新冠肺炎疫情防控工作一直在有序进行,经科学家研究,冠状病毒多数为球形或近似球形,其直径约为0.00000012米,其中数据0.00000012用科学记数法表示正确的是( )A、 B、 C、 D、5. 如果分式的值为0,那么x的值是( )A、 B、 C、或 D、或06. 如图,在平面直角坐标系中,菱形的边在轴上,点 , , 若反比例函数经过点 , 则的值是( )
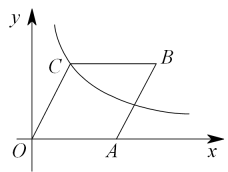 A、10 B、12 C、48 D、507. 已知二次函数y=x2-2x+2在m≤x≤m+1时有最小值m,则整数m的值是( )A、1 B、2 C、1或2 D、±1或28. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )
A、10 B、12 C、48 D、507. 已知二次函数y=x2-2x+2在m≤x≤m+1时有最小值m,则整数m的值是( )A、1 B、2 C、1或2 D、±1或28. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )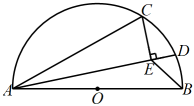 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
9. 单项式的次数为 .10. 分解因式:.11. =.12. 关于的方程有增根,则.13. 如图,的弦 , 过点O作于点C,交于点P,若 , 则的半径为.
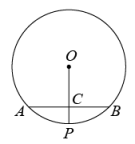 14. 若点 , 都在直线上,则的大小关系是 .15. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是
14. 若点 , 都在直线上,则的大小关系是 .15. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是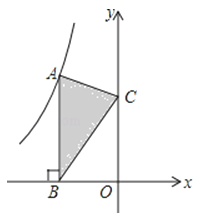 16. 如图,“爱心”图案是由函数的部分图像与其关于直线的对称图形组成.点A是直线上方“爱心”图案上的任意一点,点B是其对称点.若 , 则点A的坐标是.
16. 如图,“爱心”图案是由函数的部分图像与其关于直线的对称图形组成.点A是直线上方“爱心”图案上的任意一点,点B是其对称点.若 , 则点A的坐标是.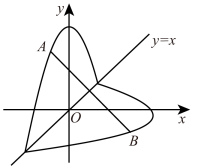
三、解答题
-
17. 计算:(1)、 ;(2)、 .18.(1)、解分式方程:;(2)、解不等式组:.19. 先化简,再求值:(1)、 ,其中;(2)、 ,其中.20. 如图,已知过点 的直线 与直线 : 相交于点 .
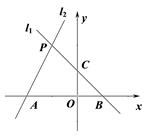 (1)、求直线 的解析式;(2)、求四边形 的面积.21. 如图,在平面直角坐标系中,将绕原点O顺时针旋转得到 .
(1)、求直线 的解析式;(2)、求四边形 的面积.21. 如图,在平面直角坐标系中,将绕原点O顺时针旋转得到 . (1)、画出 , 并写出点、的坐标;(2)、求出边在旋转变换过程中所扫过的图形的面积.22. 2023年3月12日,大丰区飞达路初级中学开展“为校园增添一点绿色”为主题的植树活动,组织七年级、八年级、九年级分别在12日、13日、14日进行植树活动,七年级学生在12日种植了25棵树苗,学生们在种植的过程中听老师讲解植树绿化的意义,热情高涨,每天的植树增长率相同,九年级学生在14日种植了49棵树苗.(1)、求平均每天植树的增长率?(2)、求此次活动三个年级种植树苗的总棵数?23. 在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成工程量x(米)是反比例函数关系,图象如图所示:
(1)、画出 , 并写出点、的坐标;(2)、求出边在旋转变换过程中所扫过的图形的面积.22. 2023年3月12日,大丰区飞达路初级中学开展“为校园增添一点绿色”为主题的植树活动,组织七年级、八年级、九年级分别在12日、13日、14日进行植树活动,七年级学生在12日种植了25棵树苗,学生们在种植的过程中听老师讲解植树绿化的意义,热情高涨,每天的植树增长率相同,九年级学生在14日种植了49棵树苗.(1)、求平均每天植树的增长率?(2)、求此次活动三个年级种植树苗的总棵数?23. 在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成工程量x(米)是反比例函数关系,图象如图所示: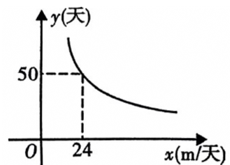 (1)、求y与x之间的函数关系式(2)、若该工程队有4台挖掘机,每台挖掘机每天能够开挖水渠30米,问该工程队需要用多少天才能完成此项任务?24. 疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机 等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为: .效果很好; .效果较好; .效果一般; .效果不理想)并根据调查结果绘制了如下两幅不完整的统计图:
(1)、求y与x之间的函数关系式(2)、若该工程队有4台挖掘机,每台挖掘机每天能够开挖水渠30米,问该工程队需要用多少天才能完成此项任务?24. 疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机 等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为: .效果很好; .效果较好; .效果一般; .效果不理想)并根据调查结果绘制了如下两幅不完整的统计图: (1)、此次调查中,共抽查了名学生;(2)、补全条形统计图,并求出扇形统计图中∠a的度数;(3)、某班 人学习小组,甲、乙 人认为效果很好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取 人,则“ 人认为效果很好, 人认为效果较好”的概率是多少?(要求画树状图或列表求概率)25. 在平面直角坐标系中,二次函数的图象经过两点.
(1)、此次调查中,共抽查了名学生;(2)、补全条形统计图,并求出扇形统计图中∠a的度数;(3)、某班 人学习小组,甲、乙 人认为效果很好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取 人,则“ 人认为效果很好, 人认为效果较好”的概率是多少?(要求画树状图或列表求概率)25. 在平面直角坐标系中,二次函数的图象经过两点.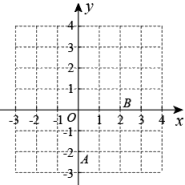 (1)、求这个二次函数的解析式;(2)、若一次函数的图象也经过A,B两点,结合图象,直接写出不等式的解集.26. 如图,在中,点是直径延长线上的一点,点是直径上方圆上的一点,连接 , 使得.
(1)、求这个二次函数的解析式;(2)、若一次函数的图象也经过A,B两点,结合图象,直接写出不等式的解集.26. 如图,在中,点是直径延长线上的一点,点是直径上方圆上的一点,连接 , 使得. (1)、求证:是的切线;(2)、若平分 , 且分别交 , 于点 , , 当时,求F的长;(3)、若 , , 求的长.27. 如图,直线y=-x+m与抛物线y=ax2+bx都经过点A(6,0),点B,过B作BH垂直x轴于H,OA=3OH.直线OC与抛物线AB段交于点C.
(1)、求证:是的切线;(2)、若平分 , 且分别交 , 于点 , , 当时,求F的长;(3)、若 , , 求的长.27. 如图,直线y=-x+m与抛物线y=ax2+bx都经过点A(6,0),点B,过B作BH垂直x轴于H,OA=3OH.直线OC与抛物线AB段交于点C. (1)、求抛物线的解析式;(2)、当点C的纵坐标是时,求直线OC与直线AB的交点D的坐标;(3)、在(2)的条件下将△OBH沿BA方向平移到△MPN,顶点P始终在线段AB上,求△MPN与△OAC公共部分面积的最大值.
(1)、求抛物线的解析式;(2)、当点C的纵坐标是时,求直线OC与直线AB的交点D的坐标;(3)、在(2)的条件下将△OBH沿BA方向平移到△MPN,顶点P始终在线段AB上,求△MPN与△OAC公共部分面积的最大值.