湖北省武汉市江夏区2022-2023学年八年级下学期期中考试数学试卷
试卷更新日期:2023-04-28 类型:期中考试
一、单选题
-
1. 若二次根式 有意义,则 x 的取值范围是( )A、 B、 C、 D、2. 在下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. △ABC中,∠A、∠B、∠C所对的边分别是a,b,c,则满足下列条件的△ABC不是直角三角形的是( )A、 B、 C、 D、5. 菱形的边长为5,它的一条对角线的长为6,则菱形的另一条对角线的长为( )A、8 B、6 C、5 D、46. 下列四个命题:①平行四边形的两组对角分别相等;②对角线互相垂直且平分的四边形是菱形;③矩形是轴对称图形;④对角线相等的菱形是正方形;其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个7. 如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
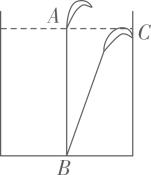 A、7.5尺 B、8尺 C、8.5尺 D、9尺8. 如图,已知矩形ABCD,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A、7.5尺 B、8尺 C、8.5尺 D、9尺8. 如图,已知矩形ABCD,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )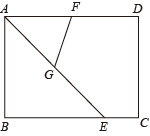 A、 B、 C、2 D、9. 如图,矩形ABCD的周长为1,连接矩形ABCD四条边中点得到四边形A1B1C1D1 , 再连接四边形A1B1C1D1四条边中点得到四边形A2B2C2D2 , 如此继续下去…,则四边形A10B10C10D10的周长为( )
A、 B、 C、2 D、9. 如图,矩形ABCD的周长为1,连接矩形ABCD四条边中点得到四边形A1B1C1D1 , 再连接四边形A1B1C1D1四条边中点得到四边形A2B2C2D2 , 如此继续下去…,则四边形A10B10C10D10的周长为( )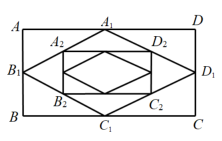 A、()5 B、()10 C、()5 D、()1010. 如图,矩形的顶点E、F分别在菱形的边和对角线上,连接 , 若 , , 当的长最小时,则的长为( )
A、()5 B、()10 C、()5 D、()1010. 如图,矩形的顶点E、F分别在菱形的边和对角线上,连接 , 若 , , 当的长最小时,则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算.12. 如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为 .
 13. 已知 , , , 则代数式的值为.14. 如图,将沿翻折得到 , 若 , , 则的度数为.
13. 已知 , , , 则代数式的值为.14. 如图,将沿翻折得到 , 若 , , 则的度数为.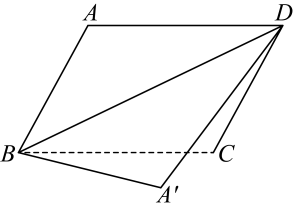 15. 中, , 是的边上的高,若 , , 则边的长度是.16. 如图,在四边形ABCD中, , , cm,cm,cm.点P从点A出发,以2cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.若运动t s时 , 则运动时间t的值是s.
15. 中, , 是的边上的高,若 , , 则边的长度是.16. 如图,在四边形ABCD中, , , cm,cm,cm.点P从点A出发,以2cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.若运动t s时 , 则运动时间t的值是s.
三、解答题
-
17. 计算(1)、(2)、18. 如图,在▱中, , 是AB,上的点,且 , 求证:四边形是平行四边形.
 19. 如图1,在中, , 于点C,点E是的中点,连接并延长,使 , 连接.
19. 如图1,在中, , 于点C,点E是的中点,连接并延长,使 , 连接.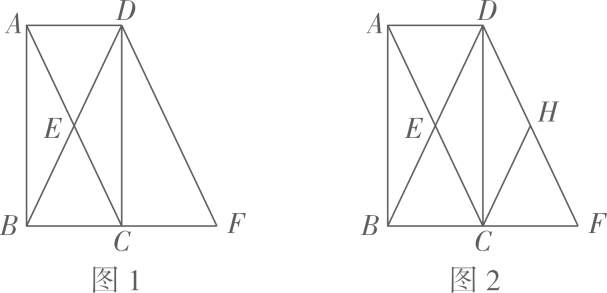 (1)、求证:四边形是矩形.(2)、如图2,点H为的中点,连结 , 若 , , 求四边形的面积.20. 如图是一个的网格图,每个小正方形的边长都为单位1,每一个小正方形的顶点叫做格点.图中已画出了线段和线段 , 其端点A,B,E,G均在小正方形的顶点上,点P是线段上一非格点,请按要求画出图形(过程用虚线,结果为实线)并计算.
(1)、求证:四边形是矩形.(2)、如图2,点H为的中点,连结 , 若 , , 求四边形的面积.20. 如图是一个的网格图,每个小正方形的边长都为单位1,每一个小正方形的顶点叫做格点.图中已画出了线段和线段 , 其端点A,B,E,G均在小正方形的顶点上,点P是线段上一非格点,请按要求画出图形(过程用虚线,结果为实线)并计算. (1)、画出以为边的正方形;(2)、画一个以为一条对角线的菱形(点F在的左侧),且;(3)、在(1)正方形的边上画一点Q,使得;(4)、在(1)中菱形的边上画一点M,使得经过点M的直线同时将菱形和正方形的面积二等分.21. 如图,在四边形中, , , , , .
(1)、画出以为边的正方形;(2)、画一个以为一条对角线的菱形(点F在的左侧),且;(3)、在(1)正方形的边上画一点Q,使得;(4)、在(1)中菱形的边上画一点M,使得经过点M的直线同时将菱形和正方形的面积二等分.21. 如图,在四边形中, , , , , . (1)、判断的形状,并说明理由;(2)、求的长.22. 如图,矩形内三个相邻的正方形的边长分别为m、n和1.
(1)、判断的形状,并说明理由;(2)、求的长.22. 如图,矩形内三个相邻的正方形的边长分别为m、n和1. (1)、求图中阴影部分的面积(用含m和n的式子表示);(2)、若 , , 求阴影部分的面积.23.(1)、【操作与探究】如图1,正方形中,点E、F分别是上一点.延长至点Q,使得 , 连接A , 请根据题意画出图形.
(1)、求图中阴影部分的面积(用含m和n的式子表示);(2)、若 , , 求阴影部分的面积.23.(1)、【操作与探究】如图1,正方形中,点E、F分别是上一点.延长至点Q,使得 , 连接A , 请根据题意画出图形.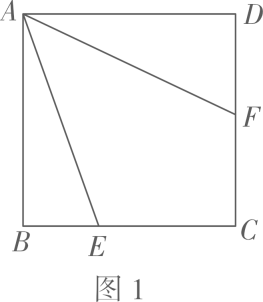
①求证:;
②若 , , 求正方形的边长AB.
(2)、【迁移与应用】如图2,正方形中,点E在边上(不与端点重合),F、G分别是上一点,交于点M, , 若 , 直接写出的值:. 24. 在平面直角坐标系中,已知点A是x轴负半轴上一点,B点是y轴正半轴上一点,将线段绕A点顺时针旋转90°,得到线段 , 连接交x轴于一点P.
24. 在平面直角坐标系中,已知点A是x轴负半轴上一点,B点是y轴正半轴上一点,将线段绕A点顺时针旋转90°,得到线段 , 连接交x轴于一点P. (1)、如图1,试判断线段之间的数量关系,并证明你的结论;(2)、如图2,D为的中点,交于点E,若 , 求证:;(3)、已知 , 在(2)的条件下,请求出点C的坐标.
(1)、如图1,试判断线段之间的数量关系,并证明你的结论;(2)、如图2,D为的中点,交于点E,若 , 求证:;(3)、已知 , 在(2)的条件下,请求出点C的坐标.