江苏省镇江市丹徒区2022-2023学年九年级下学期3月月考数学试题
试卷更新日期:2023-04-28 类型:月考试卷
一、单选题
-
1. 一组数据:2,﹣1,0,3,﹣3,2.则这组数据的中位数和众数分别是( )A、0,2 B、1.5,2 C、1,2 D、1,32. 如图,点A,B,C,D四点均在圆O上,∠AOD=68°,AO//DC,则∠B的度数为( )
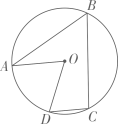 A、40° B、60° C、56° D、68°3. 据报道,人类首张黑洞照片于北京时间2019年4月10日子全球六地同步发布,该黑洞位于室女座一个巨椭圆星系的中心,距离地球5500万光年.其中5500万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、a2+a3=a5 B、(-2x2y)3=-6x6y3 C、(a-b)(-a-b)=a2-b2 D、2x2(- xy)=- x3y5. 若a+2b=8,3a+4b=18,则a+b的值为( )A、10 B、26 C、5 D、136. 我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有 人, 辆车,则可列方程组为( )A、 B、 C、 D、7. 关于x的二次函数在y轴右侧y随x的增大而减小,则a的范围为( )A、 B、 C、 D、8. 如图,C是线段AB上一动点,△ACD,△CBE都是等边三角形,M,N分别是CD,BE的中点,若AB=4,则线段MN的最小值为( )
A、40° B、60° C、56° D、68°3. 据报道,人类首张黑洞照片于北京时间2019年4月10日子全球六地同步发布,该黑洞位于室女座一个巨椭圆星系的中心,距离地球5500万光年.其中5500万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、a2+a3=a5 B、(-2x2y)3=-6x6y3 C、(a-b)(-a-b)=a2-b2 D、2x2(- xy)=- x3y5. 若a+2b=8,3a+4b=18,则a+b的值为( )A、10 B、26 C、5 D、136. 我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有 人, 辆车,则可列方程组为( )A、 B、 C、 D、7. 关于x的二次函数在y轴右侧y随x的增大而减小,则a的范围为( )A、 B、 C、 D、8. 如图,C是线段AB上一动点,△ACD,△CBE都是等边三角形,M,N分别是CD,BE的中点,若AB=4,则线段MN的最小值为( )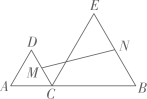 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
9. 的平方根为10. 若式子 有意义,则x的取值范围为.11. 因式分解: .12. 在数轴上表示实数a的点如图所示,化简+|a-2|的结果为.
 13. 已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a﹣b﹣2的值等于 .14. 一个圆锥的底面半径为 , 其侧面展开图的圆心角为 , 则该圆锥的侧面积为.15. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.16. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为.
13. 已知点P(a,b)在一次函数y=4x+3的图象上,则代数式4a﹣b﹣2的值等于 .14. 一个圆锥的底面半径为 , 其侧面展开图的圆心角为 , 则该圆锥的侧面积为.15. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.16. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为.
三、解答题
-
17. 计算:(1)、;(2)、18. 先化简 , 然后从的范围内选一个你喜欢的整数作为的值代入求值.19. 解方程:(1)、(2)、解方程:20.(1)、求不等式的非负整数解(2)、解不等式组:21. 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.

根据以上信息,回答下列问题:
(1)、本次调查的样本容量是 , 扇形统计图中表示A等级的扇形圆心角为;(2)、补全条形统计图;(3)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.22. 以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上. (1)、在图①中,.(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、在图①中,.(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.①如图②,在上找一点P,使.
②如图③,在上找一点P,使.
23. 已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径. (1)、求证:AE与⊙O相切;(2)、当BC=6,cosC= , 求⊙O的直径.24. 在今年新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.5元,且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同,(1)、A、B两种型号口罩的单价各是多少元?(2)、根据疫情发展情况,该公司还需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3800元,则增加购买A型口罩的数量最多是多少个?25. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线.为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为 , 房屋的顶层横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , )
(1)、求证:AE与⊙O相切;(2)、当BC=6,cosC= , 求⊙O的直径.24. 在今年新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.5元,且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同,(1)、A、B两种型号口罩的单价各是多少元?(2)、根据疫情发展情况,该公司还需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3800元,则增加购买A型口罩的数量最多是多少个?25. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线.为了测量房屋的高度,在地面上点测得屋顶的仰角为 , 此时地面上点、屋檐上点、屋顶上点三点恰好共线,继续向房屋方向走到达点时,又测得屋檐点的仰角为 , 房屋的顶层横梁 , , 交于点(点 , , 在同一水平线上).(参考数据: , , , ) (1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到1m).26. 如图,抛物线与x轴交于A、B两点(点A在点B左边),与y轴交于C,直线经过B、C两点.
(1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到1m).26. 如图,抛物线与x轴交于A、B两点(点A在点B左边),与y轴交于C,直线经过B、C两点.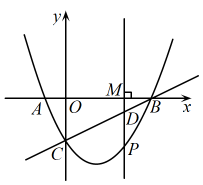 (1)、求抛物线的解析式;(2)、点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线及x轴分别交于点D、M.设 , 点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外),请直接写出符合条件的m的值.27. 如图
(1)、求抛物线的解析式;(2)、点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线及x轴分别交于点D、M.设 , 点P在抛物线上运动,若P、D、M三点中恰有一点是其它两点所连线段的中点(三点重合除外),请直接写出符合条件的m的值.27. 如图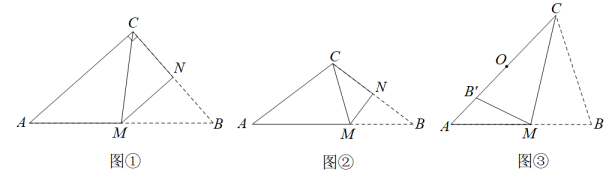 (1)、[基础巩固]如图①,在三角形纸片ABC中, , 将折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为;(2)、[思维提高]如图②,在三角形纸片ABC中, , , 将折叠,使点B与点C重合,折痕为MN,求的值;(3)、[拓展延伸]如图③,在三角形纸片ABC中, , , , 将沿过顶点C的直线折叠,使点B落在边AC上的点处,折痕为CM.求线段AC的长;
(1)、[基础巩固]如图①,在三角形纸片ABC中, , 将折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为;(2)、[思维提高]如图②,在三角形纸片ABC中, , , 将折叠,使点B与点C重合,折痕为MN,求的值;(3)、[拓展延伸]如图③,在三角形纸片ABC中, , , , 将沿过顶点C的直线折叠,使点B落在边AC上的点处,折痕为CM.求线段AC的长;