江苏省扬州市江都区邵樊片区2022-2023学年九年级下学期第一次质量检测数学试卷
试卷更新日期:2023-04-28 类型:月考试卷
一、单选题
-
1. 下列函数是二次函数的是( )A、y=2x B、 C、 D、2. 已知点P到圆心O的距离为5,若点P在圆内,则的半径可能为( )A、3 B、4 C、5 D、63. 一组数据5,8,8,10,1
 中,最后一个两位数的个位数字被墨迹覆盖,则这组数据不受影响的统计量是( ) A、平均数 B、中位数 C、众数 D、极差4. 如图, , 则下列比例式成立的是( )
中,最后一个两位数的个位数字被墨迹覆盖,则这组数据不受影响的统计量是( ) A、平均数 B、中位数 C、众数 D、极差4. 如图, , 则下列比例式成立的是( )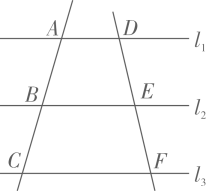 A、 B、 C、 D、5. 二次函数y=(x+2)2-3的顶点坐标是( )A、(﹣2,3) B、(2,3) C、(﹣2,﹣3) D、(2,﹣3)6. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
A、 B、 C、 D、5. 二次函数y=(x+2)2-3的顶点坐标是( )A、(﹣2,3) B、(2,3) C、(﹣2,﹣3) D、(2,﹣3)6. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )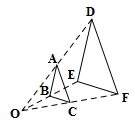 A、1∶2 B、1∶3 C、1∶4 D、1∶57. 在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )A、45° B、75° C、105° D、120°8. 如图,在平面直角坐标系中,已知A(-2,4)、P(-1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°,M为BC的中点,则PM的最小值为( )
A、1∶2 B、1∶3 C、1∶4 D、1∶57. 在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )A、45° B、75° C、105° D、120°8. 如图,在平面直角坐标系中,已知A(-2,4)、P(-1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°,M为BC的中点,则PM的最小值为( )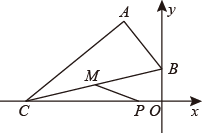 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若关于x的一元二次方程的一个根为1,则k的值为.10. 已知一组数据 , , 5,7,这组数据的极差是.11. 一个不透明的袋子中装有9个小球,其中6个红球、3个绿球,这些小球除颜色外无其他差别.从袋子中随机摸出一个小球,则摸出的小球是绿球的概率是.12. 若圆锥的底面半径为3cm,高为4cm,则它的侧面展开图的面积为cm2 .13. 将抛物线向左平移2个单位,则平移后的抛物线的函数表达式为.14. 已知线段a、b、c,其中c是a、b的比例中项,若a =9cm,b=4cm,则线段c=.15. 已知C是线段AB的黄金分割点, , 若 , 则的长为.(结果保留根号)16. 如图,抛物线y=ax2+c与直线y=kx+b交于A(-1,m),B(2,n)两点,则不等式ax2-kx+c<b的解集是.
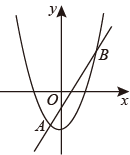 17. 如图平面直角坐标系中,⊙O的半径5 , 弦AB的长为4,过点O作OC⊥AB于点C,⊙O内一点D的坐标为(-4,3),当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是.
17. 如图平面直角坐标系中,⊙O的半径5 , 弦AB的长为4,过点O作OC⊥AB于点C,⊙O内一点D的坐标为(-4,3),当弦AB绕点O顺时针旋转时,点D到AB的距离的最小值是.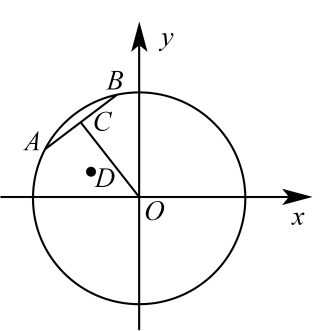 18. 在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是.
18. 在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是.三、解答题
-
19.(1)、解方程:;(2)、计算:.20. 已知O是坐标原点,的坐标分别为.
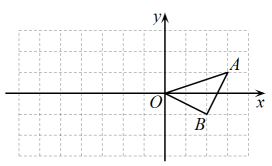
⑴画出绕点O顺时针旋转后得到的 , 并写出的坐标为 ▲ ;
⑵在y轴的左侧以O为位似中心作的位似图形 , 使新图与原图相似比为;
⑶若点在线段上,直接写出变化(2)后点D的对应点的坐标为 ▲ .21. 某校为了强化学生的环保意识,校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,复赛成绩如图所示.根据以上信息解答下列问题:
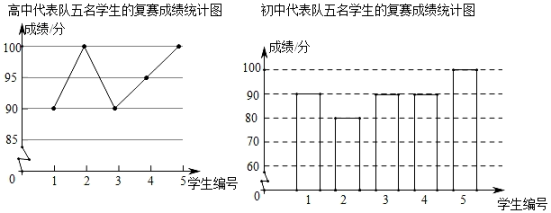 (1)、高中代表队五名学生复赛成绩的中位数为分;(2)、分别计算初中代表队、高中代表队学生复赛成绩的平均数;(3)、已知高中代表队学生复赛成绩的方差为20,请计算初中代表队学生复赛成绩的方差,并结合两队成绩的平均数和方差分析哪个队的复赛成绩较好.22. 小红和父母计划寒假期间从A、B、C、D 四个景点中随机选择景点游玩.(1)、若小红一家从中随机选择一个景点游玩,则选中C景点的概率为;(2)、若小红一家从中随机选择两个景点游玩,求选中A、C两个景点的概率.23. 在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼 , 大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为 , 已知此时高的竹竿在水平地面上的影子长 , 那么这棵大树高度是多少?
(1)、高中代表队五名学生复赛成绩的中位数为分;(2)、分别计算初中代表队、高中代表队学生复赛成绩的平均数;(3)、已知高中代表队学生复赛成绩的方差为20,请计算初中代表队学生复赛成绩的方差,并结合两队成绩的平均数和方差分析哪个队的复赛成绩较好.22. 小红和父母计划寒假期间从A、B、C、D 四个景点中随机选择景点游玩.(1)、若小红一家从中随机选择一个景点游玩,则选中C景点的概率为;(2)、若小红一家从中随机选择两个景点游玩,求选中A、C两个景点的概率.23. 在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼 , 大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为 , 已知此时高的竹竿在水平地面上的影子长 , 那么这棵大树高度是多少?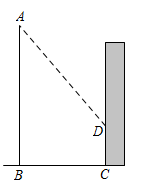 24. 如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,∠BEF=90°且CF=3FD.
24. 如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,∠BEF=90°且CF=3FD.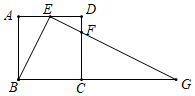 (1)、求证:△ABE∽△DEF;(2)、若AB=4,延长EF交BC的延长线于点G,求 CG的长.25. 如图, 内接于 , ,点E在直径CD的延长线上,且 .
(1)、求证:△ABE∽△DEF;(2)、若AB=4,延长EF交BC的延长线于点G,求 CG的长.25. 如图, 内接于 , ,点E在直径CD的延长线上,且 .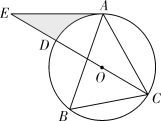 (1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.26. 六月是水蜜桃大量上市的季节,某果农在销售时发现:若水蜜桃的售价为15元/千克,则日销售量为50千克,若售价每提高1元/千克,日销售量就减少2千克,现设水蜜桃售价为x元/千克( , 且x为正整数).(1)、若某日销售量为40千克,则该日水蜜桃的单价为多少元?(2)、若政府将销售价格定为不超过30元/千克,设每日销售额为W元,求W关于x的函数表达式,并求W的最大值和最小值.27. 如图,点C是以AB为直径的半圆O内任意一点,连接AC,BC,点D在AC上,且AD=CD,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.26. 六月是水蜜桃大量上市的季节,某果农在销售时发现:若水蜜桃的售价为15元/千克,则日销售量为50千克,若售价每提高1元/千克,日销售量就减少2千克,现设水蜜桃售价为x元/千克( , 且x为正整数).(1)、若某日销售量为40千克,则该日水蜜桃的单价为多少元?(2)、若政府将销售价格定为不超过30元/千克,设每日销售额为W元,求W关于x的函数表达式,并求W的最大值和最小值.27. 如图,点C是以AB为直径的半圆O内任意一点,连接AC,BC,点D在AC上,且AD=CD,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).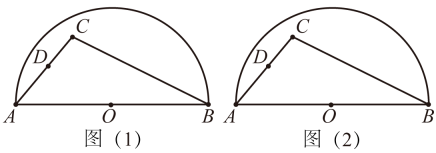 (1)、在图(1)中,画出的中线AE;(2)、在图(2)中,画出的角平分线AF.28. 如图1,在平面直角坐标中,抛物线与x轴交于点、两点,与y轴交于点C,连接BC,直线交y轴于点M.P为直线BC上方抛物线上一动点,过点P作x轴的垂线,分别交直线BC、BM于点E、F.
(1)、在图(1)中,画出的中线AE;(2)、在图(2)中,画出的角平分线AF.28. 如图1,在平面直角坐标中,抛物线与x轴交于点、两点,与y轴交于点C,连接BC,直线交y轴于点M.P为直线BC上方抛物线上一动点,过点P作x轴的垂线,分别交直线BC、BM于点E、F.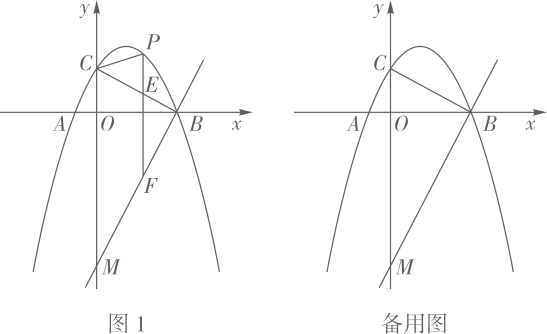 (1)、求抛物线的表达式;(2)、当点P落在抛物线的对称轴上时,求△PBC的面积;(3)、①若点N为y轴上一动点,当四边形BENF为矩形时,求点N的坐标;
(1)、求抛物线的表达式;(2)、当点P落在抛物线的对称轴上时,求△PBC的面积;(3)、①若点N为y轴上一动点,当四边形BENF为矩形时,求点N的坐标;②在①的条件下,第四象限内有一点Q,满足 , 当△QNB的周长最小时,求点Q的坐标.